Функциональная пропедевтика на уроках математики в пятых-шестых классах
Департамент
образования Тверской области
Тверской
педагогический колледж
Цикловая
методическая комиссия естественно-математических
дисциплин
по математике
ВЫПУСКНАЯ
КВАЛИФИКАЦИОННАЯ РАБОТА
по
специальности 050201 «Математика»
Тема
Функциональная
пропедевтика на уроках математики
в 5-6
классах
Выполнила: студентка
Тарасова Валентина Александровна
Оглавление
Введение
Глава
1. Психологические особенности мышления и учебной деятельности учащихся 5-6
классов
Глава
2. Функции
Глава
3. Функциональная пропедевтика
Глава
4. Анализ учебников по математике авторов Н.Я. Виленкина и Л.Г. Петерсон для 5
и 6 классов
Заключение
Введение
Проблема пропедевтики основных понятий математики возникает при
обнаружении определенных трудностей в их формировании в систематическом курсе.
Ее можно осуществлять непрерывным образом, через основное содержание учебного
материала предыдущих курсов. В этой связи возникает вопрос об организации
учебной работы на основе содержания математического образования на каждой
ступени, одним из условий ее осуществления является наличие
содержательно-логических линий в предметном курсе. Проблема логической
цельности школьной математики имеет вековую историю: в начале ХХ века
определилась тенденция к алгебраизации курса, и ныне в основе преподавания
лежит функциональный подход.
В настоящее время в обществе сложилось новое понимание основной цели
образования. Учитель в первую очередь должен заботиться о формировании у
ученика способности к саморазвитию, которая обеспечит интеграцию личности в
национальную и мировую культуру. Во главу угла при обучении математики
ставится:
а) обучение деятельности - умению ставить цели, организовать свою
деятельность, оценивать результаты своего труда;
б) формирование личностных качеств: ума, воли, чувств и эмоций,
творческих способностей, познавательных мотивов деятельности.
Функциональная линия школьного курса математики является в настоящее
время одной из ведущих, определяющих стиль изучения многих тем и разделов
курсов алгебры и начала анализа. Наиболее заметной особенностью материала этой
линии является то, что с его помощью возможно устанавливать разнообразные связи
в обучении.
В целом развитию функциональных представлений учащихся в данном курсе
содействуют: развитие понятия числа, овладение тождественными преобразованиями,
изучение методов решения уравнений, изучение неравенств и др. Поэтому учащиеся
5-6 классов приобретают достаточные представления, необходимые для успешного
изучения функции в старших классах.
Умеренная алгебраизация курса математики 5-6 классов содействует
обеспечению соответствующего данному возрасту учащихся развития логического
мышления, функциональных представлений, способностей к абстрактному мышлению,
формированию алгоритмической культуры, совершенствованию устной и письменной математической
речи, воспитанию мировоззрения, т.е. овладение учебным материалом обеспечивает
целенаправленное воспитание и развитие учащихся.
Направления подобной работы выражаются в характере задач, предлагаемых
учащимся. Материал начального математического курса содержит достаточное
количество примеров, на которых можно разъяснить зависимость одной величины от
другой. К ним, в частности, относятся: задачи на составление и решение
уравнений, оптимизационные и комбинаторные задачи, задачи с величинами, находящимися
в прямой и обратной зависимости, задачи с использованием таблиц, числовой оси и
координатной плоскости.
Таким образом, опосредованная пропедевтика предполагает постепенную
функциональную подготовку, не требующую ни специальной терминологии, ни символики;
достаточно последовательно проводить идею изменяемости окружающего мира;
взаимозависимости между величинами, используя для этой цели материал школьных
учебников. Объективные возможности для пропедевтики имеются, учитель должен их
видеть и использовать в обучении школьников.
Цель: изучить методику функциональной пропедевтики на уроках математики в 5-6
классах.
Задачи:
. Проанализировать и изучить психолого-педагогическую и методическую
литературу по теме работы.
. Рассмотреть и проанализировать основные учебники по математике 5-6
классов.
. Разработать практический и методический материал по функциональной
пропедевтике в 5-6 классах.
Объект исследования: методика преподавания математики.
Предмет исследования: функциональная пропедевтика на уроках математики в 5-6
классах.
Гипотеза: Для успешного усвоения учащимися основной школы понятия функции и
способов её задания, необходимо в 5-6 классах систематически предлагать
упражнения пропедевтического характера.
Глава 1. Психологические особенности мышления и учебной
деятельности учащихся 5-6 классов
функциональная пропедевтика математика
Человек, появляясь на свет, наделен лишь самыми элементарными механизмами
для поддержания жизни. По физическому строению, организации нервной системы, по
типам деятельности и способам ее регуляции человек - наиболее совершенное
существо в природе. Однако по состоянию в момент рождения в эволюционном ряду
заметно падение совершенства - у ребенка отсутствуют какие-либо готовые формы
поведения. Как правило, чем выше стоит живое существо в ряду животных, тем
дольше длится его детство, тем беспомощнее это существо при рождении. Таков
один из парадоксов природы, который предопределяет историю детства.
В ходе истории непрерывно росло обогащение материальной и духовной
культуры человечества. За тысячелетия человеческий опыт увеличился во много
тысяч раз. Но за это же время новорожденный ребенок практически не изменился.
Опираясь на данные антропологов об анатомо-морфологическом сходстве кроманьонца
и современного европейца, можно предположить, что новорожденный современного
человека ни в чем существенном не отличается от новорожденного, жившего десятки
тысяч лет назад.
Как же получается, что при сходных природных предпосылках уровень
психического развития, которого достигает ребенок на каждом историческом этапе
развития общества, не одинаковый? Детство - период, продолжающийся от
новорожденности до полной социальной и, следовательно, психологической
зрелости; это период становления ребенка полноценным членом человеческого
общества. При этом продолжительность детства в первобытном обществе не равна
продолжительности детства в эпоху Средневековья или в наши дни. Этапы детства
человека - продукт истории, и они столь же подвержены изменению, как и тысячи
лет назад. Поэтому нельзя изучать детство ребенка и законы его становления вне
развития человеческого общества и законов, определяющих его развитие.
Продолжительность детства находится в прямой зависимости от уровня материальной
и духовной культуры общества.
Общеизвестно, что от знаний, педагогического мастерства, активной позиции
учителя в решающей степени зависит успех модернизации системы образования. В
каких же знаниях сейчас больше всего нуждается учитель?
По убеждению многих учёных, учителя особенно нуждаются в психологических
знаниях. Ведь модернизация школы на передний план выдвигает задачу воспитания
ученика, всестороннее его развитие.
Ещё К.Д. Ушинский указывал, что если мы хотим воспитать ребёнка
всесторонне, также всесторонне его нужно изучать. Правильно изучать своих
учащихся учитель сможет, лишь глубоко зная общие закономерности развития
ребёнка, психологические закономерности развития его способностей, интересов,
склонностей и других индивидуальных личностных особенностей.
Для каждого возраста существует своя специфическая социальная ситуация
развития, т. е. определённое соотношение условий социальной сферы и внутренних
условий формирования личности. Взаимодействие внешних и внутренних факторов
порождает типичные психологические особенности, общие для людей одного
возраста.
Мышление - высшая форма отражения мозгом окружающего мира, наиболее
сложный познавательный психический процесс, свойственный только человеку.
Возможности познания окружающего мира с помощью анализаторов очень
ограничены. Человек очень мало знал бы об окружающем мире, если бы его познание
ограничивалось только теми показаниями, которые дают зрение, слух, осязание,
обоняние и некоторые другие анализаторы. Возможность глубокого и широкого
познания мира открывает человеческое мышление.
Мышление - процесс опосредованного и обобщённого познания (отражения)
окружающего мира. Сущность его в отражении: общих и существенных свойств
предметов и явлений, в том числе и таких свойств, которые не воспринимаются
непосредственно; существенных отношений и закономерных связей между предметами
и явлениями.
Мышление играет поистине огромную роль в познании. Мышление расширяет
границы познания, даёт возможность выйти за пределы непосредственного опыта
ощущений и восприятия. Мышление даёт возможность знать и судить о том, что
человек непосредственно не наблюдает, не воспринимает. Наша мысль вырывает нас
из плена непосредственной конкретной видимости и позволяет улавливать сходство
в различном и различное в сходном, позволяет открывать закономерные связи между
явлениями и событиями. Оно позволяет предвидеть наступление таких явлений,
которые в данный момент не существуют. Без преобразующей творческой работы
мысли невозможно было бы спланировать трудовые процессы, создать орудия труда,
поставить новые цели.
Мышление перерабатывает информацию, которая содержится в ощущениях и
восприятии, а результаты мыслительной работы проверяются и применяются на
практике. Мышление взрослого, нормального человека неразрывно связано с речью.
Мысль не может ни возникнуть, ни протекать, ни существовать вне языка, вне
речи. Мы мыслим словами, которые произносим вслух или проговариваем про себя,
т.е. мышление происходит в речевой форме. В речи мысль не только формулируется,
но и формируется, развивается.
Выделяют основные формы мышления: понятие, суждение, умозаключение.
Понятие - это мысль о предмете или явлении, отражающая общие и притом
существенные его свойства. В понятиях мы можем выразить то, что невозможно
представить наглядным образом. Т. е. понятие шире, чем представление. Так, нам
не удаётся мысленно увидеть фигуру, имеющую сто углов, но понятие «стоугольник»
имеется, и мы знаем, что практически эта фигура может существовать.
Мысли о предметах и явлениях, о связях и отношениях между ними мы
выражаем в форме суждений.
Суждение - форма мышления, в которой содержится утверждение или отрицание
чего-либо. На основе одного или нескольких суждений, делается какой-либо вывод.
Форма мышления, в которой из одного или нескольких суждений выводится новое
суждение, называется умозаключением. Примером умозаключений могут быть
доказательства теорем по геометрии.
Умозаключения бывают индуктивные и дедуктивные.
Индуктивные умозаключения (индукция) - способ рассуждения, при котором на
основе ряда отдельных фактов (выраженных в частных суждениях) делается вывод,
высказывается общее суждение.
Дедуктивные умозаключения (дедукция) - способ рассуждения, при котором от
общих положений идут к частным выводам. Процесс мышления, в котором
умозаключения строго основываются на правильных суждениях, называется
логическим мышлением. Ярким примером строго логического мышления являются
доказательства теорем в геометрии и другие математические выводы, где всё
последующее основано на предыдущих положениях, одно неизбежно вытекает из
другого.
Учащимся 5-6 классов соответствует возраст 11-12 лет, который явля-ется
подростковым. Этот период принято считать переходным возрастом, он является
сложным для школьников.
В то же время наблюдаются и повышенная утомляемость подростков. Утомление
обычно развивается в две фазы: первая - двигательное беспокойство, вторая -
сонливость, дремота или, наоборот, сильное возбуждение. Ко всему этому следует
добавить и отклонения, связанные с усиленным ростом. В основе их лежат две
причины: первая - нарушение содружественной работы отдельных органов, вторая -
дефицит различных веществ, необходимых интенсивно развивающемуся и растущему
организму. Отсюда - головокружение, потемнение в глазах и даже обморок при
резком изменении положения тела, длительном неподвижном состоянии. Дело в том,
что регуляторная система, поддерживающая постоянное артериальное давление при
любых изменениях положение тела у подростков, временно отстаёт в своём развитии
от слишком быстрого увеличения продольных размеров тела и поэтому срабатывает с
опозданием. Вторая причина ведёт к нарушению осанки, к искривлению позвоночника
и т.д.
Со всеми этими особенностями связана успеваемость. С одной стороны,
непрерывно возрастают возможности в учебно-познавательной деятельности,
совершенствуются память, внимание, качественно преобразуется характер мышления,
развиваются критические черты характера, растёт самостоятельность и активность
школьников, расширяется круг их интересов, стремлений, хотя некоторые причины
делают процесс нарастания учебных возможностей менее интенсивным, чем в
предшествующей и последующей возрастных группах.
Но именно в этот период существует возможность оказать нужное
педагогическое влияние, потому что вследствие "недостаточной обобщенности
нравственного опыта" нравственные убеждений, подростка находятся еще в
неустойчивом состоянии.
Нравственные убеждения возникают и оформляются только переходном
возрасте, хотя основа для их возникновения был заложена гораздо раньше. В
убеждении, по мнению Л.И. Божович находит свое выражение более широкий
жизненный опыт школьника, проанализированный и обобщенный с точки зрения
нравственных норм, и убеждения становятся специфичными мотивам поведения и
деятельности школьников.
Одновременно с развитием убеждений формируется нравственное
мировоззрение, которое представляет собой систему убеждений что приводит к
качественным сдвигам во всей системе потребностей и стремлений подростка.
Под влиянием развивающегося мировоззрения происходит иерархизация в
системе побуждений, в которой ведущее место начинают занимать нравственные
мотивы.
Установление такой иерархии приводит к стабилизации качеств личности,
определяя ее направленность, и "позволяет человеку в каждой конкретной
ситуации занять свойственную ему нравственную позицию".
У детей 11-12 лет резко возрастает познавательная активность и
любознательность. Всё, что выходит за рамки повседневной жизни ребёнка, -
проблемы жизни и смерти, войны и мира, экологические и социальные темы, способы
познания мира, ведьмы и гороскопы, НЛО и инопланетяне - всё это занимает в
сознании шестиклассника большое место. Эти проявления любознательности
поверхностны и разбросаны и совершенно не связаны со школьной программой. Всё
это происходит потому, что подросток ощущает свои силы и возможности,
взрослеет. Значение интересов в подростковом возрасте чрезвычайно велико. По их
содержанию можно судить о развитии личности ребёнка.
Если же у ребёнка полностью отсутствуют какие-либо увлечения, то, скорее
всего, их не было у окружающих взрослых. Бывает наоборот: родители слишком
активно стараются развить какой-либо интерес у школьника, что ведёт к обратному
результату.
Играет роль в отсутствии интересов и социальная обстановка, нехватка
кружков, бедность библиотеки, отсутствие спортивных секций и недостаточная
материальная обеспеченность родителей.
Большое влияние на развитие интересов в подростковом возрасте оказывает
общая атмосфера школы: если педагоги увлечены своим предметом, имеют большой
круг интересов, желают всё это передать ученикам - всё это служит поддержкой
влечения школьников.
Иногда сталкиваясь с первым неуспехом (или небольшим успехом), подросток
быстро гаснет из-за неуверенности в себе. Родители в такой ситуации должны
поддержать подростка, укрепить его самооценку, проанализировав причины неудач.
Часто отсутствие интересов отмечается у подростков с ярко выраженной
тенденцией к «отказу от усилий». Дети готовы пойти за любым, кто покажет им,
как можно, не прилагая никаких усилий, развлечь себя и чем-то заняться. Эти
ребята - первые кандидаты в асоциальные группы. Они нуждаются в особом внимании
и родителей и педагогов. Таким образом, чаще всего интересы шестиклассников
лежат вне школы. А это, в свою очередь, часто ведёт к ухудшению успеваемости.
Переход от детства к юности присутствует во всём развитии подростка: его
анатомо-физиологическом состоянии, интеллектуальном, нравственном состоянии и
всех видах его деятельности. В подростковом возрасте серьёзно изменяются
условия жизни и деятельности школьника, что приводит к перестройке психики,
изменении уже сложившихся взаимоотношений с людьми. Особое значение имеют
чувства, они становятся преднамеренными, сильными, осмысленными. Проявляются
очень бурно, особенно гнев, иногда аффектно. Это период тяжёлого кризиса,
”катастроф” (упрямство, эгоизм, замкнутость и т.д.). Важно бережно относиться к
духовному миру подростков, проявлению их чувств. Проблемой в этом возрасте
является несогласованность убеждений, моральных идей и понятий с одной стороны,
поступков и действий с другой. Педагог должен глубоко осмыслить особенности
развития подростков, уметь поставить себя на их место. Дети в этом возрасте
способны понять аргументацию, убедиться в её обоснованности, согласиться с
разумными доводами.
Существует ещё одна причина трудностей в бучении в средних классах. Это
формализм в учёбе. Различают два вида формализма:
. Школьники, как правило, не пытаются проникнуть в суть того, что они
изучают, а механически, не задумываясь, без осмысления, зазубривают написанное
в учебнике или сказанное учителем. Такой вид формализма часто наблюдается у
прилежных подростков, желающих хорошо учиться, но не умеющих правильно мыслить
и чем-то интересоваться.
. Школьники легко оперируют абстрактными понятиями, владеют способами
теоретического мышления, но испытывают трудности «в восхождении к конкретному».
Основная причина такая же - низкий уровень развития познавательной потребности,
отсутствие стремления понять суть явлений действительности, понять реально
существующие причинно-следственные связи.
Формальное усвоение школьных знаний отрицательно влияет не только на их
качество, но и на развитие личности ребёнка. При наличии формализма первого
вида может возникнуть учебная перегрузка, что проводит к повышенной
утомляемости.
В подростковом возрасте существенно перестраивается характер учебной
деятельности. В 5 классе школьники переходят к систематическому изучению основ
наук. Причём не только усложняется сама учебная деятельность: увеличивается
количество учебных предметов, вместо одного учителя с классом работают
пять-шесть учителей, у которых разные требования, разный стиль ведения урока,
разное отношение к учащимся. Главное, постепенно нарастающая взрослость
подростка делает неприемлемыми для него привычные младшему школьнику старые
формы и методы обучения. Если ученик ещё недавно охотно слушал подробные
объяснения учителя, то теперь подобная форма знакомства с новым материалом
часто вызывает у учащегося скуку, равнодушие, явно тяготит его. Склонный ранее
к дословному воспроизведению учебного материала, он стремится теперь излагать
его своими словами и протестует, когда учитель требует точного воспроизведения
(Формулы, закона, определения).
Расширение связей с окружающим миром, широкое всепоглощающее общение со
сверстниками, личные интересы и увлечения также часто снижают непосредственный
интерес подростков к учению. Сознательно-положительное отношение ребят к учению
возникает тогда, когда учение удовлетворяет их познавательные потребности,
благодаря чему знания приобретают для них определённый смысл как необходимое и
важное условие подготовки к будущей самостоятельной жизни. Однако здесь порой
наблюдается расхождение: стремление к приобретению знаний может сочетаться с
безразличным или даже отрицательным отношением к школьному обучению. Это может
быть своеобразной реакцией на те или иные неудачи в учении, на конфликт с
учителем. Подросток обычно остро переживает учебные неудачи и из-за самолюбия
иногда маскирует подлинное отношение к этим неудачам: делает вид, что к успехам
в учении он совершенно безразличен и равнодушен.
Наиболее существенную роль в формировании положительного отношения
подростка к учению играют идейно-научная содержательность учебного материала,
его связь с жизнью и практикой, проблемный и эмоциональный характер изложения,
организация поисковой познавательной деятельности, дающей учащимся возможность
переживать радость самостоятельных открытий, вооружение подростков
рациональными приёмами учебной работы, навыками самовоспитания, являющимися
непременной предпосылкой для достижения успеха.
В процессе учения очень заметно совершенствуется мышление подростка.
Содержание и логика изучаемых в школе предметов, изменение характера и форм
учебной деятельности формируют и развивают у него способность активно,
самостоятельно мыслить, рассуждать, сравнивать, делать глубокие обобщения и
выводы. Доверие учителя к умственным возможностям подростка как нельзя больше
соответствует возрастным особенностям его личности.
Основная особенность мыслительной деятельности подростка - нарастающая с
каждым годом способность к абстрактному мышлению, изменение соотношения между
конкретно-образным и абстрактным мышлением в пользу последнего.
Конкретно-образные (наглядные) компоненты мышления не исчезают, а сохраняются и
развиваются, продолжая играть существенную роль в общей структуре мышления
(например, развивается способность к конкретизации, иллюстрированию, раскрытию
содержания понятия в конкретных образах и представлениях). Поэтому при
однообразии, односторонности или ограниченности наглядного опыта тормозится
вычленение абстрактных существенных признаков объекта. Так, например, младшие
подростки иногда не узнают прямоугольного треугольника при положении прямого
угла вверху, когда гипотенуза является основанием треугольника, путаются в
хорошо знакомом им доказательстве при необычном построении чертежа.
Значение конкретно-образных компонентов мышления сказывается и в том, что
в ряде случаев воздействие непосредственных чувственных впечатлений оказывается
сильнее воздействия слов (текста учебника, объяснения учителя). В результате
происходит неправомерное сужение или расширение того или иного понятия, когда в
его состав привносятся яркие, но несущественные признаки, случайно
запечатлевшиеся иллюстрации в учебнике, наглядном пособии, кадры учебного
кинофильма.
В процессе учения подросток приобретает способность к сложному
аналитико-синтетическому восприятию (наблюдению) предметов и явлений. Восприятие
становится плановым, последовательным и всесторонним. Подросток воспринимает
уже не только то, что лежит на поверхности явлений, хотя здесь многое зависит
от его отношения к воспринимаемому объекту. Отсутствие интереса, равнодушие к
материалу - и ученик поражает поверхностностью, легковесностью своего
восприятия. Подросток может добросовестно смотреть и слушать, но восприятие его
будет случайным.
Существенные изменения в подростковом возрасте претерпевают память и
внимание. Развитие идет по пути усиления их произвольности. Нарастает умение
организовывать и контролировать свое внимание, процессы памяти, управлять ими.
Память и внимание постепенно приобретают характер организованных, регулируемых
и управляемых процессов.
В подростковом возрасте замечается значительный прогресс в запоминании
словесного и абстрактного материала. Умение организовать мыслительную работу по
запоминанию определенного материала, умение использовать специальные способы
запоминания развито у подростков в гораздо большей степени, чем у младших
школьников.
Развитие внимания отличается известной противоречивостью: с одной
стороны, в подростковом возрасте формируется устойчивое, произвольное внимание,
с другой - обилие впечатлений, переживаний, бурная активность и импульсивность
подростка часто приводят к неустойчивости внимания, его быстрой отвлекаемости.
Невнимательный и рассеянный на одном уроке («нелюбимом»), ученик может
собранно, сосредоточенно, совершенно не отвлекаясь, работать на другом
(«любимом») уроке.
Лучший способ организовать внимание подростка связан не с применением
учителем каких-либо особых приемов, а с умением так организовать учебную
деятельность, чтобы у ученика не было ни времени, ни желания, ни возможности
отвлекаться на длительное время. Интересное дело, интересный урок способны
захватить подростка, и он с увлечением работает весьма продолжительное время,
не отвлекаясь. Активная познавательная деятельность - вот что делает урок
интересным для подростка, вот что само по себе способствует организации его
внимания. Интересная работа мысли вызывает чувство удовлетворения, а вместе с
тем - стремление во что бы то ни стало довести работу до конца. Положительные
эмоции обладают созидающей силой. Скука тоже эмоция, но она не обогащает
умственную деятельность, а подавляет её.
Нередко в классе несколько человек хорошо усваивают полученную информацию
только при определенном способе ее подачи: аудиальном, визуальном или
кинестетическом. Но если учитель переходит на другую модальность, ученику
приходится транслировать информацию в свою. Отключаясь, временно, от
действительности, ученик не слышит объяснение учителя, в результате чего у
учащегося появляются пробелы в знаниях, что выясняется чаще всего только при
проверке. Следовательно, немаловажным является внимательное отношение к ведущей
модальности ученика.
Восприятие школьником учебной информации зависит и от его субъектного
опыта, который приобретается через общение в семье, со сверстниками, через
различные источники информации и в рамках целенаправленного обучения. Любую
информацию ребенок переводит на свой язык на основе этого опыта. В результате у
ученика складывается собственная система знаний, которая представляет целостную
психическую структуру. Значит, новая информация должна согласовываться с уже
сформированными у ребенка представлениями, житейскими понятиями, ценностями,
эмоциональными кодами, способами переработки информации, составляющими
субъектный опыт ученика. Но не всегда житейское понятие совпадает с научным,
что может быть причиной неадекватного восприятия школьником учебного материала.
Поэтому важно раскрыть субъектный опыт ученика, то есть выявить, какой смысл он
вкладывает в изучаемое понятие, и скорректировать субъектный опыт школьника с
общественно-историческим.
Таким образом, при обучении важно учитывать не только
психофизиологические особенности школьника, но и его субъектный опыт, который
справедливо отнести к социальным явлениям.
Введение нового учебного материала с учетом преобладания у одних учащихся
образного мышления, а у других - аналитического требует организации условий, в
которых активизируются как образные, так и аналитические компоненты мышления.
Это условие является базовым при введении учебного материала. На этой основе, с
целью обеспечения восприятия полученной информации учениками с разными
познавательными стилями, необходимо представить ее с учетом всех, по
возможности, каналов восприятия. При этом для формирования личностно значимых
знаний, как при восприятии нового материала, так и при его усвоении необходимо
обеспечить связь с субъектным опытом учащихся. Реализация этих условий
предполагает создание целостного представления об изучаемом материале на
подготовительном и основном этапах работы с теоретическим материалом. Эта
целостность должна отражать связи между новыми и полученными ранее в разных
школьных дисциплинах и в обыденной жизни знаниями, и представлена в разной
форме, с учетом разных познавательных стилей.
Но если восприятие новой информации должно происходить в стиле,
соответствующем стилю ученика, то на последующих этапах при закреплении
полученных знаний с целью развития стилевой гибкости необходимо обеспечить
деятельность, направленную на активизацию неприоритетных для данного ученика
компонентов мышления и недоминирующего канала восприятия. Это требует
определенной организации работы с математическими задачами на этапе закрепления
работы с учебным материалом.
По мнению ведущих психологов, если есть условия, способности развиваются,
то есть способности развиваются в деятельности. Мы, педагоги, должны создать
для учащихся условия и предоставить возможности проявить себя в различной
деятельности, а также проследить, как под влиянием социально - культурной среды
происходит развитие личности ребенка.
Из вышесказанного следует:
.) В процессе обучения математике необходимо учитывать индивидуальные
особенности школьников, в том числе психофизиологические особенности и
субъектный опыт.
.) В методике обучения математике практически нет работ описывающих
способы учета психофизиологических особенностей учащихся при построении
учебного процесса.
Глава 2. Функции
.1 Понятие функции. Способы задания функции
функциональная пропедевтика математика
Введение в понятия функции - это длительный процесс, завершающийся
формированием представлений о всех компонентах этого понятия в их взаимной связи
и о роли, играемой им в математике и в её приложениях. Этот процесс ведётся по
трём основным направлениям:
упорядочение имеющихся представлений о функции, развёртывание системы
понятий, характерных для функциональной линии (способы задания и общие свойства
функций, графическое истолкование области определения, области значений,
возрастания и т.д. на основе метода координат);
глубокое изучение отдельных функций и их классов;
расширение области приложений алгебры за счёт включения в неё идеи
функции и разветвлённой системы действий с функцией.
Первоначально понятие функции как аналитического выражения сложилось в
первой половине XVIII века в связи с бурным развитием производительных сил.
Термин функция ввёл И. Бернулли в 1718 году. Л. Эйлер предложил в 1748 году
определение функции как аналитического выражения.
В общем виде определение функции было дано Н.И. Лобачевским в 1834 году.
В современной формулировке: «Если каждому допустимому значению переменной
величины х соответствует определённое значение переменной величины у, то х
называется независимой переменной, а у - функцией от х».
В этой формулировке слово «соответствует» не говорит о виде зависимости
переменных величин. Оно может быть задано описанием; например, чтобы находить
последовательные цифры при извлечении квадратного корня из положительного
числа, имеется определённый алгоритм.
Идея функциональной зависимости находит свое отражение не только в
математике, но и в ряде других наук - физике, химии, биологии, медицине,
истории, кибернетике. Велика роль функции как мощного аппарата в познании
процессов, происходящих в реальном мире. Знание функциональных зависимостей
помогает найти ответы на разнообразные вопросы - от расшифровки памятников
древности до управления сложнейшими производственными процессами. Наблюдая
веками явления природы, человек замечал соответствие между ними. Систематизируя
и обобщая устойчивые взаимосвязи в природе, он познал закономерности и учился
применять их для объяснения разнообразных явлений природы. Математическими
моделями таких закономерностей и являются функции.
Понятия соответствия и однозначного аналитического выражения функции не
противопоставляются, второе просто частный случай первого.
Соответственно можно к понятию функции подвести:
) рассматривая однозначные аналитические выражения зависимостей;
) дав примеры соответствия между величинами, не записанными аналитически.
I. Из алгебры аналитические выражения зависимостей у=ах, у=а/х,
у=ах+в и другие; из геометрии - формулы площадей и объёмов, в которых
зависимость задана тоже аналитически.
II. Рассмотрим зависимости, заданные не аналитически. Например,
можно взять результат наблюдения температуры воздуха:
часов: -2о
часов: 0о
8 часов: +1о
9 часов: +1,5о
10 часов: +3о
11 часов: +5о
12 часов: +6,5о
13 часов: +7,5о
14 часов: +8о
15 часов: +8,6о
16 часов: +7о
17 часов: +5о
Рассматривая пары значений времени и температуры и устанавливают, что
каждому значению времени наблюдения соответствует определённое значение
температуры. В данном случае температура - функция времени.
Понятие функции является одним из понятий, отражающих взаимосвязи явлений
и предметов. Это одно из важнейших понятий математики, исходное понятие ведущей
её области - математического анализа.
Определение: Функцией называется такая зависимость переменной y от переменной x, при которой каждому значению x соответствует единственное значение y.
Переменную x называют независимой переменной или аргументом, а y -
зависимой переменной. Говорят также, что y является функцией от x. Значение y,
соответствующее заданному значению x, называют значением функции.
Чтобы задать функцию, нужно задать числовое множество Х (его называют
областью определения функции) и способ (правило), с помощью которого для
каждого числа x из множества Х можно найти соответствующее число у - значение
функции.
Функции принято обозначать буквами f, g, h и др. Если f - функция, то значение переменной у, соответствующее
аргументу х, обозначают f(x), т.е. y=f(x).
Чаще всего функции задают с помощью формул, указывающих, как по данному
значению аргумента найти соответствующее значение функции. Например, если длина
стороны квадрата равна x дм, а площадь y дм2 , то формула y=x2 задаёт функцию, областью определения
которой будет множество положительных действительных чисел.
Если куплено х тетрадей, по 3 рубля каждая, а у рублей - стоимость всей
покупки, то формула у=3х задаёт функцию, область определения которой есть
множество целых неотрицательных чисел.
Иногда функцию задают таким образом:
у= 3х-1, при х>0;
х, при х≤0,
т. е. на разных участках значений х функция задаётся различными
формулами.
Часто при задании функции с помощью формулы её область определения не
указывается. В таких случаях считают, что область определения состоит из всех
значений переменной, при которой эта формула имеет смысл. Никогда не следует
забывать, что формула - это не сама функция, а лишь один из способов её
задания. Следует отметить, что функцию можно задать и просто описанием.
Например: каждому числу х поставить в соответствие его целую часть, т. е.
у=[х].
Иногда функцию задают в виде таблицы. Примером табличного задания функции
будет зависимость точки кипения воды от атмосферного давления:
|
Давление (мм)
|
300
|
350
|
400
|
450
|
500
|
550
|
600
|
650
|
700
|
|
Температура (°С)
|
75,8
|
79,6
|
83,0
|
85,8
|
88,5
|
91,2
|
93,5
|
95,7
|
97,6
|
Приведём ещё пример зависимости длины пружины от растягивающей её силы
(данные получены эмпирическим путём):
|
Растягивающая сила (кг)
|
0
|
5
|
10
|
15
|
20
|
25
|
|
Длина пружины (см)
|
13,0
|
14,2
|
15,4
|
16,6
|
17,8
|
19,0
|
При табличном задании функции можно находить и промежуточные значения
переменных с помощью линейного интерполирования, но приближённо.
Многие приборы записывают непрерывно показания графически, например,
термографы, барографы, сейсмографы, кардиографы и др.
В качества примера хорошо продемонстрировать учащимся запись барографа
или термографа.
На рисунке дан график изменения давления с 0 часов ночи до 12 часов дня:
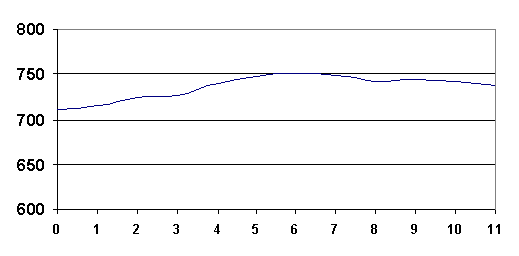
На
следующем графике дана зависимость между скоростью автомобиля «Победа» и
наименьшим временем, необходимым для достижения этой скорости:
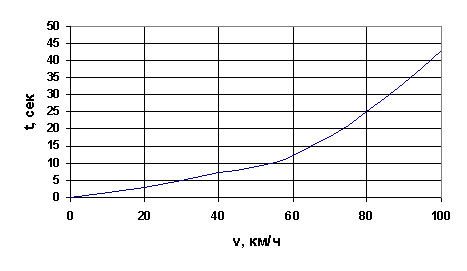
Способы
задания функции воспринимаются разрозненно, учащиеся не допускают мысли, что
одна и та же функция может быть задана различными способами. Разные способы
задания функции обладают своими преимуществами и недостатками. Так, если
функция задана аналитически, удобно находить значение функции при любом
значении аргумента из области определения, исследовать её свойства, но нет
наглядности, которую даёт графический способ задания. В то же время наглядный
графический способ задания имеет существенный недостаток - приблизительность в
нахождении значений функции. Табличный способ избавляет от вычислений, но он
тоже не нагляден, и таблица даёт только некоторые значения функции. Поэтому,
как правило, при изучении функциональных зависимостей пользуются всеми
способами задания этих зависимостей.
Учащиеся
«не видят» функцию, если она задана неявно. Функция называется неявно заданной,
или неявной, если её связь с аргументом задана с помощью уравнения, не
решённого относительно функции.
Например:
3х-у+1=0, ху=5.
Иногда
для неявной функции можно получить её явное задание. Это можно сделать тогда,
когда уравнение, связывающее аргумент и функцию, удаётся решить относительно
функции:
5х-3+2у=0,
у=3-5х,
у=(3-5х)/2.
Чтобы подготовить учеников к сознательному усвоению идеи функциональной
зависимости, понятий функции и уравнения в VII и более старших классах школы,
необходимо заранее и постепенно подготовить их к знакомству с этими понятиями.
Глава 3. Функциональная пропедевтика
.1 Общие сведения
ПРОПЕДЕВТИКА (от греч. propaideuo - предварительно обучаю), введение в
какую-либо науку, предварительный вводный курс, систематически изложенный в
сжатой и элементарной форме.
В дидактике под пропедевтикой вообще понимают подготовительный курс,
представляющий введение в какую-либо науку или учебный предмет и отличающийся
элементарной формой изложения.
Вопрос о пропедевтике возникает тогда, когда
обнаруживаются определенные трудности в формировании некоторых понятий или при
слишком компактном изложении конкретной темы, что влечет за собой
целесообразность распределения материала на больший промежуток времени. Если
сделать это с выделением начального концентра, то получится пропедевтический
курс, можно же осуществить подобное действие непрерывным образом, распределяя
часть материала по другим темам, то есть опосредованно, через основное
содержание учебного материала.
Очевидно, что одним из важнейших условий осуществления
опосредованной пропедевтической работы является идейная стройность школьного
курса математики, наличие логической связи между элементарной и высшей
математикой.
Проблема логической цельности школьного курса
математики имеет вековую историю. К концу 19 века сложилась международная
традиционная система математического образования, которая характеризовалась
оторванностью от высшей математики и вообще науки математики, разделением
элементарной математики на 4 учебных предмета: арифметику, алгебру, геометрию,
тригонометрию, существующих самостоятельно и независимо друг от друга. Во
многих странах мира прогрессивные математики и педагоги выступали с критикой
данной системы обучения и с позитивными предложениями по реформе
математического образования. В 1897 году в Цюрихе на I Международном конгрессе математиков выступил с докладом
известный геометр, педагог высшей немецкой школы Феликс Клейн, в котором
содержалась мысль о том, что в математике средней школы «функциональная идея»
должна быть центральной: «Руководящую роль в школьном курсе математики должно
играть понятие функции. Оно должно быть усвоено очень рано и должно пронизывать
все преподавание алгебры и геометрии»
Понятие функциональной зависимости является одним из ведущих в
математической науке, поэтому сформированность этого понятия у учащихся
представляет важную задачу в целенаправленной деятельности учителя по развитию
математического мышления и творческой активности детей. Развитие
функционального мышления предполагает прежде всего развитие способности к
обнаружению новых связей, овладению общими учебными приемами и умениями.
Чтобы подготовить учеников к сознательному усвоению идеи функциональной
зависимости, понятий функции и уравнения в VII и более старших классах школы,
необходимо заранее и постепенно подготовить их к знакомству с этими понятиями.
Пропедевтика функциональной зависимости способствует формированию мыслительных
операций и воспитанию интеллектуальных качеств личности. Направления подобной
работы выражаются в характере задач, предлагаемых учащимся. В плане подготовки
должны быть использованы всевозможные упражнения, которые не ведут
непосредственно к каким-либо обобщениям, но доступны ученикам младших классов и
могут служить для накопления ими опыта. Этот опыт будет создавать у них необходимые
представления, ведущие к образованию соответствующих понятий на конкретной
числовой и графической основе. Далекие от обобщений и специальной терминологии,
эти упражнения должны помочь учащимся выяснить, что рассматриваемое ими одно и
то же выражение может приобретать различные значения в зависимости от числовых
значений входящих в него букв. Эти упражнения должны помочь учащимся понять
различные способы выражения функциональных зависимостей.
Материал начального математического курса содержит достаточное количество
примеров, на которых можно разъяснить зависимость одной величины от другой. К
ним, в частности, относятся: задачи на составление и решение уравнений,
оптимизационные и комбинаторные задачи, задачи с величинами, находящимися в
прямой и обратной зависимости, задачи с использованием таблиц, числовой оси и
координатной плоскости.
В школе, как и в математике вообще, основное внимание уделяется числовым
функциям. Причиной этого является тесная связь математики с естественными
науками, в частности с физикой, для которых аппарат функций служит средством
количественного описания свойств и явлений, их взаимосвязей.
Понятие функции учащимися воспринимается с трудом; очевидно, сказывается
привычка как в математике, так и в начале алгебры рассматривать лишь постоянные
величины (в условии данной задачи).
Функциональная пропедевтика помогает облегчить переход к изучению
переменных величин. Опосредованная пропедевтика предполагает постепенную
функциональную подготовку, не требующую ни специальной терминологии, ни
символики; достаточно последовательно проводить идею изменяемости окружающего
мира; давать ученикам упражнения, которые формируют понятие переменной
величины, взаимосвязь между величинами, используя для этой цели материал
школьных учебников. Объективные возможности для пропедевтики имеются, учитель
должен их видеть и использовать в обучении школьников.
3.2 Функциональная пропедевтика на уроках математики в V классе
В V классе можно указать ряд упражнений, в которых учащиеся имеют дело в
скрытой форме с переменными величинами. К ним относятся упражнения на изменение
суммы, разности, произведения и частного дроби.
Например, вопрос, как изменится произведение, если множитель увеличить в
2 раза, связан с изменением произведения в зависимости от изменения множителя.
Чтобы приучать к понятию переменной величины, можно вопрос задать иначе: как
изменится произведение, если один множитель увеличить в 2 раза? В 3 раза? В 4
раза? В 5 раз? Такие упражнения дадут пятиклассникам некоторое представление о
переменных величинах. Полезно при записи решения подобных упражнений
использовать таблицы. Они наглядны и в то же время это табличная запись
функциональной зависимости.
Пример: Как изменится сумма двух чисел, Если второе слагаемое увеличить
на 1, 2, 3, 7, 12, 20, 30, 50, 92?
После устного ответа учеников им можно показать процесс изменения суммы,
когда один из компонентов остается неизменным, а другой меняется, c помощью таблицы. Таблице можно
придать следующий вид:
|
Первое слагаемое
|
3
|
3
|
3
|
3
|
3
|
3
|
|
Изменение второго слагаемого
|
+1
|
+2
|
+3
|
+7
|
+12
|
+20
|
|
Изменение суммы
|
+1
|
+2
|
+3
|
+7
|
+12
|
+20
|
Рассматривая эту таблицу, легко установить зависимость результата от
величины второго слагаемого и характер изменения суммы. Так, можно предложить
ученикам сравнить изменение второго слагаемого и соответствующее изменение
суммы. Второе слагаемое увеличено на 1, 2, 3, 7…, сумма, соответственно
увеличилась на 1, 2, 3, 7…
Затем полезно дать такие упражнения, в которых изменяются оба слагаемых.
Аналогичные упражнения дают и на изменение разности, произведения,
частного (дроби). Термины учащимся не сообщают, но обращают их внимание на то,
что в задаче величины принимают различные значения.
В 5 классе при повторении и изучении геометрического материала появляется
возможность углубить понятие о переменной величине. Так, например, периметр
прямоугольника при выбранной длине основания будет меняться в зависимости от
высоты прямоугольника. Длина периметра при длине основания, равной 4 единицам,
и меняющейся высоте будет выражаться: Р=8+2х.
Такая же работа может быть проведена при нахождении площади
прямоугольника, у которого длина основания 4, а высота меняется.
При решении текстовых задач в 5 классе ученики используют различные
функциональные зависимости.
Наиболее часто встречаются зависимости:
путь, скорость и время;
стоимость, цена и вес;
стороны и периметр квадрата, прямоугольника;
стороны и площадь прямоугольника;
работа, оплата и время работы и т. д.
Знание учениками этих зависимостей - залог успешного решения задач на
составление уравнений и последующего изучения функциональной зависимости в
алгебре.
Задачи по математике можно задать так, что некоторые величины предстанут
как переменные.
Задача 1.
Велосипедист проезжает за час 12 км. Сколько проедет он за 1 час; 1,5
часа; 2 часа; 2,5 часа; 3 часа?
При решении учащиеся устанавливают зависимость между величинами: путь
равен скорости, умноженной на время движения.
|
Скорость (км/ч)
|
12
|
12
|
12
|
12
|
12
|
|
Время (ч)
|
1
|
1,5
|
2
|
2,5
|
3
|
|
Расстояние (км)
|
12
|
18
|
24
|
30
|
36
|
В отношении функциональной пропедевтики здесь существенно следующее:
) установлена зависимость между величинами;
) сделана табличная запись зависимости;
) в таблице время и путь выступают как переменные величины, а скорость -
постоянная.
Выполнение таких упражнений и повторение время от времени различных
функциональных зависимостей постепенно приучают учащихся к тому, что есть
величины, которые могут менять своё значение, причём в зависимости от изменения
одной величины (например, времени) другая величина (путь) принимает
определённое значение.
Кроме того, учеников надо готовить к графикам.
Уже в 5 классе можно предложить изображать нуль, целые и дробные числа на
числовом луче.
Если это будет введено, то можно для некоторых задач дать арифметическое
решение с помощью очень простых номограмм (этот термин ученикам не сообщают).
Задача 2
Цена кукурузной крупы 20 коп. за кг. Сколько стоит 1 кг; 1,5 кг; 2 кг;
2,5 кг; 3 кг; 4 кг; 5 кг; 6 кг; 7 кг; 8 кг; 9 кг; 10 кг?
Составить таблицу и показать зависимость на графике.
Решение будет в виде таблицы.
|
Цена (к/кг)
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
20
|
|
Вес (кг)
|
1
|
1,5
|
2
|
2,5
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Стоимость (к)
|
20
|
30
|
40
|
50
|
60
|
80
|
100
|
120
|
140
|
160
|
180
|
200
|
Отложим на числовом луче полученные значения веса сверху и стоимости
снизу.
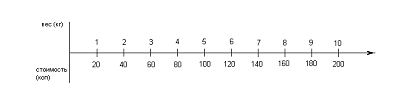
Затем ученикам показывают, как, пользуясь полученным графиком, можно
сразу находить по данному весу стоимость и наоборот.
Такие графики-номограммы можно приготовить для различных задач по схеме
путь = скорость × время, скорость = путь / время и т. д.
Можно предложить задачи и на обратную пропорциональность. Например, число
м = стоимость покупки / цена м.
Такие упражнения, давая понятие переменной величины и функциональной
зависимости, однако не готовят учеников к графикам, выполненным на координатной
плоскости. Для такой подготовки полезно вычерчивать столбчатые диаграммы.
Учащиеся должны их выполнять на миллиметровке или на бумаге в клетку.
Тематика для таких диаграмм в 5 классе может быть различной:
сопоставление данных семилетнего плана, сравнение урожайности, высоты гор,
длины рек, численности населения, тоннаж торговых судов, потолок различных
самолётов и т. д.
Для первых упражнений лучше брать наиболее простые условия.
Пример: В семье, состоящей из четырёх человек, рост отца 170 см, рост
матери 162 см, рост сына 120 см и рост дочери 140 см. изобразить их рост на
диаграмме.
Выбираем масштаб: в 1 клетке 20см.
Тогда росту отца соответствует 170:20=8,5 (кл);
Росту матери - 162:20=8,1 (кл);
Росту сына - 120:20=6 (кл);
Росту дочери - 140:20=7 (кл).
На диаграмме наглядно изображено, кто выше и на сколько.
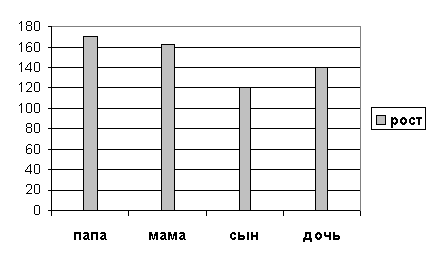
Диаграммы
в виде вертикальных столбиков или отрезков прямой особенно следует
рекомендовать, так как от них проще всего перейти к координатной системе,
столбик или отрезок - ордината. Ученики к ним и потом, когда на чертеже будет
отмечен только конец столбика - ординаты, они будут знать, что отрезок
подразумевается.
В
следующих диаграммах можно сопоставить высоту горных вершин, а затем рост
производства основных видов промышленной продукции по семилетнему плану по
сравнению с предыдущими годами.
Подобные
диаграммы можно делать как в 5, так и в 6 классе. Материал для них можно взять
из географических атласов, сводок о выполнении годового плана и т.д.
3.3 Функциональная пропедевтика на уроках математики в VI классе
В 6 классе функциональная пропедевтика расширяется. По математике,
рассматривая прямую и обратную пропорциональность, дают табличные записи этой
функциональной зависимости, формулы у=кх, у=к/х;на уроках математики вводят
буквенные обозначения, где под буквой подразумевается любое допустимое
значение, то есть буква обозначает переменную величину.
Полезно больше делать упражнений, в которых надо находить значение
алгебраического выражения не при одном значении буквы, входящей в выражение, а
брать несколько таких значений, чтобы показать зависимость значения выражения
от значений входящих в него букв.
Пример 1:
Вес детали 24 кг, площадь её основания s см2. её поставили на
горизонтальную опорную плоскость. Выразить давление детали на 1 см2
опоры. Составить таблицу значений давления для s=1, 2, 3, 4, 5, 6, 7, 8.
Решение
Давление на 1 см2 равно 24/ s (кг/ см2).
|
s
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
24/ s
|
24
|
12
|
8
|
6
|
4,8
|
4
|
3,43
|
3
|
В заключение можно сделать столбчатую диаграмму.
Пример 2
Дано
выражение  .
.
Найти
его значение при а=0, 1, 2, 3, 4, 5, 6.
Результат
записать в виде таблицы и сделать столбчатую диаграмму.
Таблица:
Диаграмма:
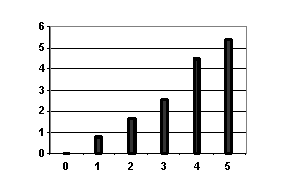
Учитель
подчёркивает, что значение выражения  зависит
от значений а.
зависит
от значений а.
Подобные
упражнения целесообразно проводить в 6 классе и даже включать в них небольшой
элемент исследования.
Пример 3:
Выполнить действие:
-8а : (-4а) и найти значение частного при а=0; -5; -1;
-0,1; 3,5.
: (-4а) и найти значение частного при а=0; -5; -1;
-0,1; 3,5.
Что
можно сказать о знаке частного?
Решение:
а : (-4а)=а
: (-4а)=а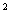 ,
,
|
а
|
-5
|
-3
|
-1
|
0
|
1
|
3
|
5
|
|
-8а : (-4а)2591Не имеет смысла1925 : (-4а)2591Не имеет смысла1925
|
|
|
|
|
|
|
|
-8а : (-4а)= а
: (-4а)= а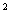 , при а≠0.
, при а≠0.
Вывод:
Частное может принимать только положительные значения (не может принимать
отрицательных значений и быть нулём).
При
решении примеров на тождественные преобразования учитель может ставить
аналогичные вопросы.
Полезно
составлять формулы. Хороший материал для этого имеется в курсе 6 класса. Можно
предложить такие упражнения.
1. Острые углы прямоугольного треугольника равны α
и β.
Найти зависимость между
ними. (α
+ β = 90°).
2. Периметр равнобедренного треугольника равен Р, боковая сторона
а, основание в. Составить формулу, по которой находят: а) Р по данным а и в;
б) в по данным а и Р;
в) а по данным Р и в.
3. Угол при вершине равнобедренного треугольника равен β,
а при основании α.
Составить формулу по
которой находят:
а) β по данному α ;
б) α по данному β.
. пусть в треугольнике сторона равна а, соответствующая ей средняя линия
равна d. Составить формулу по которой находят:
а) d, зная а;
б) а, зная d.
Составить таблицу значений d, если а=1; 1,8; 2; 2,5; 3; 4; 5; 6; 7; 8, и
построить график зависимости d от a.
Последний пример предназначен для учеников VII класса.
Можно предложить упражнения, в которых ставится вопрос о значениях
независимой переменной, при которых две функции равны, а также упражнения,
содержащие вопрос о корнях функций.
Пример 1:
При каких значениях x следующие выражения равны между собой:
1) х-3 и 5;
2) 2х-3 и 8;
3)  и 4;
и 4;
) 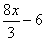 и 10;
и 10;
)  и -5.
и -5.
Пример 2:
При каких значениях х следующие выражения равны нулю:
1) 2х;
2) 3х-4;
3) 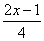 ;
;
)  ;
;
) 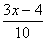 .
.
После того как ученики ознакомятся с построением элементарных графиков,
им можно показать их построение для случая, когда берется вся координатная
плоскость.
Здесь можно дать интересные упражнения связанные со сложением
рациональных чисел.
Пример 3:
Наблюдение за температурой проводилось раз в день (в 12 ч) на протяжении
9 дней. Изменение температуры показано на графике.

Записать, насколько менялась температура ежедневно, сложить полученные
числа и сравнить полученную сумму с изменением температуры за 9 дней по
чертежу.
Решение
По графику за эти дни температура поднялась с -2º до +5º, то есть поднялась на 7º, изменение равно +7º.
Сумма изменений по дням: (+4) + (-1) + 0 + (+2) + 0 + (+1) + (-2) +
+ (+3) = 7 (град.)
Такие упражнения даются на протяжении всего курса алгебры в VI-VIII
классах. Цель их, не вводя новых терминов, формировать понятие переменной
величины и функциональной зависимости с помощью упражнений.
Определяя
допустимые значения букв, лучше говорить не о множестве их, а добиваться от
учащихся понимания того, что в некоторых частных случаях выражение не имеет
смысла. Например, ученик после действий над алгебраическими дробями получил
ответ 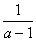 ; целесообразно поставить вопрос: найти значение
полученного результата при а = -2; -1; 0; 1; 2; 3; 5; 6. Получится таблица:
; целесообразно поставить вопрос: найти значение
полученного результата при а = -2; -1; 0; 1; 2; 3; 5; 6. Получится таблица:
|
а
|
-2
|
-1
|
0
|
1
|
2
|
3
|
5,6
|
|
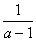 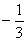 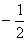 -1Не имеет смысла1 -1Не имеет смысла1 
|
|
|
|
|
|
|
|
В функциональной пропедевтике учителю надо тактично соблюдать меру и
помнить, что в первую очередь надо знакомить учеников с основным материалом, а
представление о переменных и функциональной зависимости формировать попутно, не
давая терминов.
Глава 4. Анализ учебников по математике авторов Н.Я.
Виленкина и Л.Г. Петерсон для 5 и 6 классов
В настоящее время проблемам преподавания математики в школе стали
уделять больше внимания. Это связано с научно-техническим прогрессом и
развитием наукоемких производств. Технические науки, среди которых, в последнее
время, быстро развиваются и имеют огромное практическое значение, такие как
информационные технологии, электроника и т.д., немыслимы без математического
аппарата.
Основа для математической грамотности закладывается именно в школе,
поэтому изучению вопросов, связанных с этим процессом, уделяется пристальное
внимание. Математика является одним из опорных предметов школы. Она
обеспечивает изучение других дисциплин. Требует от учащихся волевых и
умственных усилий, развитого воображения, концентрации внимания, математика
развивает личность учащегося. Кроме того, изучение математики существенно
способствует развитию логического мышления и расширяет кругозор школьников.
Успешность преподавания математики, как и остальных предметов школьной
программы, определяют многие факторы, среди которых, как основной, выделяют
выбор методики преподавания. Именно от правильного выбора методов и приемов
преподавания каждой темы курса и их удачного сочетания, зависит уровень
понимания, в конечном счете, учащимися материала.
В ходе изучения курса учащиеся развивают навыки вычислений с натуральными
числами, овладевают навыками действий с обыкновенными и десятичными дробями,
положительными и отрицательными числами, получают начальные представления об
использовании букв для записи выражений и свойств, учатся составлять по условию
текстовой задачи несложные линейные уравнения и решать их, продолжают знакомство
с геометрическими понятиями, приобретают навыки построения геометрических фигур
и измерения геометрических величин.
Современная алгебра исходит из определения
рассматриваемого понятия, предложенного в 19 веке российским ученым Н.И.
Лобачевским, выражающего зависимость между переменными величинами: функцией от
х называется число, которое дается для каждого х и вместе с х постепенно
изменяется; функция - это зависимая переменная. Через понятие функции в
математике моделируются реальные диалектические процессы, изменения,
взаимозависимости и взаимообусловленности. Идея функциональной зависимости
находит свое отражение не только в математике, но и в ряде других наук -
физике, химии, биологии, медицине, истории, кибернетике. Велика роль функции
как мощного аппарата в познании процессов, происходящих в реальном мире. Знание
функциональных зависимостей помогает найти ответы на разнообразные вопросы - от
расшифровки памятников древности до управления сложнейшими производственными
процессами. Наблюдая веками явления природы, человек замечал соответствие между
ними. Систематизируя и обобщая устойчивые взаимосвязи в природе, он познал
закономерности и учился применять их для объяснения разнообразных явлений
природы. Математическими моделями таких закономерностей и являются функции.
Таким образом, в начальном курсе математики
значительная роль должна отводиться функциональной пропедевтике, которая
предусматривает подготовку учащихся к изучению систематических курсов алгебры и
геометрии, а также воспитывает у них диалектический характер мышления,
понимание причинных связей между явлениями окружающей действительности.
Предмет математики V - VI классов объединяет много
разноплановых понятий (числа, сравнения чисел, действия над числами и законы
этих действий, переменная, неравенство, пропорция, процент, геометрические
фигуры и их свойства и др.). Объединяющими средствами при построении учебного
предмета являются единые методические подходы в изложении родственных понятий.
Таким образом, использование единых методических подходов, позволяет добиться
сознательного понимания сущности математических действий и понятий учащимися.
Приведем некоторые их этих методических приемов:
. Пропедевтика функции, в частности однозначное
соответствие и алгебраические начала, позволяет при введении новых чисел, их
сравнении, иллюстрации действий систематически использовать луч и координатную
прямую.
. Систематическое изучение законов арифметических
действий позволяет использовать единые методические приемы в обосновании
алгоритмов, решении уравнений и тождественных преобразований выражений.
. Благодаря введению понятия переменной и однозначного
соответствия стало возможным более широкое использование таблиц, графиков,
формул, схем.
. Введение выражений с переменной, уравнений и
неравенств позволило изменить виды задач с дидактическими и познавательными
функциями при изучении числовых множеств и уже в V - VI классах показать
практическую применимость новых числе и действий над ними в самом предмете
математики.
В этой связи обозначим основные направления
пропедевтической работы на начальной ступени обучения предмету по программам
Л.Г. Петерсон и Н.Я. Виленкина:
Понятие о множествах, о соответствии элементов двух
множеств и функциях. Зависимость результатов арифметических действий от
изменения компонентов.
Числовые выражения с 3-4 арифметическими операциями
(со скобками и без них), вычисление их значений.
Буквенные выражения. Переменные величины. Вычисление
их значений при подстановке численных значений переменных.
Представление о числовых последовательностях.
Изменение численных значений величин при использовании
различных единиц измерения.
Математические исследования.
Табличный, словесный, аналитический, графический
способы задания функции.
Линейная зависимость.
Система координат, первая и вторая координата,
упорядоченная пара.
Решение простейших комбинаторных задач: составление и
подсчет числа возможных перестановок, подмножеств элементов конечного
множества.
Представление о возможности неограниченного увеличения
натурального числа или уменьшение его доли.
Использование систематического перебора натуральных
значений одной и двух переменных при решении сюжетных задач.
Заполнение таблиц с арифметическими вычислениями,
данными из условий прикладных задач. Выбор данных из таблицы по условию.
Зависимость между пропорциональными величинами;
прикладное исследование их графиков.
Проиллюстрируем сказанное конкретными примерами из
учебников по математике:
Содержание начального курса математики позволяет
сформировать у учащихся представление об одной из важнейших идей математики -
идее соответствия. При выполнении заданий на нахождение значений выражений,
заполнение таблиц ученики устанавливают, что каждой паре чисел соответствует не
более одного числа, полученного в результате. Однако для осознания этого
содержание таблиц необходимо анализировать.
. Составь все возможные примеры на сложение двух
однозначных чисел с ответом 12. (Петерсон)
При выполнении этого задания учащиеся устанавливают
взаимосвязь между двумя множествами значений слагаемых. Установленное
соответствие - функция, так как каждому значению первого слагаемого
соответствует единственное значение второго слагаемого при постоянной сумме.
. В вазе 10 яблок. Сколько яблок останется, если
возьмут 2 яблока? 3 яблока? 5 яблок? Запиши решение в таблице. От чего зависит
результат? На сколько единиц он изменяется? Почему? (Петерсон)
В данной задаче фактически представлена функция у = 10
- х, где переменная х принимает значения 2, 3, 5. В результате выполнения
данного задания учащиеся должны сделать вывод: чем больше вычитаемое, тем
меньше значение разности.
. Как изменится однозначное число, если к немее
приписать такое же число? Два таких числа? (Виленкин)
Идея функционального соответствия присутствует и в
упражнениях вида:
. Соедини стрелкой математические выражения и
соответствующие численные значения (Петерсон) :
+ 6 18 + 9 21 - 4 38
- 19
19 17 21 35 40 15
В V - VI классах частично-поисковым методом можно изучить следующие
понятия: переменная, выражения с переменной, равенство, верное и неверное
равенство, уравнение и неравенство, сравнение чисел, числовая прямая, действия
в каждом из числовых множеств и т.п.
При использовании этого метода изучения нового материала обычно
соблюдается следующая последовательность действий учителя и учащихся:
. Решаются дидактические упражнения с целью организации наблюдений и
простейшего анализа для выявления какой-либо закономерности. Поэтому важно,
чтобы упражнения полно раскрывали структуру понятия.
. В процессе решения дидактических упражнений учитель ставит
дополнительные вопросы и задания к ним для выяснения всех доступных учащимся
сторон изучаемого понятия, раскрытия зависимостей и противоречий.
. На основе наблюдений и анализа решенных заданий, выяснения свойств и
зависимостей изучаемого понятия учащиеся под руководством учителя делают вывод
о формируемом понятии, устанавливают связь изучаемого материала с ранее
изученным и т.п.
. И, наконец, решают упражнения на применение полученных знаний о
понятии, т.е. перенос знаний на новую ситуацию.
Рассмотрим использование метода, на примере введения понятия о
координатах точек на прямой по учебнику Виленкина Н.Я. для 5 класса.
В учебнике разбираются следующие дидактические задания, для формирования
понятия:
. Белка вылезла из дупла и бегает по стволу дерева вверх и вниз (см.
рисунок 1). Покажите, где будет находится белка, если она удалится от
дупла на 3 м. Сколько ответов можно дать на этот вопрос? Покажите на
рисунке, где окажется белка, если она будет находится: а) выше дупла на
м; б) ниже дупла на 3 м;
в) ниже дупла на 1,5 м; г) выше дупла на 2,5 м.
Введение буквенной символики позволяет познакомить учащихся с важнейшими
понятиями современной математики - переменная, уравнение, неравенство, что
способствует развитию функционального мышления, поскольку с ними тесно связана
идея функциональной зависимости. При работе с переменной школьники осознают,
что буквы, входящие в выражение, могут принимать различные числовые значения, а
само буквенное выражение является обобщенной записью числовых выражений. Одни
из примеров системного использования буквенной символики являются задачи,
представленные в блиц-турнирах. Отсутствие конкретных чисел заставляет учеников
искать путь решения задачи, опираясь на существенные связи между данными и
искомыми. Эта модель задачи - знаковая, она более абстрактна, чем числовое
выражение. При этом ученик не может вычислить промежуточные результаты, а
должен представлять всю цепочку связей между величинами и выстраивать
соответствующую последовательность действий. Исследование решения задач с
буквенными данными предполагает рассмотрение различных соотношений между
значениями букв, а так же выявление возможности или невозможности принятия
буквой конкретных числовых значений, установление влияния числовых значений
переменных на количество способов решения задачи. Огромное пропедевтическое
значение имеет опыт общения учащихся с упражнениями на установление
закономерностей в числовых последовательностях и их продолжение:
. 1, 2, 3, 4… (у = х + 1)
, 3, 5, 7… (у = 2 · х + 1) (Петерсон)
. продолжите ряд чисел:
, 7, 13, 19, …(Виленкин)
Понятие величины, наряду с понятием числа, является основным понятием
начального курса математики. Материал данного раздела является богатейшим
источником для осуществления опосредованной функциональной пропедевтики.
Во-первых, это зависимость (обратнопропорциональная) между выбранной единицей
величины (меркой) и ее численным значением (мерой) - чем больше мерка, тем
число, полученное в результате измерения величины данной меркой, меньше.
Поэтому важно, чтобы при работе с каждой величиной (длиной, массой, площадью,
объемом и пр.) учащиеся приобретали опыт измерения величин разными мерками с
целью осознанного выбора сначала удобной, а затем и единой мерки.
Во-вторых, при изучении величин, характеризующих процессы движения,
работы, купли-продажи формируются представления о зависимости между скоростью,
временем и расстоянием, ценой, количеством и стоимостью в процессе решения
текстовых задач следующих видов - на приведение к единице (нахождение
четвертого пропорционального), нахождение неизвестного по двум разностям,
пропорциональное деление.
Особую сложность для учащихся представляет осознание взаимосвязи между
этими величинами, поскольку понятие «пропорциональная зависимость» не является
предметом специального изучения и усвоения. В программе Л.Г. Петерсон
методически эта проблема решается за счет использования следующих приемов:
- Решение задач с недостающими данными («открытым» условием):
7. Васе от дома до школы 540 м, а Паше - 480 м. Кто ближе живет? Кто быстрее
дойдет?
. Саша купил на 30 рублей тетради и на 45 рублей карандаши. На покупку
каких предметов он истратил денег больше? Каких предметов он купил больше?
Анализируя тексты этих задач, учащиеся обнаруживают, что в них не хватает
данных и что ответы на вопросы зависят от цены и скорости.
Фиксация условия задач не только в таблице (как это
предложено в классической методике), но и в виде схемы. Это позволяет «визуализировать»
зависимости, рассматриваемые в задаче. Так, если одно и тоже расстояние в 12 км
движущиеся объекты проходят за разное время (2 ч, 3 ч, 4 ч, 6 ч), то с помощью
схемы наглядно интерпретируется обратная зависимость - чем больше частей
(время), тем меньше каждая часть (скорость).
- Изменение одного из данных задачи и сравнение результатов
решения задач.
9. В школьную столовую привезли 48 кг яблок. Сколько ящиков могли
привезти, если во всех ящиках яблок было поровну?
Учащиеся дополняют условие задачи и фиксируют зависимость между
величинами с помощью различных средств структурирования теоретических знаний -
в таблице, схеме и словесно.
Здесь же полезно обратить внимание на кратное отношение рассматриваемых
величин - во сколько раз больше одна из величин, во столько же раз больше
(меньше) другая при постоянной третьей.
В начальной школе учащиеся в неявном виде знакомятся с
табличным, аналитическим, словесным, графическим способами задания функций.
Так, например, зависимость между скоростью, временем и расстоянием можно
выразить:
а) словесно: «чтобы найти расстояние, нужно скорость умножить на время»;
б) аналитически: s= u ·t;
в) таблично: u =5
км/ч
|
t
|
1
|
2
|
3
|
t
|
|
s
|
5 · 1
|
5 · 2
|
5 · 3
|
5 ∙ t
|
г) графически (с помощью координатного луча или угла).
Графический способ задания зависимости между u, t, s позволяет
сформировать представление о скорости как изменении местоположения движущего
объекта в единицу времени (наряду с общепринятым - как расстояния, пройденного
в единицу времени) А сравнение графиков движения двух тел (движущихся
независимо друг от друга) уточняет представление о скорости как величине,
характеризующей быстроту движения.
Составные числовые выражения (со скобками и без них),
вычисление их значений по правилам порядка выполнения действий позволяет
учащимся осознать, что от порядка выполнения действий зависит результат.
Расставьте скобки так, чтобы получились верные
равенства.
+ 30 : 5=10 20 + 30 : 5 = 26
В курсе Л.Г. Петерсон учащиеся в неявном виде
знакомятся с линейной зависимостью, как частным случаем функции. Эту функцию
можно задать формулой вида у = kх + b, где х - независимая переменная, k и b - числа. Ее областью определения являются множество всех
действительных чисел.
Пройдя 350 километров, поезд стал идти в течение t часов со скоростью 60 км/ч. Сколько
всего километров прошел поезд? (350 + 60 · t)
Выполняя задания с именованными числами, учащиеся
осознают зависимость численного значения величин от использования различных
единиц измерения.
Один и тот же отрезок измерили сначала в сантиметрах,
затем в дециметрах. В первом случае получили число на 135 больше, чем во
втором. Какова длина отрезка в сантиметрах? (Зависимость у = 10 · х)
В процессе изучения начального курса математики у
учащихся формируется понятие натурального ряда чисел, отрезка натурального
ряда, усваиваются свойства натурального ряда чисел - бесконечность, упорядоченность
и др., формируется представление о возможности неограниченного увеличения
натурального числа или уменьшение его доли.
В курсе математики 3-4 классов значительное внимание
уделено обучению учащихся использованию формул, их самостоятельному выводу.
Здесь важно научить учащихся представлять одну и ту же информацию в различной
форме - графически и аналитически, предоставив школьникам право выбора формы в
соответствии с их познавательными стилями.
Значительный интерес у учащихся вызывают задания, связанные
с анализом таблиц значений переменных, «открытие» зависимостей между ними и
запись в виде формулы.
|
а
|
1
|
2
|
3
|
4
|
5
|
6
|
а
|
|
b
|
5
|
9
|
13
|
17
|
21
|
25
|
а · 4 + 1
|
При анализе чисел, представленных в таблице, учащиеся
легко подмечают, что числа первой строки увеличиваются на один, числа второй
строки увеличиваются на четыре. Задача учителя - обратить внимание на
взаимосвязь значений переменных а и b. В целях усиления прикладной направленности математического образования
следует «оживить» данную ситуацию, перевести ее в сюжетный статус.
Чтобы сформировать у учащихся способность к выводу
формул, нужно научить их записывать различные утверждения на математическом
языке (в виде равенств):
ручка в три раза дороже карандаша (р = к + 3);
число а при делении на 5 дает в остатке 2 (а = 5 · b + 2);
длина прямоугольника на 12 см больше ширины (а = b + 12).
Обязательным условием является обсуждение возможных
вариантов значений данных величин с заполнением соответствующих таблиц.
Особое место в курсе Л.Г. Петерсон занимают задания,
связанные с математическими исследованиями:
Представь число 16 в виде произведения двух множителей
разными способами. Для каждого способа найди сумму множителей. В каком случае
получилась меньшая сумма? Проделай это же с числами 36 и 48. Каково предположение?
При выполнении подобных заданий (на исследование
зависимости между количеством углов многоугольника и суммарным значением
градусных мер углов, между значением периметра различных по форме фигур с
одинаковой площадью и пр.) учащиеся совершенствуют навыки работы с таблицей,
так как решение удобно фиксировать в таблице. Кроме этого табличный способ
фиксации решения используется при решении нестандартных математических задач
методом упорядоченного перебора или рационального подбора.
В классе 13 детей. У мальчиков столько зубов, сколько
у девочек пальцев на руках и ногах. Сколько в классе мальчиков и сколько
девочек? (У каждого мальчика ровно 32 зуба).
|
Мальчики
|
Девочки
|
Проверка
|
|
8
|
5
|
32 · 8 # 20 · 5
|
|
7
|
6
|
32 · 7 # 20 · 6
|
|
5
|
8
|
32 · 5 = 20· 8
|
Обучение математике по программе Л.Г. Петерсон
обеспечивает усвоение учащимися взаимосвязи между результатами и компонентами
арифметических действий, формируется представление о «скорости» изменения
результата арифметических действий в зависимости от изменения компонентов:
упражнения на состав числа;
частные приемы вычислений (36 + 19 = 35 + 20; 36 - 19
= 37 - 20; 12 · 5 = 12 · 10 : 2);
оценка суммы, разности, произведения, частного.
При выполнении подобных заданий важно представлять
информацию многосенсорно.
Как изменится сумма, если одно слагаемое увеличить на
10, а второе уменьшить на 5?
Как изменится площадь прямоугольника (или произведение
двух чисел), если одну из сторон (одно из чисел) увеличить на 3?
Наши исследования показывают, что значительная часть
учащихся выполняют подобные задания методом подстановки конкретных числовых
значений. Методически грамотным в данной ситуации будет графически и
аналитически интерпретировать условие.
(а + 3) · b = а · b + 3 · b
Понятие функции в старших классах связано с системой
координат. В курсе Л.Г. Петерсон содержится материал для пропедевтической
работы в этом направлении:
числовой отрезок, числовой луч, координатный луч;
таблица Пифагора, координаты на плоскости
(координатный угол);
графики движения;
круговые, столбчатые и линейные диаграммы, наглядно
представляющие зависимость между дискретными величинами.
Итак, изучение арифметических операций, увеличения и
уменьшения числа на несколько единиц или в несколько раз, зависимости между
компонентами и результатами арифметических действий, решение задач на
нахождение четвертого пропорционального, на связь между скоростью, временем и
расстоянием; ценой, количеством и стоимостью; массой отдельного предмета, их
количеством и общей массой; производительностью труда, временем и работой; и т.
д., с одной стороны, лежат в основе формирования понятия функции, а с другой -
изучаются на основе функциональных понятий. Следует отметить, что достаточно
большое пропедевтическое значение имеет графическое моделирование: графическая
интерпретация условия задачи, рисунок, чертеж и другое. Информация,
представленная в графической форме, легче для восприятия, емкая и достаточно
условная, призвана опредмечивать абстрактные понятия, нести информацию лишь о
существенных признаках объекта, формировать графические навыки учащихся.
Обобщая, отметим, что основные цели изучения учебного содержания
функциональной линии курсов Л.Г. Петерсон и Н.Я. Виленкина:
) развитие функционально-аналитического мышления школьников,
характеризующегося способностью рассматривать объекты, в том числе и
математические, во взаимосвязи и взаимозависимости;
2) формирование у учащихся способности к выражению
зависимости между величинами разными способами (таблично, аналитически,
графически).
Кроме этого, результатом пропедевтики функциональной
зависимости должна стать высокая умственная активность младших школьников,
развитие интеллектуальных, общепредметных и специфических математических умений
и навыков. Все это создает прочную основу не только для решения методических
проблем начальной математики - формирование вычислительных навыков, умения
решать текстовые задачи и др., но и для реализации развивающих возможностей
математического содержания и, что не менее важно, для успешного изучения
функций в средней школе.
Заключение
Итак, чтобы подготовить учеников к сознательному
усвоению идеи функциональной зависимости, понятий функции и уравнения в VII и
более старших классах школы, необходимо заранее и постепенно подготовить их к
знакомству с этими понятиями.
В плане подготовки должны быть использованы
всевозможные упражнения, которые не ведут непосредственно к каким-либо
обобщениям, но доступны ученикам младших классов и могут служить для накопления
ими опыта. Этот опыт будет создавать у них необходимые представления, ведущие к
образованию соответствующих понятий на конкретной числовой и графической
основе. Далекие от обобщений и специальной терминологии, эти упражнения должны
помочь учащимся выяснить, что рассматриваемое ими одно и то же выражение может
приобретать различные значения в зависимости от числовых значений входящих в
него букв. Эти упражнения должны помочь учащимся понять различные способы
выражения функциональных зависимостей.