Использование прогнозирования в эконометрике

Практическое использование прогнозирования в эконометрике

СОДЕРЖАНИЕ

ВВЕДЕНИЕ......................................................................................................... 3

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ........................................................................... 6

1.1. Сущность и назначение прогнозирования на основе временных рядов... 6

1.2. Методика применения авторегрессивных моделей.................................. 14

1.3. Методика применения моделей скользящей средней в эконометрике.... 22

2. ПРАКТИЧЕСКАЯ ЧАСТЬ........................................................................... 26

ЗАКЛЮЧЕНИЕ................................................................................................. 36

СПИСОК ЛИТЕРАТУРЫ................................................................................ 37

ПРИЛОЖЕНИЯ................................................................................................ 38

ВВЕДЕНИЕ

Термин эконометрия (эконометрика) был введен в научную литературу в 1930 году норвежским статистиком Рагнаром Фришем[1] для обозначения нового направления научных исследований, возникшего из необходимости научно-обоснованного подтверждения и доказательства концепций и выводов экономической теории результатами количественного анализа рассматриваемых процессов. В этой связи можно сказать, что основная задача эконометрики состоит в построении моделей специфического типа (эконометрических моделей), описывающих взаимообусловленное развитие социально-экономических процессов, на основе информации, отражающей распределение их уровней во времени или (и) в пространстве однородных объектов. Эти модели используются в анализе и прогнозировании общих закономерностей и конкретных количественных характеристик рассматриваемых процессов, определении управляющих воздействий. Вследствие этого в самом широком толковании эконометрию можно рассматривать как объединение ряда дисциплин – экономической теории (включая микро- и макроэкономику, социальную сферу), социально-экономической статистики и теории измерения общественных процессов, математической статистики и методов экономико-математического моделирования.

Каждая из перечисленных дисциплин играет свою роль в эконометрическом исследовании. Экономическая теория занимается вопросами разработки концепций относительно законов развития исследуемых процессов с учетом их взаимосвязей; социально-экономическая статистика и теория измерений – выражением количественных и качественных состояний этих процессов (как правило, в последовательные периоды (моменты) времени) в виде набора логически непротиворечивых и содержательных показателей; методы экономико-математического моделирования – разработкой моделей взаимосвязей между рассматриваемыми процессами, адекватно отражающими экономические концепции в рамках выбранной системы показателей; математическая статистика – собственно построением самих моделей (т. е. оценкой их параметров), проверками гипотез относительно их адекватности тенденциям процессов, значимости взаимосвязей между ними, оценками неопределенности в полученных результатах, вызванной систематическими и случайными ошибками и т. п.

При этом обычно предполагается, что систематические ошибки в результатах возникают вследствие использования неадекватной тенденциям исследуемых процессов концепции относительно их взаимосвязей, систематических ошибок измерений их уровней, неправильно выбранной спецификации модели и ряда других причин объективного и субъективного характера.

Причинами существования случайной ошибки модели, как правило, являются случайные ошибки измерения процессов, невозможность учета в модели случайных воздействий множества незначимых с точки зрения экономической теории факторов и другие подобные причины.[2]

Таким, образом, учитывая все вышеизложенное, тема, выбранная для написания курсовой работы является актуальной.

Цель данной работы – исследовать методы прогнозирования и рассмотреть их практическое использование в эконометрике.

Задачами данной работы являются:

· Рассмотреть методику применения моделей скользящей средней в эконометрике;

· Изложить методику применения авторегрессивных моделей;

·  Выявить сущность и назначение прогнозирования на основе временных рядов;

· применить напрактике рассмотренные теоретические аспекты применения прогнозирования в эконометрике.

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. Сущность и назначение прогнозирования на основе временных рядов

Рассмотрим особенности разработки прогнозов стационарного процесса – временного ряда, описываемого обобщенной моделью авторегрессии-скользящего среднего порядка (k,m)[3]:

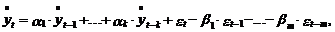
где 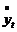 в общем случае представляет собой центрированную переменную с математическим ожиданием m.

Таким образом, данную модель можно переписать в несколько измененном виде:

 (1)

и после очевидных упрощений – в следующем виде:

 (2)

Предположим, что оценки математического ожидания ошибок и оценок коэффициентов модели были получены на основе временного ряда у₁, у₂,..., у_T. 

Оценка точечных прогнозов.

Из выражения (2) следует, что прогнозное значение показателя у_T(1), т. е. на один шаг вперед, может быть определено как условное математическое ожидание переменной у_T   при известном прогнозном фоне, определенном предшествующими значениями у_T, у_T–1   и “эмпирическими” (фактическими) ошибками

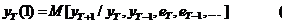(3)

при известных значениях оценок коэффициентов a_i, b_j, i=1,...,k; j=1,...,m.

Подставляя вместо переменных у_t–r, ошибок e _t–r и коэффициентов a_i, b_j   соответствующие значения и оценки, на основе выражения (2) получим

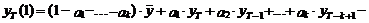
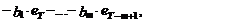(4)

где  – оценка математического ожидания процесса у_t.

Заметим, что в выражении (4) отсутствует ошибка e _T+1, поскольку ее математическое ожидание равно нулю, как и всех ошибок будущих моментов времени, M[e _T+n]=0, n=1,2,... .

Таким образом, прогноз на два шага вперед уде рассчитывается как

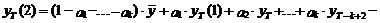
(5)

а прогнозное значение на l шагов вперед, где l>т вообще формируется без учета значений ошибок модели

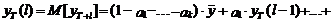
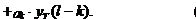(6)

Несложно видеть, что, например,  для моделей авторегрессии АР(k) выражение (6) определяет прогнозное значение для периода упреждения любой глубины. В частности, для модели АР(1) при прогнозировании уже на один шаг вперед получим

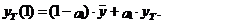(7)

В свою очередь, ошибка модели скользящего среднего первого порядка СС(1) учитывается только в прогнозе на один шаг вперед

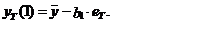(8)

Все следующие прогнозы на основе этой модели рассчитываются по одной и той же формуле[4]:

(9)

Для АРСС(1,1) математическое ожидание прогноза на 1 шаг вперед представляется в следующем виде:

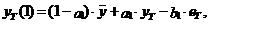  (10)

а на последующие моменты времени уже в виде

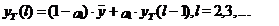(11)

Из изложенного материала вытекает, что разработка прогнозов стационарных процессов, описываемых моделями временных рядов типа АРСС(k, m) для любого периода упреждения l основана на достаточно несложной итеративной процедуре расчета последовательных прогнозных значений у_T(1), у_T(2),..., у_T(l) по построенному варианту модели.

Проблемы оценки дисперсий прогнозов.

Вместе с тем оценка дисперсий таких прогнозов представляет собой достаточно сложную проблему, корректное решение которой в аналитическом виде еще не получено. [5]Раскроем суть этой проблемы. В соответствии с ними, дисперсия прогноза l на точек вперед с использованием модели АРСС(k, m) должна быть определена как математическое ожидание квадрата ошибки прогноза:

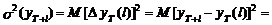
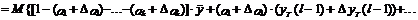
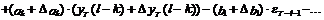
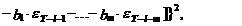(12)

где символ Dх означает ошибку переменной х. В случае детерминированных величин (дисперсия равна нулю) их ошибка должна быть принята равной нулю.

Так, например, дисперсия прогноза процесса, разрабатываемого на один шаг вперед с помощью модели АРСС(1,1) в этом случае должна определяться на основе следующего выражения:

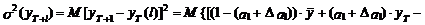
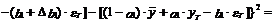
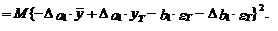(13)

Дисперсия прогноза на два шага вперед в этом случае будет иметь следующий вид:

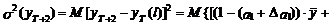
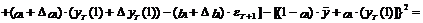
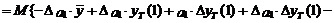
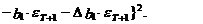(14)

В выражениях (13) и (14) учтено, что ошибка показателей у_T   и  равна нулю, а также, что математическое ожидание ошибки e_T+1  равно нулю.

Теоретически, при известных дисперсиях оценок коэффициентов моделей АРСС(k, m),  их взаимных ковариаций, а также дисперсий предыдущих прогнозных значений у_T(l–r), r=1,2,... и дисперсий ошибки e  с  помощью выражения (12) оценку дисперсии прогноза s²(у_T+l) определить не слишком сложно, хотя ее математическое выражение и будет выглядеть достаточно громоздко. Однако следует иметь в виду, что, если с помощью рассмотренных в главе VI методов дисперсии (и ковариации) прогнозов у_T+l–r, ошибки e, определить возможно, то дисперсии коэффициентов модели оценить можно лишь приблизительно и то, используя достаточно сложные методы. Это вызвано тем, что оценки моделей АРСС(k, m) определяются либо на основе выборочных значений коэффициентов автокорреляции рассматриваемых процессов (уравнения Юла-Уокера, нелинейные методы оценки коэффициентов скользящего среднего[6]), либо с использованием нелинейных методов оценивания.

В первом случае дисперсии оценок ставятся в зависимость от показателей точности выборочных коэффициентов автокорреляции, которые к тому же сами определяются лишь приблизительно (см. главу VI). Так, например, если для модели АР(1) дисперсию параметра a₁, равного r₁,  можно (с известной погрешностью) приблизительно считать равной 1/Т, s²(a₁)=s²(r₁)=1/Т, где r₁  – первый выборочный коэффициент автокорреляции рассматриваемого процесса, то уже для модели АРСС(1,1) этот коэффициент равен a₁=r₂/r₁  и даже при известных дисперсиях оценок коэффициентов автокорреляции r₁ и r₂ показатель s²(a₁) оценить достаточно сложно. При этом с увеличением размерности модели АРСС(р,q) проблема оценки дисперсий ее коэффициентов, а тем более их ковариаций значительно осложняется.

Нелинейные методы оценки параметров модели также в явном виде не позволяют определить их показатели точности.

Оценки дисперсий прогнозов при детерминированных параметрах моделей.

В этой связи, в научной литературе обычно рассматриваются методы оценки дисперсий прогнозов процессов, представленных в виде временных рядов, не учитывающие ошибки оценок коэффициентов, описывающих их моделей. Таким образом, эти методы учитывают специфику моделей с детерминированными параметрами. Очевидно, что эти методы не в полной мере адекватны условиям поставленной задачи. Однако они характеризуются определенной математической строгостью и при небольших ошибках (дисперсиях) коэффициентов моделей позволяют получить относительно точные оценки дисперсий прогнозов, а следовательно, и их доверительных интервалов.

Эти методы можно рассматривать как следствие более общих результатов теории прогнозирования, Г. Валдом, Н.Винером, А. Колмогоровым, П. Уиттлом.[7] В их основе лежит идея представления прогнозного значения рассматриваемого процесса, описываемого моделями типа АРСС(k, m), в виде условного математического ожидания, зависящего от известных в моменты Т, Т–1,... его значений в прошлом, и ошибки, выражаемой текущим и предшествующими значениями “белого шума”. В целях избежания излишней громоздкости рассмотрим эти методы на примере наиболее простых вариантов моделей временных рядов первого порядка.

Модель АР(1).

В соответствии с выражением (1) представим модель АР(1) в виде следующего уравнения:

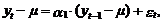
которое для наших целей более удобно представить в следующем виде:

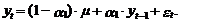(15)

Из выражения (15) вытекает, что прогноз на один шаг вперед, т. е. на момент Т+1, является случайной величиной, определяемой следующим выражением:

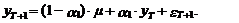(16)

Математическое ожидание этого прогноза имеет следующий вид:

(17)

Ошибка такого прогноза определяется как

(18)

При определении дисперсии прогноза различие между параметром a₁ и его оценкой a₁ во внимание не принимается. В результате имеем

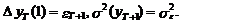(19)

Для момента Т+2 прогноз определяется по следующей схеме:

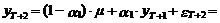
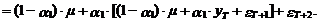(20)

Из выражения (20) следует, что математическое ожидание этого прогноза имеет следующий вид:

а ошибка D у_T(2) равна

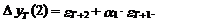(21)

В свою очередь, с учетом независимости e_T+2 и e_T+1 из выражения (21) следует, что дисперсия прогноза на момент Т+2 оценивается согласно следующему выражению:

(22)

Продолжая схему прогнозирования, определенную выражениями (15)-(22) несложно видеть, что прогноз на l шагов вперед на основе модели АР(1) представляется в следующем виде:

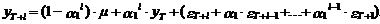(23)

Его математическое ожидание определяется выражением

(24)

а ошибка и ее дисперсия – соответственно выражениями

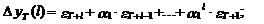(25)

(26)

Из выражений (24), в частности, вытекает, что так как ça₁ç<1, то c ростом l математическое ожидание прогноза стремится к математическому ожиданию стационарного процесса

а дисперсия прогноза стремится к дисперсии процесса

поскольку из выражения (26) следует, что

(27)

Модель СС(1).[8]

Прогнозируя на момент Т+1 на основе модели СС(1)

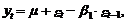
получим следующее прогнозное значение рассматриваемой переменной y:

(28)

Поскольку математическое ожидание ошибки e_T+1 равно нулю, а ее значение в момент времени Т известно, то математическое ожидание такого прогноза равно

(29)

где – оценка ошибки модели в момент Т.

Из (28) и (29) вытекает, что  при неразличимости параметра b₁  и его оценки b₁ ошибка такого прогноза равна e_T+1.

(30)

а его дисперсия –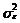

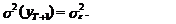(31)

Прогноз на два шага по модели СС(1) определяется выражением

(32)

Его математическое ожидание равно  –

(33)

Ошибка такого прогноза равна

(34)

а ее дисперсия определяется следующим выражением:

(35)

Несложно заметить, что выражение (35) определяет величину дисперсии ошибки прогноза, полученного с использованием модели СС(1), на любое количество шагов вперед, поскольку сама ошибка представляется в следующем виде:

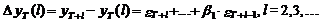(36)

Модель АРСС(1,1).[9]

Модель АРСС(1,1), являющуюся комбинацией рассмотренных выше моделей АР(1) и СС(1), представим в следующем виде:

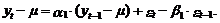
Несложно заметить, что прогнозное значение переменной у_T+1  определяется следующим выражением:

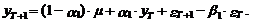(37)

Математическое ожидание такого прогноза с учетом равенства нулю математического ожидания ошибки e_T+1 и известного значения ошибки 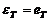  равно

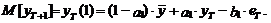(38)

Прогнозируя на момент Т+2, получим следующие выражения, определяющие прогнозное значение рассматриваемой переменной и его математическое ожидание соответственно:

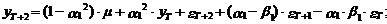(39)(40)

Из выражений (39) и (40) вытекает, что оценка дисперсии прогноза на два шага вперед с использованием модели АРСС(1,1) может быть представлена в следующем виде:

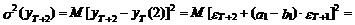
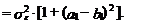(41)

Продолжая последовательно процедуру прогнозирования  на момент Т+l, получим следующие выражения прогнозного значения случайной величины и ее математического ожидания:

(42)

(43)

Соответственно из выражений (42) и (43) вытекает, что оценка дисперсии этой ошибки (дисперсии прогноза) может быть определена следующим образом:

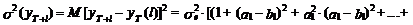
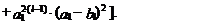(44)

Несложно показать, что l®¥ оценка дисперсии прогноза у_T+l стремится к следующему пределу:

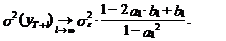(45)

По аналогичной схеме в предположении о детерминированном характере показателей моделей могут быть получены выражения, определяющие оценки дисперсий прогнозов моделей временных рядов и других модификаций, включая модели финансовой эконометрики.

1.2. Методика применения авторегрессивных моделей

Использование моделей авторегрессии при моделировании закономерностей реального стационарного процесса второго порядка, допускающего представление в виде дискретного временного ряда его значений, основано на предположении о том, что текущее значение такого процесса может быть выражено в виде линейной комбинации некоторого количества  предыдущих его значений и случайной ошибки, обладающей свойствами белого шума.[10]

Общий вид модели авторегрессии k-го  порядка – АР(k) может быть выражен следующим уравнением:

(46)

где у_t, у_t–i, i=1,2,... , k – значения переменной у в соответствующие моменты времени; k – порядок модели; a₁,..., a_k  – коэффициенты модели; e_t  – случайная ошибка с нулевым математическим ожиданием, конечной дисперсией и единичной автокорреляционной матрицей, свидетельствующей об отсутствии автокорреляционной связи между рядами ошибки e_t, e_t–1,..., e_t–i,..., т. е. e_t  ~N(0, s_e² ), Cov(e)=s_e² ×E.

Построение модели АР(k) типа (46), адекватной реальному временному ряду у_t, t=1,2,..., Т, предполагает решение двух взаимосвязанных задач: определения рационального порядка модели (величины k) и оценки значений ее коэффициентов. Рассмотрим сначала общие подходы к оценке параметров модели типа (46).

Без ограничения общности будем предполагать, что математическое ожидание ряда у_t   равно нулю, т. е. M[у_t ]=0. В противном случае вместо  переменной у_t   в выражении (46) можно рассмотреть центрированную переменную 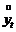, , где – оценка M[у_t ]. Легко видеть, что M[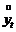 ] = 0.

Из выражения (46) непосредственно следует, что параметры модели a₁,..., a_k    могут быть выражены через коэффициенты автокорреляции. Чтобы показать это, умножим выражение (6.36) под знаком математического ожидания на переменную у_t–i, i=1,2,..., k. Получим

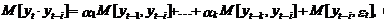(47)

где M[у_t-i, у_t--j] – математическое ожидание произведения двух центрированных переменных у_t–i, у_t–j, представляющих собой их ковариацию g_r, на практике оцениваемую по формуле

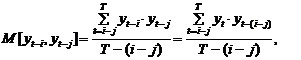(48)

где r=i–j , i ³ j.

В результате для i=1,2,..., k  вместо (47) можно записать

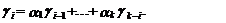(49)

Выражение (49) получено в предположении, что M[у_t-i, e_t]=0 при i>0, так как e_t  – случайная величина со свойствами “белого шума”, не имеющая корреляционной связи с предшествующими моменту t значениями рассматриваемого процесса у_t. Разделив левую и правую части выражения (49) на дисперсию процесса у_t   s_у²=g ₀, получим следующее выражение:

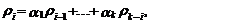(50)

которое связывает коэффициенты автокорреляции процесса у_t  и  коэффициенты модели АР(k).

Подставив в (50) вместо истинных значений коэффициентов автокорреляции r_i    процесса у_t  их выборочные оценки r₁, r₂,..., последовательно для i=1,2,..., k, получим следующую систему линейных уравнений:

(51)

в которой известными являются оценки коэффициентов автокорреляции r₁, r₂,..., r_k, а неизвестными – оценки коэффициентов модели АР(k) a₁ , a₂ ,..., a_k.

Систему (51)  называют уравнениями Юла-Уокера, а полученные на ее основе значения a₁, a₂,..., a_k   – оценками коэффициентов модели авторегрессии АР(k) Юла-Уокера. Напомним, что эти оценки могут быть получены, например, с использованием определителей, либо на основе векторно-матричной формы записи системы (51).

На основе определителей оценки Юла-Уокера получают в следующем виде:

(52)

где D – определитель системы (6.41).

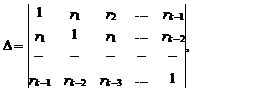(53)

D_i  – определитель, получаемый  из определителя D путем замены его i-го столбца на столбец, состоящий из коэффициентов автокорреляции, образующих левую часть системы (51) – r₁,   r₂,..., r_k.

В векторно-матричной форме записи систему (51) можно переписать в следующем виде:

r = R×a,                                         (54)

где r – вектор-столбец известных оценок коэффициентов автокорреляции с первого по k-й включительно, r=(r₁,   r₂, ..., r_k)¢;    a  – вектор-столбец неизвестных оценок параметров модели, a=(a₁, a₂,..., a_k)¢; R – матрица, составленная из оценок коэффициентов автокорреляции, определитель которой выражен формулой (53).

Непосредственно из выражения (54) вытекает, что неизвестные оценки коэффициентов модели авторегрессии определяются как

a  = R^–1×r.                                         (55)

Теоретически оценки Юла-Уокера[11] должны обладать свойствами несмещенности и эффективности. Однако, на практике, в моделях авторегрессии большого порядка эти свойства могут не подтверждаться. Особенно это относится к свойству несмещенности. Как и в моделях с лаговыми зависимыми переменными, смещенность в оценках коэффициентов моделей авторегрессии может быть обусловлена существующей зависимостью между сдвинутыми рядами рассматриваемой переменной у_t–1, у_t–2  и ошибкой e_t. Этой возможной зависимостью при построении системы уравнений Юла-Уокера обычно пренебрегают, полагая  e_t   белым шумом.

Неэффективность оценок может быть вызвана плохой обусловленностью матрицы R, что, как правило, является свидетельством зависимости уже между рядами у_t–1, у_t–2,... .

Вместе с тем, при небольших порядках модели (k =1,2,3) оценки Юла-Уокера обычно являются достаточно “хорошими”. В крайнем случае их можно рассматривать как первое приближение к “оптимальным” оценкам, которые могут быть получены путем уточнения оценок Юла-Уокера на основе использования более мощных методов оценивания, например, нелинейных.

Качество оценок Юла-Уокера может быть проверено путем исследования свойств ряда ошибки e_t, t=1,2,..., Т. Если ее свойства близки к характеристикам “белого шума”, то оценки Юла-Уокера можно считать “достаточно хорошими”. Об этом, в частности, может свидетельствовать критерий Дарбина-Уотсона, значение которого должно лежать примерно в интервале от 1 до 3[12].

Для этих целей могут использоваться и другие мощные критерии, например, Бартлетта, Тейла.

Обоснование целесообразности применения моделей авторегрессии.  Целесообразность использования моделей авторегрессии в анализе закономерностей временного ряда обычно устанавливается на основе сопоставления двух дисперсий – дисперсии исходного процесса s_у²  и дисперсии ошибки модели s_e². Для того чтобы выявить взаимосвязь между двумя этими характеристиками положим, что  в формуле (49) i=0. Тогда это выражение можно переписать в следующем виде:

(56)

где g₀=s_у², g_i     – i-й  коэффициент автоковариации.

Последнее слагаемое в правой части выражения (56) получено путем замены в выражении (47) в произведении M[y_t××e_t] переменной y_t  на ее модель (46). Поскольку ряды  у_t–1,..., у_t–k    и e_t   являются независимыми,  то это произведение оказывается равным s_e². Далее, поскольку g_i =r_i×g₀, то выразив все g_i, i=1,2,..., k  через g₀  и перенеся слагаемые с g₀  в левую часть, из выражения (56) получим

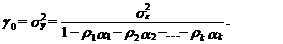(57)

Подставив в (57) вместо r_i  значения оценок коэффициентов автокорреляции r_i    и вместо параметров модели a_i   их оценки  а_i, i=1,2,... , k, найдем величину соотношение между дисперсией процесса s_у²  и дисперсией ошибки описывающей этот модели авторегрессии (белого шума) s_e².

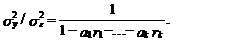(58)

Модель авторегрессии считается “достаточно хорошей”, если  s_у²>>s_e², т. е. когда дисперсия ошибки модели много меньше дисперсии процесса. В этом случае использование модели при описании процесса y_t  позволяет значительно снизить его неопределенность, выражаемую через дисперсию s_у². Здесь также следует отметить, что в моделях временных ярдов нельзя ожидать значительного уменьшения дисперсии ошибки s_e²   по сравнению с дисперсией процесса s_у², как это имело место в моделях “классической” эконометрики, где отношение s_у²/s_e²  нередко превосходит несколько десятков.

Чтобы показать это, рассмотрим свойства наиболее часто используемых в практике финансовых исследований моделей авторегрессии первого и второго порядков.

Модели АР(1) и АР(2).[13]

Модель авторегрессии первого порядка АР(1) записывается в следующем виде:

(59)

Легко видеть, что система Юла-Уокера в этом случае сводится к одному уравнению, непосредственно определяющему оценку a₁ коэффициента a₁

a₁=r₁.                                          (60)

Из выражения (58) вытекает, что

(61)

Поскольку  ½r₁½<1, то из (61) следует, что, например, при r₁=0,9  s_e²»0,2×s_у². Это означает, что использование расчетных значений процесса y_t, определяемых по формуле 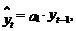 вместо среднего значения временного ряда  позволит повысить точность предсказания его значений в пять раз (если в качестве меры точности рассматривать показатель дисперсии).  В этом случае соотношение между среднеквадратическими ошибками s_у и s_e  составит примерно 2,3. Из выражения (61) легко также видеть, что с ростом абсолютного значения r₁  точность описания процесса y_t   моделью  авторегрессии первого порядка увеличивается, а с его снижением – падает.

Модель авторегрессии второго порядка – АР(2) представляется в виде следующего уравнения:

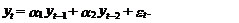(62)

Система уравнений Юла-Уокера в этом случае состоит из двух уравнений

(63)

Выразив a₁  и a₂ через коэффициенты автокорреляции с использованием, например, метода определителей (52), получим

(64)

Из выражения (58) непосредственно вытекает, что в этом случае соотношение между дисперсиями исходного процесса y_t  и ошибкой модели e_t  определяется следующим выражением:

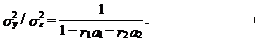(65)

На практике и в случае АР(2) соотношение между s_у² и s_e²    обычно не превосходит 5:1. В этом смысле следует отметить, что по сравнению с эконометрическими моделями, где это соотношение достигает 50 к 1 и даже 100 к 1, модели авторегрессии, на первый взгляд, не обладают высокой точностью описания рассматриваемых процессов. Однако не следует забывать, что в “классической” эконометрике зависимая переменная y_t  не обладает  свойством стационарности и она характеризуется гораздо большей изменчивостью (и, как следствие, дисперсией) по сравнению со стационарным временным рядом. Поэтому адекватные рассматриваемому процессу многофакторные эконометрические модели могут значительно уменьшить остаточную изменчивость (дисперсию ошибки) по сравнению с исходной (дисперсией процесса), но при этом изменчивость ошибки может оставаться относительно большой.

Модели же авторегрессии, как и другие модели стационарных временных рядов, как бы уточняют” исходный процесс y_t, как правило, благодаря свойству стационарности не отличающийся значительной изменчивостью. Вследствие этого у этих моделей имеется лишь незначительный резерв для уменьшения исходной дисперсии s_у²  по сравнению с многофакторными эконометрическими моделями, описывающими нестационарные процессы.

Автокорреляционная функция моделей авторегрессии.

По аналогии с реальными стационарными процессами, автокорреляционные функции могут быть сформированы и для их теоретических аналогов – моделей авторегрессии.[14] Заметим, что значения коэффициентов автокорреляции модели k-го порядка связаны между собой соотношением (50). Несложно заметить, что для модели авторегрессии первого порядка это соотношение приводит к следующей зависимости между коэффициентами автокорреляции:

(66)

В самом деле, из выражения (59)) для i=2 имеем r₂=a₁r₁  и, учитывая, что a₁=r₁, получим r₂=r₁², аналогично, для i=3 имеем r₃=a₁r₂=r₁³  и т.д. Если учесть, что ôr₁ô<1, то нетрудно заметить, что модули значений коэффициентов автокорреляции модели АР(1) авторегрессии уменьшаются по экспоненте с ростом сдвига i.

Можно показать, что поскольку модель авторегрессии второго порядка является стационарным процессом, то ее автокорреляционная функция представляет собой либо затухающую экспоненту, либо затухающую синусоиду. В первом случае абсолютные значения коэффициентов автокорреляции r_i    с ростом i  уменьшаются согласно следующей зависимости:

(67)

где d – положительный коэффициент экспоненциальной зависимости, отличный от единицы, d ¹1.

Заметим, что для модели АР(1) этот коэффициент равен единице (см. выражение (66)).

Во втором случае значения коэффициентов r_i  аппроксимируются функцией следующего вида:

(68)

где f и F – параметры синусоиды (частота и фаза соответственно), рассчитываемые на основе значений коэффициентов модели. В частности,

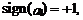если a₁ >0 и если a₁ <0.

1.3. Методика применения моделей скользящей средней в эконометрике

В моделях скользящего среднего текущее значение стационарного случайного процесса второго порядка y_t   представляется в виде линейной комбинации текущего и прошедших значений ошибки e_t, e_t–1, e_t–2,... , по своим свойствам соответствующей “белому шуму”[15]. Такое представление может быть выражено следующим уравнением (модель скользящего среднего порядка m – СС(m)):

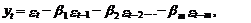(69)

где b₁, b₂,... , b_m   – параметры модели.

В соответствии с определением белого шума ошибка e_t  характеризуется следующими свойствами:

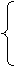M[e_t]=0, D(e_t)=s_e²=const,

  g_i=M[e_t , e_t–i  ] =     (70)

Вследствие этого и автокорреляционная функция белого шума имеет очень простую форму

r_i^(e)=1, i=0; r_i^(e)=0, i¹0.                        (71)

С учетом свойств ошибки e_t   несложно построить автокорреляционную функцию модели СС(т), определяемой выражением (69). Ее коэффициент ковариации i-го порядка определяется следующим образом:

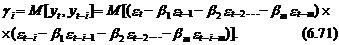(72)

При i=0 выражение (72) представляет собой дисперсию процесса y_t, которая в силу свойства (70) выражается через коэффициенты модели СС(т) b_i, i=1, 2,..., т; и дисперсию ошибки s_e² следующим образом:

(73)

Для i=1 из (73) получим, что первый коэффициент ковариации определяется выражением

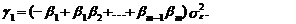(74)

Для произвольного i имеем

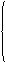
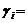
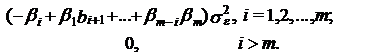 (75)

Из соотношения (75) вытекает, что автокорреляционная функция  модели СС(т) становится равной нулю после задержки т (обрывается на задержке т).

С учетом выражений (73) и (75) несложно также заметить, что коэффициенты автокорреляции модели скользящего среднего т-го порядка – СС(т) определяются через ее параметры b_i, i=1, 2,..., т; следующим образом:

  (76)

Система из т уравнений (76), сформированных для  i=1,2,..., т может  служить основой для получения оценок b₁, b₂,... , b_m  неизвестных параметров модели СС(т) – b₁, b₂,... , b_m. Для этого необходимо подставить в каждое ее уравнение вместо значений коэффициентов автокорреляции r₁,..., r_m  рассматриваемого процесса y_t  их рассчитанные оценки r₁,..., r_m.

Однако в отличие от уравнений Юла-Уокера эта система нелинейная и ее решение требует использования специальных итеративных процедур расчетов за исключением наиболее простой модели СС(1). Она представляется следующим выражением:

(77)

Из (73) следует, что дисперсии процесса  s_у²  и ошибки этой модели s_e²   связаны следующим соотношением:

(78)

а ее единственный отличный от нуля первый коэффициент автокорреляции выражается через коэффициент модели как

(79)

Из соотношения (79) несложно получить квадратическое уравнение относительно оценки b₁  неизвестного параметра b₁

(80)

где r₁  – оценка коэффициента автокорреляции первого порядка процесса y_t, т. е. r₁.

В свою очередь, из (80) следует, что существуют два решения этого уравнения, связанные между собой следующим соотношением:

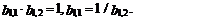(81)

Условию стационарности процесса y_t  удовлетворяет только решение b по абсолютной величине меньшее единицы. Оно может быть получено из следующего выражения:

(82)

при условии, что

(83)

Из (83) следует, что модели скользящего среднего первого порядка могут применяться только для описания процессов с автокорреляционной функцией, обрывающейся после первой задержки и коэффициентом автокорреляции по абсолютной величине не превышающем 0,5. Из соотношения (83) также вытекает, что данные модели способны лишь незначительно уточнить рассматриваемый процесс y_t, поскольку согласно (78) максимальное соотношение между его дисперсией и дисперсией ошибки не превосходит 1,25

s_у²/s_e²< 1,25 ,                            (84)

т. е. относительный выигрыш в точности не превосходит 25% для дисперсий (чуть более 11% для среднеквадратических ошибок).

В заключение этого раздела приведем основные результаты для модели скользящего среднего второго порядка – СС(2). Ее уравнение в общем виде записывается следующим образом:

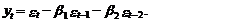(85)

Из (73) непосредственно вытекает, что дисперсии процесса s_у²  и ошибки s_e ²  связаны следующим соотношением:

(86)

а ее автокорреляционная функция определяют значения коэффициентов автокорреляции, связанные с параметрами модели следующими соотношениями:

                         (87)

из которых могут быть найдены оценки коэффициентов модели b₁ и b₂  при известных оценках коэффициентов автокорреляции процесса y_t  – r₁ и r₂.

2. ПРАКТИЧЕСКАЯ ЧАСТЬ

Многие финансово-экономические показатели наряду с устойчивой тенденцией к росту или уменьшению подвержены сезонным колебаниям. Такие процессы удовлетворительно моделируются временными рядами, включающими в себя как тренд, так и сезонную компоненту (тренд - сезонными временными рядами). Примером такого экономического показателя может служить стоимость акции, растущая в цене в течение ряда лет, по которой ежегодно выплачиваются (например, в начале года) дивиденды. Так как стоимость акции из года в год растет, мы имеем восходящий  долгосрочный тренд. Однако, в начале  года стоимость акции ниже, чем в конце предыдущего года, так как ее стоимость  к концу года включает в себя накопившиеся за год дивиденды. Их получит владелец ценной бумаги, после чего дивиденды уже не входят в стоимость акции, и цена ее уменьшается.

 Для краткосрочного прогнозирования таких процессов можно использовать адаптивные модели с сезонной компонентой,  например, модель Хольта-Уинтерса.[16]

2.1. Построение модели Хольта-Уинтерса.

Рассмотрим данный метод на примере роста стоимости акции. Временной ряд, характеризующий стоимость акции за 16 кварталов (4 года) приведен в табл. 2.1. Нас интересуют прогнозные значения цен на эти акции в 1-4 кварталах пятого года.

Таблица 2.1. Цена акции за 16 кварталов (4 года)

Будем считать, что зависимость между компонентами тренд-сезонного временного ряда мультипликативная. Мультипликативная модель Хольта-Уинтерса с линейным ростом имеет следующий вид:

Y_p(t+k)   =   [ a(t) + k*b(t) ] * F(t+k-L)                                                (2.1)

где  k – период упреждения,

    Y_p(t)- расчетное значение экономического показателя для t-го периода;

    a(t) , b(t)  и  F(t) коэффициенты модели, они адаптируются, уточняются   по мере перехода от членов ряда с номером t-1 к t;

   F(t+k-L) – значение коэффициента сезонности того периода, для         которого рассчитывается экономический показатель. L – период сезонности (для квартальных данных L=4, для месячных  L=12). Таким образом, если по формуле 3.1 рассчитывается значение экономического показателя, например, за второй квартал, то F(t+k-L)  как  раз будет коэффициентом сезонности второго квартала предыдущего года.

Уточнение (адаптация к новому значению параметра  времени t) коэффициентов модели производится с помощью формул:

         a(t) =1* Y(t)/F(t-L) + (1 - 1) * [ a(t-1)+b(t-1) ]                      (2.2)

        b(t) =3* [ a(t) – a(t-1) ]  +  (1 - 3) * b(t-1)                              (2.3)

        F(t)=2*Y(t)/a(t)+(1-2)*F(t-L)                                                  (2.4)

Параметры сглаживания a1 , a2  и  a3 подбирают путем перебора с таким расчетом, чтобы расчетные данные наилучшим образом соответствовали фактическим (то есть чтобы обеспечить удовлетворительную адекватность и точность модели).

Из формул 2.1 – 2.4 видно, что для расчета a(1)  и b(1) необходимо оценить значения этих коэффициентов для предыдущего период времени (то есть для t=1-1=0). Значения a(0)  и b(0)  имеют смысл этих же коэффициентов  для  четвертого квартала года, предшествующего первому году, для которого имеются данные в табл. 3.1.

Для оценки начальных значений  a(0) и  b(0)  применим линейную модель к первым 8 значениям Y(t)   из табл. 3.1. Линейная модель,  имеет вид:

Y_p(t)   =   a(0) + b(0)*t                                                                      (2.5)

Метод наименьших квадратов дает возможность определить коэффициенты линейного уравнения a(0) и  b(0) по формулам (2.6-2.9):

                                               (2.6)

a(0) = Y_cp  - b(0)*t_ср                                                    (2.7)

Применяя линейную модель к первым 8 значениям  ряда  из таблицы 2.1. (то есть к данным за  первые 2 года), находим значения  a(0)= 300,05, b(0)= 8,60.

Уравнение (2.5) с учетом полученных коэффициентов имеет вид: Y_p(t) = 300,05 + 8,60*t. Из этого уравнения находим расчетные  значения Y_p(t) и сопоставляем их с фактическими значениями (см. табл.3.2). Такое сопоставление позволяет оценить приближенные значения  коэффициентов  сезонности 1 – 4 кварталов F(-3),  F(-2), F(-1)   и F(0) для года, предшествующего первому году, по которому имеются данные в табл. 2.1.  Эти значения  необходимы для расчета коэффициентов сезонности первого года F(1), F(2), F(3), F(4)   и других параметров модели Хольта-Уинтерса по формулам 2.1-2.4.

Таблица 2.2. Сопоставление фактических данных Y(t) и рассчитанных по линейной  модели. значений Y_p(t)

Коэффициент сезонности есть отношение фактического значения экономического показателя к рассчитанному по линейной модели. Поэтому в качестве оценки коэффициента сезонности первого квартала  F(-3) может служить отношение фактических и расчетных значений Y(t) первого квартала первого года, равное Y(1)/Y_p(1)   и такое же отношение для первого квартала второго года (то есть за пятый квартал t=5) Y(5)/Y_p(5). Для  окончательной, более точной оценки этого коэффициента  сезонности можно использовать среднее арифметическое  значение  этих двух величин

F(-3)=[Y(1)/Y_p(1)+Y(5)/Y_p(5)]/2=[304/308,67+323/343,05]/2= =[0,9849+0,9416]/2=0,9633

Аналогично находим  оценки коэффициенты сезонности для второго, третьего и четвертого кварталов:

F(-2) =  [ Y(2)/Y_p(2)  + Y(6)/Y_p(6) ] / 2 =  0,9907

F(-1) =  [ Y(3)/Y_p(3)  + Y(7)/Y_p(7) ] / 2 =  1,0191

F(0)  =  [ Y(4)/Y_p(4)  + Y(8)/Y_p(8) ] / 2 =  1,0271

Oценив значения   a(0), b(0), а также F(-3), F(-3), F(-3) и F(0), можно перейти к построению адаптивной мультипликативной модели Хольта-Уинтерса с помощью формул (2.1-2.4).

Путем перебора возможных значений параметров сглаживания, было установлено, что лучшими являются a1 = 0,3; a2 = 0,6; a3 = 0,3.

Рассчитаем значения Y_p(t), a(t), b(t) и F(t)  для t=1.

Из уравнение 3.1, полагая  t=0, k=1  находим  Y_p(1):  

Y_p(0+1)=Y_p(1)=[a(0)+1*b(0)]*F(0+1-4)=[a(0)+1*b(0)]*F(-3)=

 =[ 300,05+ 1* 8,60 ] * 0,9633 = 297.32

Из уравнение 2.2-2.4, полагая  t=1  находим:  

a(1)=1*Y(1)/F(-3)+(1-1)*[a(0)+b(0)]=0.3*304/0,9633+(1-0.3)*[300,05+8,60 ]=310.73

b(1)=3*[a(1)–a(0)]+(1-3)*b(0)=0.3*[310.73-300,05]+(1-0.3)*8,60=9.22

F(1)=2*Y(1)/a(1)+(1-2)*F(-3)=0.6* 304/310.73+(1-0.6)* 0,9633=0.9723

Аналогично рассчитаем значения Y_p(t), a(t), b(t) и F(t) для t=2

Yp(2)=[ a(1) + 1 * b(1) ]*Fo(-2)=[ 310.73+1*9,22 ] * 0,9907=316.97

a(2)=1*Y(2)/F(-2)+(1-1)*[a(1)+b(1)]=0.3*320/0,9907+0.7*[310,73+9.22]=320.87

b(2)=3*[a(2)–a(1)]+(1-3)*b(1)=0.3*[ 320.87-310.73]+0.7* 9.22=9.50

F(2)=2*Y(2)/a(2)+(1-2)*Fo(-2)=0.6* 320/320.87+0.4* 0,9907=0.9947

          для    t=3

Yp(3)=[ a(2)+1 * b(2)]*Fo(-1)=[320.87+1*9,50 ]*1.0191=3369

a(3)=1*Y(3)/F(-1)+(1-1)*[a(2)+b(2)]=0.3*334/1.0191+0.7*[320,87+9.50]=329.58

b(3)=3*[a(3)–a(2)]+(1-3)*b(2)=0.3*[ 329.58-320.87]+0.7* 9.50=9.26

F(3)=2*Y(3)/a(3)+(1-2)*F(-1)=0.6*334/329.58+(1-0.6)*1.0191=1.0157

       для    t=4

Yp(4)=[ a(3)+1*b(3)]*F(0)=[329.58+1*9,26 ]*1.0271=348.02

a(4)=1*Y(4)/F(0)+(1-1)*[a(3)+b(3)]=0.3*347/1.0271+0.7*[329,58+9.26]=338.54

b(4)=3*[a(4)–a(3)]+(1-3)*b(3)=0.3*[338.54-329.58]+0.7* 9.26=9.17

F(4)=2*Y(4)/a(4)+(1-2)*F(0)=0.6* 347/338.54+0.4*1.0271=1.0258

        для    t=5

Yp(5)=[a(4)+1*b(4)]*F(1)=[338.54+ 1*9,17]*0.9723=338.08

Обратим внимание на то, что здесь и в дальнейшем используются коэффициенты сезонности F(t-L), уточненные в предыдущем году (L=4).

a(5) =1* Y(5)/F(1)+(1-1)*[a(4)+b(4)]=0.3*323/0.9723+(1-0.3)*[338.54+9.17 ]=343.06

b(5) =3*[a(5)–a(4)] +(1-3)*b(4)=0.3*[343.06-338.54]+(1-0.3)*9.17=7.77

F(5)=2*Y(5)/a(5)+(1-2)*F(1)=0.6* 323/343.06+(1-0.6)* 0.9723=0.9538

Продолжая аналогично для t=6,7,8,…,16, строят модель Хольта-Уинтерса (см. табл. 2.3). Максимальное значение t , для которого можно находить коэффициенты модели,  равно количеству имеющихся данных по экономическому показателю Y(t). В нашем примете данные приведены за 4 года, то есть за 16 кварталов. Максимальное значение t равно 16. Ошибкой является попытка студента рассчитать или использовать коэффициенты a(t), b(t) для t > 16.

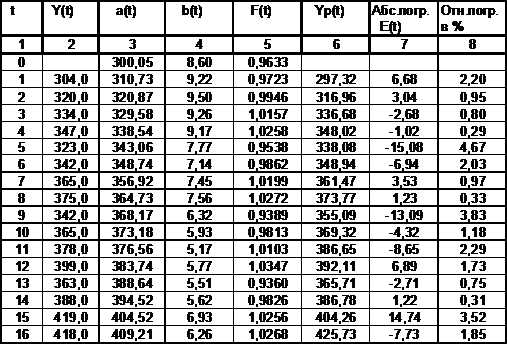
Таблица 2.3. Модель Хольта-Уинтерса

2.2. Проверка качества модели

Для того, чтобы модель была качественной уровни остаточного ряда E(t) (разности Y(t)-Y_p(t) между фактическими и расчетными значениями экономического показателя) должны удовлетворять определенным условиям (точности и адекватнсти). Для проверки выполнения этих условий составим таблицу 2.4.

1. Проверка точности модели.

Будем считать, что условие точности выполнено, если относительная погрешность (абсолютное значение отклонения abs{E(t)} поделенное на фактическое значение Y(t) и выраженное в процентах 100%*abs{E(t)}/Y(t) ) в среднем не превышает 5%.  Суммарное значение относительных погрешностей (см. гр.8 табл.2.3.) составляет 27.7, что дает среднюю величину 27.7/16 = 1.73%.

         Следовательно, условие точности выполнено.

2. Проверка условия адекватности.

Для того, чтобы модель была адекватна исследуемому процессу  ряд остатков E(t) должен обладать свойствами 

а) случайности;

б) независимости последовательных уровней;

в) нормальности распределения.[17]

Проверка случайности уровней. Проверку случайности уровней остаточной компоненты (гр. 2 табл. 2.4) проводим на основе критерия поворотных точек. Для этого каждый уровень ряда E(t) сравниваем с двумя соседними. Если он больше (либо меньше) обоих соседних уровней, то точка считается поворотной и  в гр. 3 табл. 3.4 для этой строки ставится 1, иначе в гр. 3  ставится 0. В первой и последней строке гр. 3 табл. 3.4 ставится прочерк или иной  знак, так как у этого уровня нет двух соседних уровней.

Таблица 2.4. Промежуточные расчеты для оценки  адекватности модели[18]

Общее число поворотных точек в нашем примере равно р = 10.

Рассчитаем   значение  q:

    Функция int означает, что от полученного значения берется только целая часть. При N = 16   

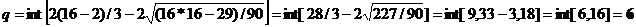
Если количество поворотных точек р больше q, то условие случайности уровней выполнено. В нашем случае р = 10,  q = 6, значит условие случайности уровней ряда остатков выполнено.

Проверка независимости уровней ряда остатков (отсутствия автокорреляции). Проверку проводим двумя методами:

а) по d-критерию Дарбина-Уотсона;

б) по первому коэффициенту автокорреляции r(1).

Проверка по d-критерию Дарбина-Уотсона. Для проверки по d-критерию Дарбина-Уотсона рассчитаем значение d

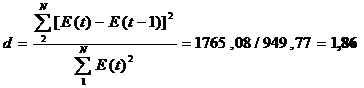
Примечание. В случае если полученное значение больше 2, значит имеет место отрицательная автокорреляция. В таком случае величину d  уточняют, вычитая полученное значение из 4.

Полученное (или уточненное) значение d  сравнивают с табличными значениями d1и d2. Таблицу значений d1 и  d2 можно найти, например,  в литературе[19]. Для нашего случая d1=1.08, а d2=1.36.

Если   0<d<d1, то уровни автокоррелированы, то есть зависимы, модель неадекватна;

Если d1<d<d2, то критерий Дарбина –Уотсона  не  дает   ответа на вопрос о независимости уровней ряда остатков. В таком случае необходимо воспользоваться другими критериями (например, проверить независимость уровней по первому коэффициенту автокорреляции).

Если  d2<d<2 , то уровни ряда остатков являются независимыми.

В нашем случае это условие выполнено, так как 1.36< 1.86<2, следовательно, уровни ряда E(t) независимы.

Проверка по первому коэффициенту автокорреляции r(1).

Рассчитаем r(1)  по формуле

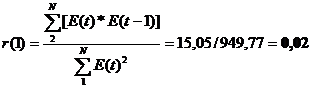
Если модуль рассчитанного значения первого коэффициента автокорреляции меньше критического значения | r(1) |  <  r_таб , то уровни ряда остатков независимы. Таблицу значений r_таб  можно найти, например, в[20]. Для нашей задачи критический уровень r_таб=  0,32. Имеем:

| r(1) | = 0,02  <  r_таб  = 0,32       значит уровни независимы.

Проверка соответствия ряда остатков нормальному распределению определяем по RS – критерию. Рассчитаем значение RS:

                         RS = ( E_max – E_min ) / S 

где E_max -  максимальное значение уровней ряда остатков E(t)

       E_min - минимальное значение уровней ряда остатков E(t) (см. гр. 2 табл. 2.4.)

S - среднее квадратическое отклонение

E_max =14,74   E_min = - 15.08 ,   E_max – E_min  = 14,74-(-15,08) = 29,82

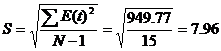
RS =29,82/7.96 = 3.75

Полученое значение  RS сравнивают с табличными значениями, которые зависят от количества точек N и уровня значимости. Таблицу значений границ RS-критерия можно найти в литературе [2, стр. 134]. Для N=16 и 5% уровня значимости значение RS  для нормального распределения должно находиться в интервале от 3,00 до 4,21

Так как 3,00 < 3,75 < 4,21,     полученное  значение RS попало в заданный интервал. Значит,  уровни ряда остатков подчиняются нормальному распределению.

Таким образом, все условия адекватности и точности выполнены. Следовательно, можно говорить об удовлетворительном качестве модели и возможности проведения прогноза показателя Y_p(t) на 4 квартала вперед.

2.3. Расчет прогнозных значений экономического показателя

Составим  прогноз на  4 квартала вперед (т.е. на 1 год, с t=17 по t=20). Максимальное значение t, для которого могут быть рассчитаны коэффициенты a(t), b(t)  определяется количеством исходных данных и равно 16. Рассчитав значения a(16) и b(16) (см. табл.3.3), по формуле 3.1 можно определить прогнозные значения экономического показателя Y_p(t).  Для t=17 имеем:

Y_p(17)=Y_p(16+1)=[a(16)+1*b(16)]*F(16-+1-4)=[a(16)+1*b(16)]*F(13)=

 = [ 409,21 + 1 * 6.26]* 0,9360   =  388,9

Аналогично находим Y_p(18), Y_p(19) и  Y_p(20)

Y_p(18)=Y_p(16+2)=[a(16)+2*b(16)]*F(16-+2-4)=[a(16)+2*b(16)]*F(14)=

 = [409,21 + 2 * 6.26] *0,9826    =  414,4

Y_p(19)=Y_p(16+3)=[a(16)+3*b(16)]*F(16-+3-4)=[a(16)+3*b(16)]*F(15)=

= [409,21 + 3 * 6.26] * 1,0256   = 438,9

Y_p(20)=Y_p(16+4)=[a(16)+4*b(16)]*F(16-+4-4)=[a(16)+4*b(16)]*F(16)=

 = [409,21 + 4 * 6.26 ] * 1,0268   = 445,9

В приложении 1 проводится сопоставление фактических и расчетных данных. Здесь же показаны прогнозные значения цены акции на 1 год вперед. Из рисунка приложения 1 видно, что расчетные данных хорошо согласуются с фактическими, что говорит об удовлетворительном качестве прогноза.

ЗАКЛЮЧЕНИЕ

В заключение данного курсового проекта, можно сделать выводы.

Таким образом, при эконометрическом исследовании имеют место две стороны проблемы обеспечения высокого качества  его результатов – качественная и количественная. Качественная заключается в установлении соответствия между построенной эконометрической моделью и лежащей в ее основе концепцией, а количественная – в точности  аппроксимации (подгонки) имевшихся количественных и качественных характеристик рассматриваемых процессов данными модельных расчетов.

В конкретных научных исследованиях “концептуальные” и собственно “вычислительные”, прикладные аспекты эконометрии нередко отделяются друг от друга. В каждом из них имеют место свои проблемы, нерешенные задачи. Основной задачей “вычислительной” эконометрии является собственно построение адекватной тенденциям рассматриваемых процессов эконометрической модели. Исследованию проблем построения таких моделей в данной работе и будет уделено основное внимание.

Построение эконометрической модели является центральной проблемой любого эконометрического исследования, поскольку ее “качество” непосредственно  определяет достоверность и обоснованность результатов анализа тенденций развития, прогнозов рассматриваемых социально-экономических процессов, а также вытекающих из них выводов, в том числе и по вопросам разработки необходимых управленческих мероприятий.

В эконометрических исследованиях обычно предполагается, что закономерности моделируемого процесса складываются под влиянием ряда других явлений, факторов.

СПИСОК ЛИТЕРАТУРЫ

1. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник для вузов. М.: ЮНИТИ, 1998.

2. Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление/Пер. в анг./ – М.: Мир, 1974.

3. Грубер Й. Эконометрия 1: Введение во множественную регрессию и эконометрию. Ч.1,2,3. Б.м.: Б.и., 1993.

4. Джонстон Дж. Эконометрические методы. М.: Статистика, 1980.

5. Доугерти К. Введение в эконометрику. М.: ИНФРА – М., 1997.

6. Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2-х кн. М.: Финансы и статистика, 1987-88.

7.  Исследование операций в экономике: Учеб. Пособие для вузов/ Н.Ш. Кремер, Б.А. Прутко, И.М. Тришин, М.Н. Фридман; Под ред. Проф. Н.Ш. Кремера. – М.: ЮНИТИ, 2004. – 407 с.

8. Кейн Э. Экономическая статистика и эконометрика. М.: Статистика, 1977.

9. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика: Начальный курс. М.: Дело, 2000.

10. Математическое программирование/ Под ред. Проф. Н.Ш. Кремера. – М.: Финстатинформ, 1995.

11. Уотшем Т. Дж, Паррамоу К. Количественные методы в финансах. М.: ЮНИТИ, 1999.

12. Ферстер Э., Ренц Б. Методы регрессионного и корреляционного анализа: Руководство для экономистов. М.: Финансы и статистика, 1983.

ПРИЛОЖЕНИЯ

Приложение 1

Сопоставление расчетных (ряд 1) и фактических (ряд 2) данных