МЕТОДИЧЕСКИЕ ПОСОБИЕ ПО РЕШЕНИЮ ЗАДАЧ ГЕОМЕТРИИ МЕТОДОМ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ ДЛЯ РАЗВИТИЯ ГЕОМЕТРИЧЕСКИХ УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ АКАДЕМИЧЕСКИХ ЛИЦЕЕВ
МИНИСТЕРСТВО НАРОДНОГО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
КОКАНДСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ имени МУКИМИ
УСТАДЖАЛИЛОВА ХУРШИДА АЛИЕВНА
МЕТОДИЧЕСКИЕ ПОСОБИЕ ПО РЕШЕНИЮ ЗАДАЧ
ГЕОМЕТРИИ МЕТОДОМ ГЕОМЕТРИЧЕСКИХ ПРЕОБРАЗОВАНИЙ ДЛЯ РАЗВИТИЯ ГЕОМЕТРИЧЕСКИХ
УМЕНИЙ И НАВЫКОВ УЧАЩИХСЯ АКАДЕМИЧЕСКИХ ЛИЦЕЕВ
КОКАНД 2011
|
Рецензенты
|
Канд.пед.наук, ст. пр. кафедры «Теория и методика
изучения математики» ТДПУ им. Низами Бакирова А.
Ст.пр. кафедры «Математика-информатика» Сувонов О.
|
Переход на новые этапы экономического
развития нашего общества выявляет много нерешенных вопросов образовательного
характера. Геометрическое образование учащихся должно соответствовать
изменяющейся жизни общества. В сложившейся сейчас
системе математического образования геометрическая
составляющая уже сформирована и изменение структуры курса математики позволило
укрепить её. Геометрическая ветвь
математического образования должна
обеспечить формирование и развитие пространственного
мышления учащихся, интуицию на образы, конструкции, методы,
свойства; развитие геометрических
умений и навыков: умения анализировать и
синтезировать, конструктивно-геометрические,
вычислительные, метрические, умения проводить доказательные рассуждения и т.д.
Следовательно, мы считаем необходимым, обратить внимание на выбор методов и
приемов решения задач на уроках геометрии в лицее, так как именно в процессе решения задач геометрии
развиваются геометрические умения и навыки учащихся. В качестве одного из таких
методов предлагаем метод геометрических преобразований.
Изучение геометрических преобразований не только способствует созданию
более правильных и более современных взглядов на само содержание математики, но
указывает также новые методы решения содержательных геометрических задач,
чрезвычайно важные не только для самой математики, но и для ее приложений.
Кроме того, геометрические преобразования дают представления о фигуре, как о
множестве точек и преобразование, как о своеобразной геометрической функции,
что развивает геометрические умения и навыки учащихся лицея, связывая их с
алгеброй, а также растут их пространственные представления и развивается
логическое мышление [3].
Преобразования плоскости во многих случаях позволяют
экономно и изящно решать задачи на построение, вычисление и доказательство.
При решении задач методом геометрических преобразований
развиваются следующие геометрические умения:
1)
строить образы
фигур при данном преобразовании;
2)
видеть
соответственные точки на соответствующих при том же преобразовании фигурах;
3)
выделять
элементы, определяющие преобразование;
4)
строить соответственные
при заданном преобразовании точки на произвольно заданных фигурах;
5)
использовать
специфические свойства преобразований.
В результате изучения теоретического
материала по геометрическим преобразованиям, учащиеся академических лицеев
смогут строить образы фигур при симметрии, повороте, параллельном переносе,
гомотетии; видеть соответственные при указанном отображении точки на
соответственных при том же отображении фигурах; выделять элементы, определяющие
отображение: ось симметрии, центр поворота, угол поворота, направление
параллельного переноса и его расстояние, центр и коэффициент гомотетии; строить
соответственные при указанном отображении точки на произвольных фигурах.
Приведем примеры, когда решение,
основанное на свойствах геометрических преобразований, значительно проще.
Задача 2.1.1. Через центр
О параллелограмма ABCD проведена
прямая l, пересекающая стороны ВС и AD параллелограмма соответственно в
точках M и N. Докажите, что 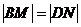 (рис.2.1.1)
(рис.2.1.1)
Решение (традиционное):
Отрезки BM и ND являются сторонами треугольников BMO и OND.
Чаще такие треугольники приходиться строить, что значительно осложняет
решение задачи. Мы выбрали простую задачу, чтобы показать сущность принципа.
Треугольники BMO и OND
подобны, т.к. BO=OD (свойство диагоналей
параллелограмма), 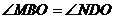 (накрест лежащие углы при параллельных
прямых),
(накрест лежащие углы при параллельных
прямых),  (вертикальные). Следовательно, BM=DN.
(вертикальные). Следовательно, BM=DN.
Решение (используя свойство
геометрических преобразований):
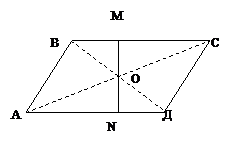
Точка О – центр симметрии
параллелограмма ABCD. Тогда Z0(B)=D, Z0(M)=N, т.к. N , следовательно, BM=DN.
, следовательно, BM=DN.
рис.2.1.1.
Задача 2.1.2.
Докажите, что прямая содержащая точку О пересечения диагоналей трапеции АВСД и
точку М- середину основания ВС, пересекает второе основание АД трапеции АВСД в
точке N, являющейся серединой основания АД
(рис2.1.2).
Решение (традиционное):
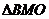 ~
~
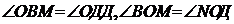 ,
следовательно,
,
следовательно, 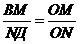 .
.
Аналогично, из подобия треугольников
МОС и АОN имеем: 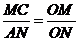 .
.
Значит, 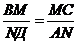 или
или
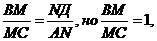 следовательно
следовательно 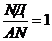 ,
т.е. AN=NД и N –
середина АД.
,
т.е. AN=NД и N –
середина АД.
Решение (используя свойство геометрических преобразований):
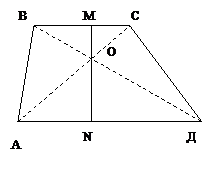 Рассмотрим гомотетию с центром О при
которой ВС
Рассмотрим гомотетию с центром О при
которой ВС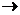 АД. Образ М/ точки М
принадлежит как отрезку АД ( М
АД. Образ М/ точки М
принадлежит как отрезку АД ( М ) так и прямой МО,
т.е. М/
) так и прямой МО,
т.е. М/  ,а потому М/=N. Так как гомотетия сохраняет отношение
,а потому М/=N. Так как гомотетия сохраняет отношение
расстояний, то  , т.е. N-– середина отрезка АД.
, т.е. N-– середина отрезка АД.
рис.2.1.2.
Задача 2.1.3. Впишите в данный острый
угол треугольник наименьшего периметра так, чтобы две его вершины принадлежали
сторонам угла, а третья – данной точке внутренней области угла (рис.2.1.3).
Решение данной задачи основано на
свойствах осевой симметрии. Строим точки М1 и М2,
симметричные данной точке М относительно прямых, содержащих стороны данного
угла. Точки пересечения отрезка М1М2 со сторонами угла
являются вершинами искомого треугольника. Периметр полученного треугольника
равен длине отрезка М1М2, периметр любого другого
треугольника, одной из вершин которого является точка М, а две другие
принадлежат сторонам данного угла равен длине ломанной, соединяющей точки М1
и М2.
Метод, основанный на признаках
равенства треугольников, в данном случае, является «беспомощным».
Задача 2.1.4. Впишите в
данный треугольник другой треугольник, стороны которого были бы параллельны
трем данным прямым.
Эффективным средством решения
данной задачи является метод гомотетии. Вначале следует построить треугольник
так, чтобы его стороны были параллельны данным прямым; две вершины принадлежали
сторонам данного треугольника так, чтобы все вершины оказались на сторонах
треугольника.
Таким образом, метод
геометрических преобразований позволяет решать большинство задач на
доказательство, построение и вычисление, упрощая при этом само решение.
В исследованиях психологов
Е.Н.Кабановой-Меллер [4], Н.А.Менчинской [5] и других делается вывод о том,
что знания сами по себе не превращаются в умения, для этого нужна специальная
работа. Поэтому, формированию умения использовать геометрические
преобразования при решении задач и доказательстве теорем, должно быть уделено
самое серьезное внимание. Для разработки методики формирования умения
необходимо выявить его компоненты, что позволит осуществить поэлементное
формирование этого умения.
Исходя
из теории поэтапного формирования умственных действий, мы сделали выводы о
преобразовании действия в умение, а затем и в навык, согласно которым, компонентами развития геометрических умений и навыков являются
следующие этапы:
1. Необходимо
разбить геометрические действия на операции, которые соответствуют
геометрическим знаниям, умения и навыкам учащихся академических лицеев, и
выделить ориентировочную основу для того, чтобы учащийся сам мог повторить
данное действие с новым материалом.
2. Опираясь на
ориентировочную основу, учащийся академического лицея выполняет действие. Для
этого необходимо развернуть (показать все операции и их взаимосвязь) и обобщить
(выделить из многообразия свойств объекта только те, которые необходимы для
выполнения действия) данное действие.
3. Моделирование выделенных свойств в
графической или буквенной формах. Перенесение
действий в задачную ситуацию.
4. Перенос
действия и свободное использование данного геометрического действия (умения) в
другие, более обобщенные ситуации.
5. Формирование
умственного действия, которое предшествует навыкам.
Компоненты умения в
использовании метода геометрических преобразований могут быть выявлены путем
анализа решения конкретных задач. В процессе этого анализа выявляются
элементарные умения, которые и являются компонентами учебных умений
использовать геометрические преобразования при решении задач.
Рассмотрим ещё ряд примеров[6].
I.
Задачи, решаемые методом осевой симметрии.
Задача 2.1.5. Даны
две окружности и прямая l.
Постройте равносторонний треугольник так, чтобы две его вершины принадлежали
данным окружностям, а одна из высот – прямой l .
Решение.
Предположим, что треугольник АВС искомый (рис. 2.1.4). Так как высота АД
равностороннего треугольника АВС принадлежит прямой l, то точки В и С симметричны относительно этой прямой
и лежат на данных окружностях (развивается умение строить на
произвольных окружностях точки, симметричные относительно данной прямой).
Если точка С принадлежит окружности F2 и
симметрична точке В, принадлежащей окружности F1, относительно прямой l, то точка С принадлежит также и образу окружности F1 при симметрии относительно l. Следовательно, точка С - общая для F2 и F1/ при симметрии S(l). Построив
окружность F1/, являющуюся образом окружности F1, найдём точку С. (развивается умение строить образ
окружности при осевой симметрии).
Затем строим точку В как
образ точки С при симметрии S(l), учитывая, что С принадлежит окружности F1/, и F1
симметрична F1/ (умение строить симметричные точки
на заданных симметричных окружностях). Последовательность операций,
выполняемых при решении этой задачи такова:
а) строим образ окружности F1 при симметрии S(l);
б) находим точки пересечения
окружностей F1/ и F2;
в) отыскиваем на окружности F1 прообразы точек пересечения окружностей F1/ и F2;
г) строим равносторонний треугольник
АВС ( А ).
).
Задача может иметь:
а) единственное решение, когда F2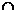 F1/=С
F1/=С
б) два решения, когда F2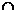 F1/={M,K}
F1/={M,K}
в) бесконечное множество решений,
когда F1/= F2.
Задача не имеет решений, когда F2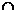 F1/=ǿ.
F1/=ǿ.
Итак, чтобы решить задачу
учащиеся должны владеть следующими умениями:
2) выделять соответственные при
осевой симметрии точки на соответственных при той же симметрии окружностях;
3) строить симметричные относительно
прямой точки на произвольных окружностях.
Задача 2.1.6. Окружность
F1 пересекает концентрические окружности F2 и F3 соответственно в точках А, В и С, Д.
Докажите, что хорды АВ и СД параллельны.
Решение. Пусть О-центр
окружности F1 и О1- центр окружности F1 и F2. И пусть F1 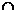 F2={A,B} F1
F2={A,B} F1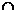 F3={C,D}.
F3={C,D}.
Тогда (ОО1) – ось
симметрии фигуры F=F1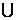 F2
F2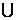 F3 (умение «видеть» ось симметрии).
F3 (умение «видеть» ось симметрии).
Так как А F1
F1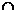 F2, а
F2, а 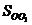 (А)
(А) F1
F1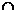 F2, т.е.
F2, т.е. 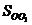 (А)=В (умение
видеть соответственные точки на соответственных фигурах).
(А)=В (умение
видеть соответственные точки на соответственных фигурах).
Аналогично, 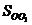 (С)=Д. Т.к. [AB]
(С)=Д. Т.к. [AB]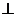 [ОО1] и [CD]
[ОО1] и [CD] 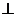 ОО1,
то АВ
ОО1,
то АВ 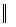 СД.
СД.
Анализируя решения этих и
других задач, решаемых методом осевой симметрии, приходим к выводу, что
овладение этим методом позволяет формировать и развивать следующие
геометрические умения и навыки:
1) строить образы фигур при осевой
симметрии;
2) «видеть» симметричные относительно
прямой точки на симметричных относительно этой же прямой фигурах;
3) строить ось симметрии;
1) находить симметричные относительно
прямой точки на произвольных заданных фигурах.
II. Задачи, решаемые методом поворота.
Задача 2.1.7. Постройте
равносторонний треугольник так, чтобы одной его вершиной была точка Р, друга
принадлежала прямой а, третья – прямой в.
Решение. Пусть 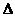 РКL искомый (рис.2.1.5). Тогда точки K и L
находятся на равном расстоянии от точки Р, принадлежат прямым а и в
соответственно и «видны» из точки Р под углом 600 (их
построение обеспечивается
РКL искомый (рис.2.1.5). Тогда точки K и L
находятся на равном расстоянии от точки Р, принадлежат прямым а и в
соответственно и «видны» из точки Р под углом 600 (их
построение обеспечивается
умением выделять на
заданных фигурах соответственные при данном повороте точки).
Т.к. точка L является образом точки К при
повороте вокруг точки Р на 600, то она принадлежит образу прямой а
при указанном повороте (умение строить образы фигур при повороте), т.е.
точка L
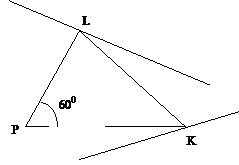 рис.2.1.5 есть общая точка прямой а/=RР
рис.2.1.5 есть общая точка прямой а/=RР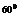 ( а) и
( а) и
прямой в.
Точка К является прообразом
точки L. Если в= RР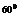 ( а), то задача имеет
бесконечное множество решений.
( а), то задача имеет
бесконечное множество решений.
В остальных случаях задача не
имеет более двух решений, т.к. прямая в имеет не более одной точки
пересечения с прямой а/ и не более одной точки пересечения с
прямой а//= RР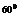 ( а).
( а).
 Задача 2.1.8. Через центр О треугольника АВС проведены две
прямые, образующие между собой угол в 600. Докажите, что отрезки
этих прямых, заключенные внутри треугольника, конгруэнтны (рис.2.1.6).
Задача 2.1.8. Через центр О треугольника АВС проведены две
прямые, образующие между собой угол в 600. Докажите, что отрезки
этих прямых, заключенные внутри треугольника, конгруэнтны (рис.2.1.6).
Решение:
Для доказательства конгруэнтности отрезков мы должны найти перемещение, при
котором один из отрезков отображается на другой. Так как угол между прямыми,
подмножествами
рис.2.1.6 которых являются указанные отрезки,
равен 600, то естественно
рассмотреть поворот вокруг точки О. Учитывая, что поворот вокруг точки О на
1200 отображает треугольник на себя, приходим к целесообразности
рассмотрения поворота вокруг точки О на 1200. При этом А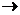 В, В
В, В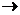 С, С
С, С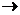 А, АВ
А, АВ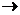 ВС,
ВС
ВС,
ВС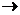 СА, СА
СА, СА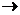 АВ.
АВ.
Точка Е  АС
отобразится на точку М.. Точка F
АС
отобразится на точку М.. Точка F  АВ – на N
АВ – на N  ВС. (
ВС. (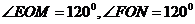 поворот
сохраняет пересечение фигур). Следовательно, FE
поворот
сохраняет пересечение фигур). Следовательно, FE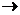 NM.
NM.
Значит, FE=NM.
Итак, мы видим, что овладение
этим методом требует формирование таких умений:
1) строить образы фигур при повороте;
2) находить соответственные при
повороте точки на соответственных при этом же повороте фигурах;
3) «видеть» центр поворота;
4) строить на соответственные при
повороте точки на произвольно данных фигурах.
III. Задачи, решаемые методом параллельного переноса.
Задача 2.1.9. Даны две окружности F1, F2 и прямая l. Проведите прямую, параллельную прямой l , на которой окружности F1 и F2 высекают конгруэнтные хорды.
 Решение: Пусть прямая l/ искомая, т.е. прямая l/ высекает на данных окружностях
конгруэнтные хорды АВ и А/В/ (рис.2.1.7). Тогда точки А
и А/, В и В/ можно рассматривать как соответственные при
параллельном переносе: О1
Решение: Пусть прямая l/ искомая, т.е. прямая l/ высекает на данных окружностях
конгруэнтные хорды АВ и А/В/ (рис.2.1.7). Тогда точки А
и А/, В и В/ можно рассматривать как соответственные при
параллельном переносе: О1 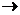 О1/
(умение строить соответственные точки на любых заданных фигурах).
О1/
(умение строить соответственные точки на любых заданных фигурах).
Т.к. точка А/ является образом
точки
А, принадлежащей
окружности F1, то точка
А/
принадлежит образу окружности F1.
Следовательно,
А/-
рис.2.1.7. общая точка окружности F2 и образа окружности F1 при параллельном переносе  (умение
строить образы фигур при параллельном переносе).
(умение
строить образы фигур при параллельном переносе).
Построив точку А/,
находим на окружности F1 её прообраз (умение выделять
соответственные при повороте точки на соответственных при том же повороте
фигурах).
Если F2= (F1), то задача имеет бесконечное множество решений. В остальных
случаях задача имеет не более четырех решений, т.к. окружность F2 имеет не более двух точек пересечения с окружностью F1/=
(F1), то задача имеет бесконечное множество решений. В остальных
случаях задача имеет не более четырех решений, т.к. окружность F2 имеет не более двух точек пересечения с окружностью F1/= (F1) и не более двух точек пересечения с окружностью F1//=
(F1) и не более двух точек пересечения с окружностью F1//= (F1).
(F1).
Задача 2.1.10. Расстояние между
центрами двух пересекающихся окружностей равных радиусов равно d.
Прямая, параллельная линии
центров, пересекает первую окружность в точках А и В, вторую – в точках С и Д.
Найдите длину отрезка АС (рис.2.1.8).
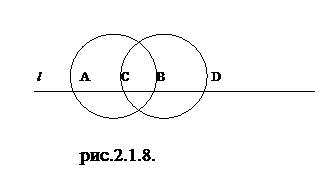 Решение. Обозначим центры данных
окружностей через О1и О2.
Решение. Обозначим центры данных
окружностей через О1и О2.
Тогда параллельный перенос 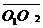 (умение выделять элементы,
(умение выделять элементы,
определяющие параллельный перенос) отобразит окружность с центром О1
на окружность с центром О2.(умение строить образы фигур при
параллельном переносе). Точка А при этом переносе перейдёт в точку С, а
точка В – в точку Д (умение видеть соответственные пи параллельном переносе
точки на соответственные при том же переносе фигурах).
Следовательно, АС=ВД= О1О2=d.
Нетрудно видеть, что при
овладении методом параллельного переноса требует формирования таких же умений,
как и при методах симметрии и поворота.
Задачи, решаемые методом гомотетии.
Задача 2.1.11. Дан угол АВС и
внутри него точка М. Проведите через точку М прямую так, чтобы отрезок её,
заключенный внутри угла АС, делится точкой М в отношении  .
.
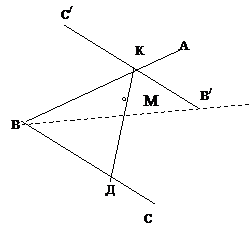 Решение: Пусть отрезок КД искомый,
т.е.
Решение: Пусть отрезок КД искомый,
т.е.  (рис.2.1.9). Тогда гомотетия Н
(рис.2.1.9). Тогда гомотетия Н отобразит точку Д на точку К (умение
выделять элементы, определяющие гомотетию).
отобразит точку Д на точку К (умение
выделять элементы, определяющие гомотетию).
рис.2.1.9
Т.к. Д ВС,
то К
ВС,
то К В/С/,
где В/С/ =Н
В/С/,
где В/С/ =Н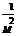 (ВС) (умение строить образы фигур
при гомотетии и «видеть» соответственные при гомотетии точки на соответственных
фигурах).
(ВС) (умение строить образы фигур
при гомотетии и «видеть» соответственные при гомотетии точки на соответственных
фигурах).
Следовательно, К=ВА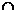 В/С/. Построив
точку К/ , найдем на ВС точку Д, являющуюся прообразом точки К при
гомотетии Н
В/С/. Построив
точку К/ , найдем на ВС точку Д, являющуюся прообразом точки К при
гомотетии Н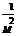 .
.
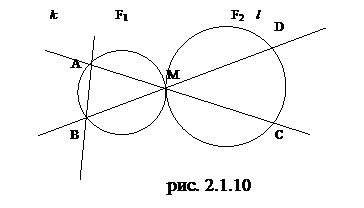
Задача 2.1.12. Через точку М
касания окружностей F1 и F2 проведены секущие k и l , пересекающие окружность F1, кроме точки М, в точках А и В, а окружность F2- точках С и Д. Докажите, что прямые АВ и СД
параллельны.
 Решение. Две окружности, касающиеся в точке М,
гомотетичны относительно этой точки (умение выделять центр гомотетии).
Рассмотрим гомотетию, при которой
Решение. Две окружности, касающиеся в точке М,
гомотетичны относительно этой точки (умение выделять центр гомотетии).
Рассмотрим гомотетию, при которой 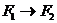 (умение видеть
образ данной фигуры).
(умение видеть
образ данной фигуры).
Эта
гомотетия отобразит точку А на точку С (рис2.1.10), а точку В на точку Д (умение
видеть соответственные фигуры при гомотетии точки на соответственных при той же
гомотетии фигурах).
Используя свойства гомотетии,
получаем АВ .
.
Таким образом, овладение методом
гомотетии требует формирование следующих геометрических умений учащихся
академических лицеев:
1) строить образы фигур при
гомотетии;
2) находить соответственные при
гомотетии точки на соответственных при той же гомотетии фигурах;
3) выделять элементы, определяющие
гомотетию (центр гомотетии, коэффициент);
4) строить соответственные при
заданной гомотетии точки на произвольных фигурах.
Анализ решения задач методами
симметрии, поворота, параллельного переноса и гомотетии позволили нам выделить
те умения, овладения которыми будут способствовать развитию у них таких
умений и навыков как: осмысленно подходить к поставленной проблеме; правильно
изображать пространственные фигуры на чертежах; комбинированного применения тех
или иных теорем и правил; распознавания различных геометрических объектов и их
свойств; решения задач повышенной трудности с применением различного типа
преобразований и групп преобразований; умение на практике применять полученные
теоретические формулы и преобразования; конструктивные умения.
Рассмотрим разработку
урока геометрии в академическом лицее.
Тема: « Движения ».
Цели урока.
Развивающая цель –
формирование и развитие умений использования метода геометрических
преобразований в решении задач.
Воспитательная цель -
развитие умения использования методов научного исследования в решении задач.
Оборудование. Таблица по
теме «движения», компьютерная программа – тест для проверки знаний и умений по
теме, линейки и карандаши, карточки-образцы решенных задач.
Примерный план
1. Организационный момент.
2. Проверка домашнего задания и проверка
знаний и умений, приобретенных ранее по данной теме (тест – опрос на
компьютере).
3. Ввести понятие отображения
пространства на себя: если каждой точке М пространства сопоставлена в
соответствии некоторая точка М1, причём любая точка М1
пространства оказалась поставленной в соответствие какой-то точке М, то
говорят, что задано отображение пространства на себя.
4. Отметить, что особую роль в геометрии
играют отображения пространства на себя, сохраняющие расстояние между точками.
Они называются движениями пространства.
Таким образом, если при
движении пространства точки А и В переходят (отображаются) а точки А1
и В1, то АВ=А1В1. В учебнике рассматриваются
четыре вида движений и доказывается, что центральная симметрия и параллельный
перенос являются движениями.
Доказательства
этих утверждений достаточно прозрачны, они могут быть изучены на одном уроке.
В
случае центральной, осевой и зеркальной симметрий используется метод координат
сначала устанавливается связь между координатами двух симметричных точек М
(х,у,z) и М1(х 1,у1
,z1).
Например,
если рассматривается центральная симметрия относительно начала координат, то х1
= -х, у1 = -у, z1= -z. Далее для любых двух точек А(х 1,у1 ,z1) и В (х2, у2, z2 )и симметричных им точек А1 и
В1 доказывается, что АВ=А1В1,то есть
сохраняется расстояние между точками.
Доказательство
утверждения о том, что параллельный перенос является движением, можно привести
с помощью векторов.
5. Решение задач.
Задача
2.2.3. Докажите, что при центральной симметрии прямая не проходящая через
центр симметрии, отображается на параллельную ей прямую.
Решение.
а) Рассмотрим центральную симметрию пространства с центром О и произвольную
прямую АВ, не проходящую через точку О
Прямая АВ и точка О
определяют единственную плоскость α. Точки А и В переходят при данной
симметрии в точки А1 и В1, также лежащие в плоскости
α. Поэтому и вся прямая А1В1 лежит в плоскости
α.
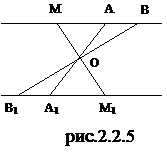
б) Докажем сначала, что прямые ОАВ и
ОА1В1 равны по двум сторонам (ОА=ОА1, ОВ=ОВ1)
и углу между ними ( АОВ =
АОВ = А1ОВ1).
Из равенства треугольников следует, что
А1ОВ1).
Из равенства треугольников следует, что  АОВ =
АОВ = А1В1О, т.е. равны
накрест лежащие углы при пересечении прямых АВ и А1В1
секущей ВВ1. следовательно, АВ║А1В1
А1В1О, т.е. равны
накрест лежащие углы при пересечении прямых АВ и А1В1
секущей ВВ1. следовательно, АВ║А1В1
в) Докажем теперь, что при
центральной симметрии с центром О прямая АВ отображается на прямую А1В1
, то есть произвольная точка М прямой АВ переходит в некоторую точку М1
прямой А1В1 ( иначе говоря, произвольная точка М прямой
АВ симметрична некоторой точке М1 прямой А1В1
относительно точки О), и обратно, произвольная точка М1 прямой А1В1
симметрична относительно О некоторой точке М прямой АВ. Возьмём на прямой АВ
произвольную точку М (отличную от А) и проведём прямую МО. Она пересекает
прямую А1В1 в какой-то точке М1. (см. рис
2.2.7) Треугольники МАО и М1А1О равны по стороне (АО=А1О)
и прилежащие к ней углы ( МОА=
МОА= М1 ОА1 , как
вертикальные;
М1 ОА1 , как
вертикальные;  МАО=
МАО= М1
ОА1, как накрест лежащие при пересечении параллельных прямых АВ и А1В1
секущей ММ1). Поэтому МО=ОМ1, а это и означает, что точка
М переходит при симметрии относительно О в точку М1, лежащую на
прямой А1В1. Аналогично доказывается обратное: любая
точка М1 прямой А1В1 симметрична некоторой
точке М прямой АВ относительно О.
М1
ОА1, как накрест лежащие при пересечении параллельных прямых АВ и А1В1
секущей ММ1). Поэтому МО=ОМ1, а это и означает, что точка
М переходит при симметрии относительно О в точку М1, лежащую на
прямой А1В1. Аналогично доказывается обратное: любая
точка М1 прямой А1В1 симметрична некоторой
точке М прямой АВ относительно О.
Итак, при симметрии с
центром О прямая АВ, не проходящая через точку О, отображается на параллельную
прямую А1В1 .
Задача 2.2.4. Докажите,
что при центральной симметрии плоскость, не проходящая через центр симметрии,
отображается на параллельную ей плоскость.
Решение. Рассмотрим
центральную симметрию пространства с центром в точке О и произвольную плоскость
α., не проходящую через точку О. (рис.2.2.6). Пусть прямые а и в,
пересекающиеся в точке А, лежат в плоскости α.. При симметрии с центром в
точке О прямые а и в переходят в соответственно параллельные
прямые а1 и в1 .
При этом точка А переходит в
некоторую точку А1, лежащую на прямой в а1 , так
и на прямой в1, а значит прямые а1 и в1
пересекаются.
Пересекающиеся прямые а1
и в1 определяют единственную
плоскость α.1. По
признаку параллельности плоскостей α.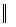 α.1.
в1 а1
α.1.
в1 а1

Далее не трудно доказать, что
при центральной симметрии с центром в точке О плоскость α.
отображается на плоскость α.1. Доказательство можно провести
аналогично тому, как было сделано в предыдущей задаче, как для прямых АВ и А1В1.
6. Постановка домашнего задания (по
карточкам с решениями задач).
Задача 2.2.5. При
зеркальной симметрии относительно плоскости α. плоскость β
отображается на плоскость β1. Докажите, что если β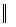 α, то β1
α, то β1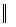 α..
α..
Решение. Доказательство
проведём методом от противного. Предположим, что β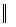 α,
а плоскости α.1 и β1 пересекаются. Тогда они имеют
общую точку М. Так как М
α,
а плоскости α.1 и β1 пересекаются. Тогда они имеют
общую точку М. Так как М α, то при данной
зеркальной симметрии точка М отображается в себя. Отсюда следует, что точка М,
которая принадлежит плоскости β1 , лежит также в плоскости
β. Но тогда α. и β пересекаются. Полученное противоречие
показывает, что наше предположение ложно, следовательно, β1
α, то при данной
зеркальной симметрии точка М отображается в себя. Отсюда следует, что точка М,
которая принадлежит плоскости β1 , лежит также в плоскости
β. Но тогда α. и β пересекаются. Полученное противоречие
показывает, что наше предположение ложно, следовательно, β1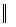 α..
α..
Задача 2.2.6. Докажите,
что центральная симметричность цилиндра равносильна центральной симметричности
его основания.( цилиндр общего вида)
Решение. Пусть Z-цилиндр, имеющий центр симметрии –
точку О, а Q и Q′ - его основания. Пусть Q лежит в плоскости α, а Q′ - в плоскости α′ . Проведем через О
прямую, параллельную образующим цилиндра. Она пересечёт плоскость α в
точке А, а плоскость α ′ в точке А′. Точка О является
серединой отрезка АА′ (так как О- центр симметрии цилиндра). Покажем, что
А – центр симметрии основания Q, а
точка А′ - основания Q′
(рис.2.2.9).

Возьмём любую точку х Q, и пусть У′ - симметричная ей точка (относительно О).
ясно, что У′
Q, и пусть У′ - симметричная ей точка (относительно О).
ясно, что У′  Q′. Точка У′ является одной из концов образующей
УУ′ цилиндра Z. Так как ХО=
У′О и ОА
Q′. Точка У′ является одной из концов образующей
УУ′ цилиндра Z. Так как ХО=
У′О и ОА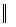 УУ′, то ХА=АУ. Поэтому
точка У симметрична точке Х относительно точки А.
УУ′, то ХА=АУ. Поэтому
точка У симметрична точке Х относительно точки А.
Итак, А - центр симметрии
основания Q. Точно так же А′ - центр
основания Q′.
Пусть теперь, наоборот, дано,
что Z имеет основание, симметричное
относительно некоторой точки А. Тогда строим образующую АА′ и берём точку
О - середину этого отрезка. Возьмём затем любую точку М Z и проведём через неё образующую
ХХ′. Точка У, симметричная точке Х относительно точки А, будет точкой
основания Q. Идущая из У образующая УУ′
цилиндра Z пересечет прямую ОМ в точке М′
Z и проведём через неё образующую
ХХ′. Точка У, симметричная точке Х относительно точки А, будет точкой
основания Q. Идущая из У образующая УУ′
цилиндра Z пересечет прямую ОМ в точке М′ Z, симметричной точке М относительно точки О. Итак, О- центр
симметрии цилиндра Z.
Z, симметричной точке М относительно точки О. Итак, О- центр
симметрии цилиндра Z.
Задача 2.2.7. Куб
повернули на 600 относительно его диагонали. Найдите пересечение и
объединение исходного и полученного куба.
Решение. Известно, что в
кубе есть сечение, являющееся правильным шестиугольником и
перпендикулярное диагонали куба. Если в кубе
АВСДА1В1С1Д1 (рис.2.2.8)

взять диагональ АС
1,
то такое сечение можно получить, если провести через середину этой диагонали
точку О- плоскость α
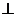
АС
1. В
сечении получим правильный шестиугольник KLMNPQ=T,
причём K- середина ребра ДД1 и
т.д.
При повороте куба вокруг АС1 на 600
рис
2.2.8 шестиугольник Т перейдёт сам в себя. Будем считать, что
точка К перешла в точку L,
точка L- в точку М и т.д. Так как вершины А
и С1 лежат на оси поворота, то 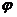 (А)=А
и
(А)=А
и 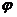 (С1)=С1.
(С1)=С1.
Поэтому отрезки АК,AL,AQ и т.д. перейдут в отрезки AL,AM,AK и т.д. Поскольку отрезки AK и AL лежат в грани АА1Д1Д, то плоскость
этой грани после поворота 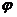 перейдёт в
плоскость ALM, а образ этой грани квадрат
перейдёт в
плоскость ALM, а образ этой грани квадрат 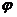 (АА1Д1Д)- отсечёт
от куба тетраэдр AA1LM. Кроме того, от куба АВ…С1Д1
повёрнутый куб отсечёт ещё два тетраэдра с вершиной А – ABNP и AДQK, а также три
тетраэдра с вершиной С1. Следовательно, искомая часть кубов состоит
из двух шестиугольных пирамид с вершинами А и С1 и общим основанием KLMNPQ.
(АА1Д1Д)- отсечёт
от куба тетраэдр AA1LM. Кроме того, от куба АВ…С1Д1
повёрнутый куб отсечёт ещё два тетраэдра с вершиной А – ABNP и AДQK, а также три
тетраэдра с вершиной С1. Следовательно, искомая часть кубов состоит
из двух шестиугольных пирамид с вершинами А и С1 и общим основанием KLMNPQ.
 Далее предложим задачи, в решении которых используются геометрические
преобразования.
Далее предложим задачи, в решении которых используются геометрические
преобразования.
Задача 2.2.8. В трапеции АВСД с основаниями ВС и АД на сторонах АВ и СД выбраны
точки К и М. Докажите, что если  ВАМ =
ВАМ =  СДК, то
СДК, то  ВМА=
ВМА= СКД.
СКД.
Решение. Пусть О - точка
Пересечения продолжений боковых
сторон
АВ и СД данной трапеции.
Выполним последовательно
симметрию S относительно
рис 2.2.9
. биссектрисы  АОД
и гомотетию Н
АОД
и гомотетию Н
с центром О и
коэффициентом ОД /
ОА. При этом точка А перейдёт в Д,
а точка В – в точку С (поскольку ОС / ОВ = ОД / ОА) (рис.2.2.9),  ОАМ – в равный ему по условию
ОАМ – в равный ему по условию  ОДК. Следовательно, точка М, лежащая на
пересечении прямых АМ и ОД, перейдёт в точку пресечения образов этих прямых –
ДК и ОА, т.е. в точку К. Итак, точки А,М,В переходят, соответственно, в Д,К,С,
а значит,
ОДК. Следовательно, точка М, лежащая на
пересечении прямых АМ и ОД, перейдёт в точку пресечения образов этих прямых –
ДК и ОА, т.е. в точку К. Итак, точки А,М,В переходят, соответственно, в Д,К,С,
а значит,  АМВ =
АМВ =  ДКС.
ДКС.
Задача 2.2.9. Пусть АД – высота
в прямоугольном треугольнике АВС,  А=900.
Прямая, проходящая через центр окружностей, вписанных в треугольники АВД и АСД,
пересекает стороны АВ и АС соответственно в точках К и L. Докажите неравенство SАВС
А=900.
Прямая, проходящая через центр окружностей, вписанных в треугольники АВД и АСД,
пересекает стороны АВ и АС соответственно в точках К и L. Докажите неравенство SАВС 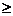 2SАКL (рис.2.2.10)
2SАКL (рис.2.2.10)
Решение. Докажем, что
AK = AL = АД. Выполним последовательно
поворот
вокруг точки Д на угол 450 и гомотетию с центром Д и
коэффициентом
ДО1 / ДВ.
( ВДО1 =
ВДО1 =  АДО2= 450, а ДО2
/ ДА= ДО1 / ДВ,
АДО2= 450, а ДО2
/ ДА= ДО1 / ДВ,
так как треугольники ДАС и
ДВА подобны).
Следовательно, угол между прямыми ВА и
О1О2 равен 450, т.е.  LKA=450.
А значит
LKA=450.
А значит
KAL – прямоугольный равнобедренный.
Рис.2.2.10
Треугольники
АО1К и АО1 Д равны: они имеют общую сторону АО1
и равные углы ( АКО1 =
АКО1 =
 АДО1
= 450, АО1 – биссектриса угла КАД). Поэтому AL = AK = АД.
АДО1
= 450, АО1 – биссектриса угла КАД). Поэтому AL = AK = АД.
Пусть  АВС =
АВС = 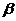 ,
тогда АВ=
,
тогда АВ= , AC=
, AC= и
и
SАВС = 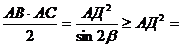 2
SAKL.
2
SAKL.
При sin2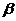 =1, т.е. для (
=1, т.е. для (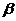 =450) равнобедренного
треугольника АВС достигается равенство.
=450) равнобедренного
треугольника АВС достигается равенство.
Задача 2.2.10. Из вершины
А квадрата АВСД внутрь квадрата проведены два луча, на которые опущены
перпендикуляры BK,BL, ДМ, ДN из вершин В и Д. Докажите, что отрезки KL и MN равны и перпендикулярны.
Решение. Рассмотрим поворот R вокруг центра квадрата на 900,
при котором точки В и А перейдут соответственно в А и Д. Покажем, что при
этом повороте отрезок KL
перейдёт в MN. Поскольку  КВА=
(900-
КВА=
(900-  КАВ)=
КАВ)=  КАД
и аналогично
КАД
и аналогично  КАВ =
КАВ =  АДМ,
луч ВК при этом перейдёт в луч АМ, а луч АК - в луч ДМ..
АДМ,
луч ВК при этом перейдёт в луч АМ, а луч АК - в луч ДМ..
Как на рисунке 2.2.11

рис.2.2.11.
Следовательно, точка К перейдёт
в точку М, т.е. R (K) = M. Аналогично
R (L) = N
В результате решения этих задач,
(здесь речь идет о задачах в условии которых не фигурируют геометрические
преобразования) у учащихся развиваются умение применять геометрические
преобразования, как метод решения задач.
7. Подведение итогов
урока.
При подготовке к урокам, нами были
проанализированы системы упражнений, развивающие определённые геометрические
умения и навыки, составленные исследователями-методистами. Например, системы
упражнений по планиметрии, предложенная С.М. Саврасовой (Журнал «Математика в
школе» № 6 1987 г., стр 28.) . Автор развил систему упражнений на 4 серии,
каждая серия состоит из трех частей:
1) справочная таблица;
2) набор тренировочных упражнений;
3) проверочная работа.
Серии были сделаны тематически:
1. Метрические соотношения в подобных
треугольниках.
2. Соотношения между углами и сторонами
в прямоугольном треугольнике.
3. Площади фигур.
4. Правильные многоугольники.
Для этих тем были сделаны справочные
таблицы, учащимся предъявляются готовые рисунки и таблицы с тренировочными упражнениями
и их решениями.
Предлагаемая таким образом
система, направлена на ликвидацию недостатков в знаниях по планиметрии
учащихся старших классов и на формирование специальных математических навыков
решения задач планиметрии.
В системе задач на
вычисление, предложенной Б.А. Абремским [7] геометрические задачи на
вычисление подразделены следующим образом:
- выявление зависимости между
элементами некоторой фигуры;
- непосредственное отыскание искомого
из соотношения, содержащего одно неизвестное;
- выделение вспомогательной задачи;
- операция, посредством которой
некоторые неизвестные выражаются через переменную или переменные;
- составление уравнения или системы
уравнений;
- вычленение в геометрической
ситуации несколько взаимно исключающих друг – друга случаев.
Система задач В.А.
Онищук[11] составлена в соответствии с дидактическим назначением:
-актуализации опорных знаний
(подготовительные);
-усвоения знаний (вводные);
-первичного применения знаний (пробные);
-овладения навыками в стандартных
условиях (тренировочные);
- творческого переноса знаний и навыков (творческие);
-контроля, коррекции и оценки навыков
и умений (контрольные).
Близкой к системе В.А.
Онищук является система, предложенная В.А. Гусевым [8], связанная с овладением
учащимися приемами «синтез» и «анализ»:
-задачи и вопросы, ответы на которые
учат делать выводы («учись делать выводы»);
-задачи для самоконтроля («ищи
причину вывода»): решая их, нужно не только получать следствие из условия
задачи, но и выяснить причину появления этого следствия;
-стандартные задачи – наиболее
простые задачи; без умения их решать нельзя получить положительную оценку;
-учебные задачи – самая
многочисленная группа задач, которые придется решать в аудитории и дома. Эти
задачи позволяют усвоить новый теоретический материал и перейти к решению более
сложных задач;
-творческие задачи; к ним относятся
задачи, которые не удается решить стандартными методами; для их решения нужно
выдвинуть некоторую новую идею;
-исследовательские задания. Для
своего решения они требуют значительных усилий. Такие задания не могут
полностью решаться в аудитории, они предполагают работу дома, возможно, даже не
одного, а нескольких студентов.
В предложенных системах
не проведена дифференциация уровней развития умений и навыков. Поэтому,
проанализировав ряд подобных систем, для дальнейшего развития геометрических
умений и навыков учащихся академических лицеев мы предлагаем классифицировать
систему задач с применением геометрических преобразований следующим образом.
1. Систему задач разбиваем на 5 уровней
сложности. Степень трудности задач этих уровней определяется набором
используемых элементов знаний:
Первый уровень - воспроизводящий; задачи, составляющие его, предназначены для
восстановления формально-логической структуры ранее изученных простейших
понятий, образующих основу для формирования более сложных понятий.
Второй уровень - фактический; он соответствует начальному уровню формирования
сложных понятий, который заключается в накоплении знаний о способах
формально-логического описания простейших понятий, состоящего в основном из
фактов; отличается от первого уровня увеличением числа структурных единиц
понятий, необходимых для описания развернутого решения задачи.
Решения задач первого-второго уровней ограничиваются приведением единичных
фактов, основанных на основных характеристиках геометрических понятий и
операциях над ними.
Третий уровень - операционный; решение задач этого уровня заключается в умении
осуществлять и полно описывать простейшие логические операции по готовому
образцу, характеризуется образованием частносистемных ассоциаций и наличием
основных связей между понятиями.
Микросистемы задач первого - третьего уровней соответствуют минимально
необходимому качеству усвоения понятий, требуемого для освоения базового курса,
умение восстанавливать развернутое решение задач этих уровней отражает степень
сформированности основных понятий и способов деятельности.
Четвертый уровень - аналитико-синтетический; его задачи требуют умения
обобщать, дифференцировать простейшие и сложные понятия, выделять главные идеи,
основные положения, вскрывать разнообразные связи между понятиями, проводить
аналогии, формировать полную структуру решения задачи посредством выделения ранее
применяемых понятий и описания связей между ними.
Пятый уровень - творческий; он требует обобщений и переноса знаний в новые
ситуации, создания нестандартных алгоритмов познавательных и практических
действий.
2. Система задач, определенная для каждого тематического занятия,
открыта для предварительной самостоятельной работы учащихся.
3. Требование открытости, а значит и
предварительной работы учащихся с каждой из задач системы, обеспечивает
возможность оценки уровня развития геометрических умений и навыков.
Дидактическая характеристика уровня системы задач полно характеризует
качественный уровень овладения учащимся умениями и навыками.
4. Переход к решению задачи следующего уровня может осуществляться
только после положительного тестирования развернутого решения, содержащего
рассмотрение всех принципиально различных случаев организации данных, влияющих
на структуру решения.
5. Порядковый номер уровня системы задач может служить баллом для оценки
работы учащегося во время учебного занятия и оценки уровня развития
геометрических умений и навыков учащихся.
Как было отмечено выше, в
процессе выполнения упражнений по геометрии происходит совершенствование умений
и навыков измерения, построения, изображения, моделирования, конструирования,
приближённых вычислений, доказательства и необходимости аргументирования того
или иного действия. Система упражнений, предлагаемая нами, направлена на
комплексное развитие указанных геометрических умений и навыков. Кроме того,
система упражнений удовлетворяет требованиям системности, а также как указано
в [9] "… требованиям полноты и целостности, органической связи отдельных
видов упражнений, преемственности и перспективности, вариативности ".
Требование об открытости
заданий для самостоятельной работы учащихся, способствует развитию умений и
навыков самостоятельности, готовности учащихся к самообразованию.
Задача первого и второго
уровней системы упражнений направлены на развитие умений и навыков по формированию
нового понятия.
-
упражнения на
применение ранее изученных понятий и теорем;
-
упражнения
практического характера;
-
упражнения на
построения объектов, удовлетворяющих указанным свойствам;
-
упражнения с
моделями фигур;
-
упражнения на
распознавания объектов, принадлежащих объёму понятия;
-
упражнения на
выделение следствий из определения понятия;
-
упражнения на
дополнение условий (распознавание и выведение следствий);
-
упражнения на
составление родословной понятия;
-
упражнения на
применение понятия в различных ситуациях;
-
упражнения на
систематизацию понятий.
Задачи III-IV уровней системы упражнений включают в себя упражнения,
направленные на развитие умений и навыков доказательства теорем и задачи на
доказательства. Перечислим их:
-
упражнения на
измерение величин, на оперирование моделями фигур;
-
упражнения с
практическим содержанием;
-
упражнения на
применение ранее изученных теорем и понятий;
-
упражнения на
выделение условия и заключения теоремы;
-
упражнения на
распознавание ситуации, удовлетворяющих теореме;
-
упражнения на
ознакомление с методом доказательства теоремы;
-
упражнения,
моделирующие способ доказательства;
-
упражнения на
выделения в доказательстве недостающих утверждений и их обоснований;
-
упражнения на
систематизацию теорем;
-
упражнения на
составление родословной теоремы;
-
упражнения на
составление планов доказательства теоремы;
-
упражнения на
составление алгоритмов.
Покажем пример системы задач на геометрические преобразования плоскости и
пространства.
Поскольку важным элементом
математической культуры учащегося лицея является не только знание свойств
движений и преобразований, а умение применять их к доказательству теорем и
решению задач, необходимо показать методику решения задач с применением
определенных геометрических преобразований и их композиций.
Уровень 1.
Задача
2.2.11. На рисунке 2.2.12. изображен угол АВС. Постройте угол, симметричный
данному относительно оси 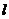 .
.
Задача
2.2.12. Докажите, что при движении вертикальные углы отобразятся на
вертикальные углы.
Задача
2.2.13. На рисунке 2.2.13 изображен угол АВС. Постройте угол, симметричный
данному углу относительно центра О.
Задача
2.2.14. Докажите, что при движении смежные углы отображаются на смежные углы.

рис.2.2.12. рис. 2.2.13.
Уровень 2.
Задача
2.2.15. Постройте произвольный треугольник и его образ при симметрии
относительно прямой, содержащей биссектрису одного из его внешних углов.
Задача
2.2.16. Докажите что при движении подобные ромбы отображаются на подобные
ромбы.
Задача
2.2.17. Постройте произвольный треугольник и его образ при симметрии
относительно точки пересечения его высот.
Задача
2.2.18. Докажите что при движении подобные прямоугольники отображаются на
подобные прямоугольники.
Уровень 3.
Задача
2.2.19. При помощи одной линейки постройте ось симметрии равнобедренной
трапеции.
Задача
2.2.20. При некотором движении отрезок АВ отображается на отрезок ЕР, АВ=12см.
Точка М принадлежит отрезку АВ, АМ=2 см. Точка М отображается на точку Н.
Найдите НЕ.
Задача
2.2.21. На рисунке 2.2.14. отрезки АВ и А1В1 центрально
симметричны относительно некоторого центра. С помощью одной линейки постройте
образ точки М при этой симметрии.
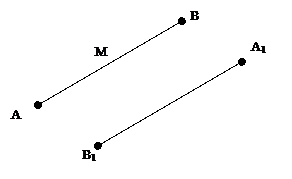
рис. 2.2.14
.
Задача
2.2.22. Точка К принадлежит отрезку МН и делит его в отношении 3:2, считая от
точки М. При некотором движении отрезок МН отображается на отрезок ЕР, а точка
К – на точку Т. Найдите отношение ЕТ:ТР.
Уровень 4.
Задача 2.2.23. На рисунке 2.2.15.
изображены две окружности и прямая 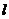 . Найдите на этих окружностях точки,
симметричные друг другу относительно прямой l.
. Найдите на этих окружностях точки,
симметричные друг другу относительно прямой l.
рис 2.2.15.
Задача 2.2.24.
Докажите, что равнобедренные трапеции АВСD и А1В1С1D1 (АВ и CD -основания) равны, если АВ= А1В1
, AD=A1D1 и угол ВАD= углу В1А1D1 .
Задача 2.2.25. На
рисунке 2.2.16. изображены прямые а и в и точка О. Найдите на этих прямых
точки, симметричные друг другу относительно центра О.
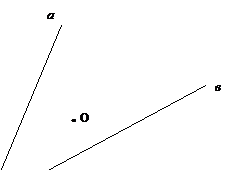
рис.
2.2.16.
Задача 2.2.26. Докажите, что два параллелограмма равны, если диагонали и угол между
ними одного параллелограмма равны диагоналям и углу между ними другого
параллелограмма.
Уровень5.
Примером задач пятого (творческого) уровня
могут служить следующие задачи:
Задача 2.2.27. Построить отрезок,
являющийся образом отрезка АВ при повороте вокруг точки О на угол – 700
Решение. Проведём луч ОА и
построим луч l,
получающийся из луча ОА поворотом на 700 (против часовой стрелки).
 На луче l построим
такую точку А1,
что
О А1 = ОА ( рис.4) П(А)= А1.
Аналогично
строим П (В) = В1.
На луче l построим
такую точку А1,
что
О А1 = ОА ( рис.4) П(А)= А1.
Аналогично
строим П (В) = В1.
Отрезок
А1
В1 является образом отрезка АВ.
Задача 2.2.28. На
сторонах треугольника АВС построены вне его равносторонние треугольники АВР,
АСН, ВСМ ( рис. 2.2.18.). Доказать, что отрезки АМ, ВН, СР равны.
Решение.
При повороте на 600 вокруг
точки
А имеем: П(Н)=С, П(В) =Р.
Следовательно,
отрезок АВ переходит в
отрезок
СР. Аналогично получаем, при повороте
на 600 вокруг точки В
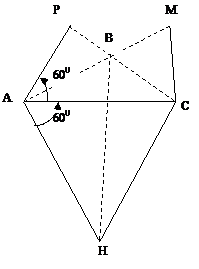
П(С)=М, П(Р)=А
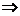
СР=АМ. Таким
образом,
АМ=ВН=СР.
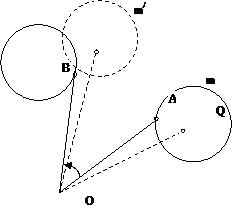
Задача 2.2.29. Даны две
окружности m,n и точка О. Найти на этих окружностях такие точки
А,В, что отрезки ОА, ОВ равны и составляют между собой угол
50
0 .
Но точка В лежит и на
окружности n. Значит, В - точка пересечения
окружностей m′ и n.
Проведённое рассуждение
делает понятным решение задачи. Построим окружность m′, получающуюся из m поворотом на 500 вокруг точки О. Для этого
нужно построить точку Q′,
получающуюся из центра Q
окружности m поворотом на 500 и
провести окружность того же радиуса с центром Q′. Затем обозначаем через В точку пересечения
окружностей m′ и n, а через А – точку, образом которой при этом повороте
является В. Точки А и В – искомые.
Поворот может
осуществляться на 500 , либо на - 500 , поэтому задача
может иметь до четырёх решений.
Задача 2.2.30. Даны
окружность S с центром О и точка А. Провести в
окружности хорду MN данной длины
так, чтобы из точки А она была видна под углом 400 .
Решение. Отбросим на время
требование о том , чтобы хорда MN
была видна из точки А под углом 400. Далее построим какую-нибудь
хорду НК, имеющую требуемую длину. Далее построим какую-нибудь точку Т, из
которой хорда НК видна под углом 400 (рис.2.2.20.)
Окружность, описанная вокруг
треугольника НКТ, обладает тем свойством, что из любой точки дуги НК
(содержащей точку Т) хорда НК видна под углом 400. Обозначим эту
дугу через а. Говорят, что дуга а «вмещает» угол 400.
Теперь ясно, что нужно повернуть эту дугу а вокруг точки О на такой
угол, чтобы повёрнутая дуга прошла через точку А.
Для того, чтобы определить,
на какой угол нужно осуществить поворот, проведем окружность q с центром О, проходящую через точку
А, и обозначим через точку пересечения этой окружности с дугой а (рис.2.2.21).
При повороте вокруг точки О на угол 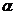 =
= ВОА
дуга а перейдет в дугу а1 проходящую через точку А, а
хорда НК перейдет в искомую хорду MN, которая видна из точки А под углом 400 . Окружность q пересекает дугу а в двух
точках В и В′. Поэтому задача имеет два решения.
ВОА
дуга а перейдет в дугу а1 проходящую через точку А, а
хорда НК перейдет в искомую хорду MN, которая видна из точки А под углом 400 . Окружность q пересекает дугу а в двух
точках В и В′. Поэтому задача имеет два решения.
Задача 2.2.31. На сторонах АС
и АВ треугольника АВС вне его построены параллелограммы ABLK и ACMN так, что АВ : AL = AC : AN = t,  BAL =
BAL =  ACM=
ACM=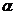 .
Выразите медиану AS треугольника
АВС через длину отрезка NL.
Найти угол между прямыми AS и NL.
.
Выразите медиану AS треугольника
АВС через длину отрезка NL.
Найти угол между прямыми AS и NL.
Решение. Пусть обход треугольника АВС происходит в положительном направлении
(рис.2.2.22.).Построим 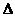 АВС до параллелограмма АВДС.
Рассмотрим преобразование состоящее из последовательного применения поворота на
угол (180-
АВС до параллелограмма АВДС.
Рассмотрим преобразование состоящее из последовательного применения поворота на
угол (180-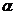 ) и гомотетии с центром в точке В и
коэффициентом
) и гомотетии с центром в точке В и
коэффициентом
1/ t (т.е. композицию двух преобразований).
При этом преобразовании П(А)=К, П(Д)=N1, т.е. П(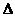 АВД)=
АВД)= 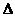 КВN1, подобный ему с коэффициентом 1/ t .
КВN1, подобный ему с коэффициентом 1/ t .
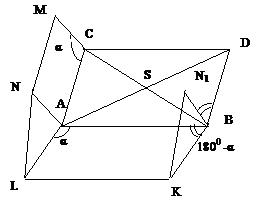
рис.2.2.22.
Легко
видеть, что 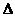 КВN1 получается из LAN параллельным переносом на
КВN1 получается из LAN параллельным переносом на 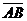 . Следовательно АS=
. Следовательно АS=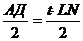 , угол между прямыми AS и LN равен
, угол между прямыми AS и LN равен 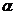 (или 1800-
(или 1800-
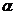 ).
).
ЛИТЕРАТУРА
1. Национальная программа по подготовке
кадров. - Т. 1997г.
2. Ўрта махсус касб-ҳунар таълимининг умумтаълим фанлари
давлат таълим стандартлари ва ўқув дастурлари.- Т.,2001г.- стр.20-23.
3. СаранцевГ.И. Сборник задач на
геометрические преобразования. Издание: второе, переработанное и
дополненное.- М.:Просвещение, 1981.-112с.
4. Кабанова-Меллер
Е.Н. Психология формирования знаний и навыков у школьников: Проблема
приемов умственной деятельности / Кабанова-Меллер Евгения Николаевна. - М.:
Академия пед. наук РСФСР, 1962. - 376 с.: ил.
5. Менчинская Н.А. Проблемы учения и
развития //Проблемы общей, возрастной и педагогической психологии. – М., 1978г.
6. СаранцевГ.И. Решаем задачи на
геометрические преобразования: Сборник задач по геометрии для организации
самостоятельной работы Изд. 3-е, перераб., доп.- М.:Просвещение, 1997.- 192с.
7. Абремский Б.А. //Ж. Математика в
школе № 6, Москва, 1990 год. - стр 37.
8. Гусев В.А., Орлов В.В., Панчищина
В.А. и др. Методика обучения геометрии: учеб. Пособие для студ. высш. учеб.
заведений. – М.: издательский центр «Академия». – 386 с
9. Султанова Х. Методика развития геометрических
умений и навыков учащихся академических лицеев. // Ж.
Узлуксиз таълим. – 2004. - № 6. – С. 57-65.
10. Султанова
Х., Жуманиёзов Қ. Роль
метода геометрических преобразований в развитии геометрических умений и
навыков академических лицеев.// Ж. Педагогик таълим. -2005.- № 1. – С. 34-35.
11. Урок в
современной школе. Онищук В.А. – М.: Просвещение, 1981. –191 с.