Анализ экономических задач оптимизации

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ

Государственное образовательное учреждение

высшего профессионального образования

РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТОГОВО-ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ

Волгоградский филиал

Кафедра высшей математики и информатики

Контрольная работа

по дисциплине: Информационные технологии в торговле

Исполнитель: студент 4 курса заочной формы обучения

факультета: «Экономика и управление на предприятии (торговли)»

Каплунова Ольга Александровна

Рецензент: Дмитриева Ирина Сергеевна

Волгоград 2008г.

СОДЕРЖАНИЕ

Задача №1 Производственная задача №3

Задача №2 Оптимальная организация рекламной компании №7

Задача №3 Транспортная задача №8

Задача №4 Задача об оптимальном назначении№8

Задача №1 Производственная задача

Постановка задачи.

При производстве трех видов продукции используют два типа сырья. Составить план выпуска продукции, обеспечивающий максимум прибыли. Исходные данные таковы:

Таблица 1.1

Экономико-математическая модель.

Обозначим за 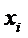(i =1….3) объем производства соответствующей продукции.

С учетом значений задачи получаем.

4х₁ + 5х₂ + 1х₃ ≤ 40

2х₁ + 1х₂ + 3х₃ ≤ 24

Дополнительные ограничения:

, , .

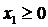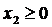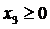Необходимо найти оптимальный план выпуска продукций (т.е. 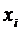), который обеспечит максимальную выручку.

Исходя из условий задачи целевая функция принимает вид:

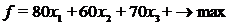
Табличная модель.

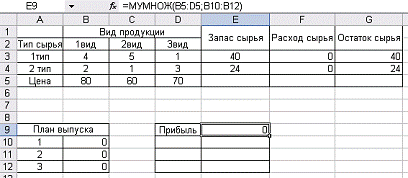
Рис. 1.1. Табличное представление модели

Более наглядно заполнение ячеек табличной формы задачи представлено на рисунке 1.2.

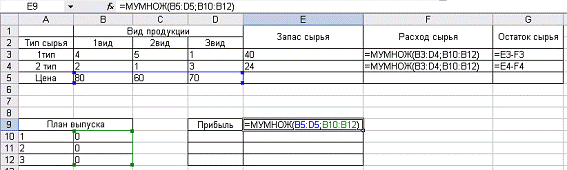
Рис. 1.2. Табличная модель с представленными формулами

Оптимизация. Сервис  Поиск решений.

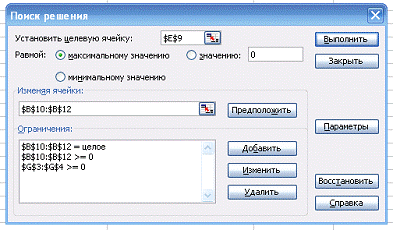
Рис. 1.3. Диалоговое окно надстройки Поиск решения

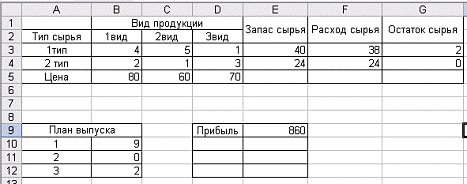
Рис. 1.4. Решение производственной задачи

Вывод: Оптимальный план производства, при данных условиях, состоит в том, что продукцию 1-ого и 3-ого видов необходимо производить в объеме 9 и 2 ед. соответственно, а продукции 2-ого вида не выпускать в производство. При этом обеспечивается максимальная выручка в размере 860 д.е.

Задача №2 Оптимальная организация рекламной компании

Постановка задачи.

На рекламу выделено 80000 руб. Предприятие рекламирует свою деятельность, используя четыре источника массовой информации: Интернет, телевидение, радио, газеты. Анализ рекламной деятельности в прошлом показал, что вложенные в рекламу средства приводят к увеличению прибыли на 16, 14, 9, 8 руб соответственно, в расчете на 1 руб, затраченный на рекламу. Руководство намерено потратить половину суммы на рекламу на телевидении, не менее 20% выделенной суммы - на радио, не более 25% - на газеты. Определить оптимальное распределение средств, направляемых на рекламу.

Экономико-математическая модель.

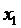- средства, направленные на Интернет;

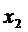- средства, направленные на телевидение;

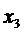- средства, направленные на радио;

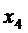- средства, направленные на газеты.

Ограничения:

х₁ + х₂ + х₃ + х₄ = 80000,

х₂ ≤ 0,5 * 80000,

х₃ ≥ 0,2 * 80000

х₄ ≤ 0,25 * 80000

х₁ ≥ 0, х₂ ≥ 0, х₃ ≥ 0, х₄ ≥ 0.

Табличная модель.

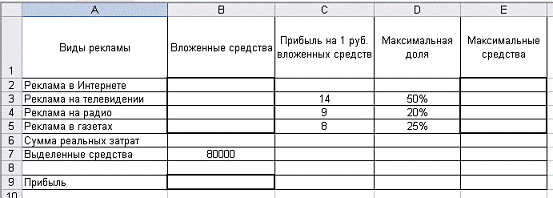
Рис. 2.1 Табличное представление модели

Рис. 2.2 Табличная модель с представленными формулами

Оптимизация. Сервис 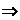 Поиск решения.

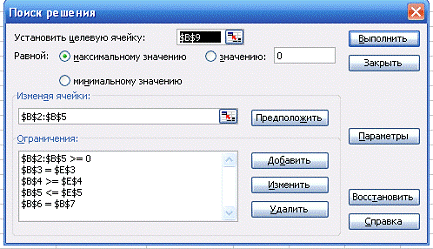
Рис. 2.3 Диалоговое окно надстройки Поиск решения

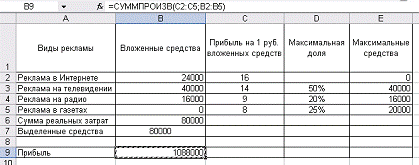
Рис. 2.4 Решение задачи об оптимальной организации рекламной компании

Вывод: Для получения максимальной прибыли, предприятие, проводя рекламную компанию, должно вложить 24000 руб. на рекламу - в Интернете, 40000 руб. в рекламу на телевидении, 16000 р. - в рекламу на радио, и не вкладывать средства на рекламу в газетах. При этом максимальная прибыль составит 1088000 руб.

Задача №3 Транспортная задача

Постановка задачи.

Фирма по доставке букетов цветов имеет шесть постоянных клиентов. Цветы поставляются из четырех киосков, где ежедневный запас составляет: 10, 20, 10, 30 букетов соответственно. Фирма получила заказ от постоянных клиентов: А, В, D, E, F по 10 букетов, C - 20 букетов. Удельные затраты на поставку букетов от каждого киоска каждому клиенту представлены в таблице. Определить объем поставки из каждого киоска каждому клиенту так, чтобы минимизировать суммарные затраты.

Экономико-математическая модель.

Искомый объем перевозки от i-ого поставщика к j-ому потребителю обозначим через 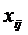. Тогда определяются ограничения для условия реализации всех мощностей:

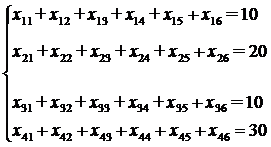
Ограничения для удовлетворения спросов всех потребителей:

х₁₁ + х₂₁ + х₃₁ + х₄₁ = 10

х₁₂ + х₂₂ + х_{3 2}+ х₄₂ = 10

х₁₃ + х₂₃+ х₃₃ + х₄₃ = 20

х₁₄ + х₂₄ + х₃₄ +х₄₄ = 10

х₁₅ + х₂₅ + х₃₅ + х₄₅ = 10

х₁₆ + х₂₆ +х₃₆ + х₁₆ = 10

Суммарные затраты на перевозку выражаются через коэффициенты затрат и поставки и определяют целевую функцию.

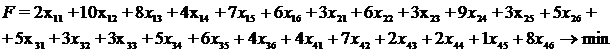
Табличная модель.

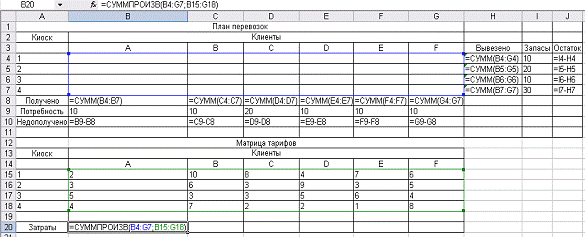
Рис. 3.2. Табличная модель с представленными формулами

Оптимизация. Сервис  Поиск решения.

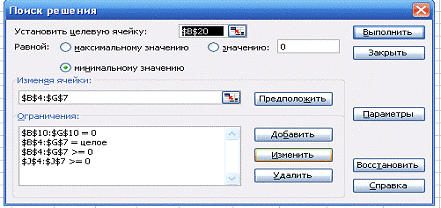
Рис. 3.3. Диалоговое окно надстройки Поиск решения

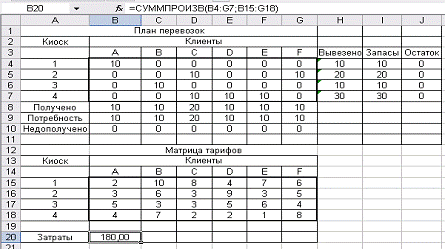
Рис. 3.4. Решение транспортной задачи

Вывод:  Минимальные суммарные затраты на доставку букетов цветов в размере 180 д.е. достигаются путем распределения поставок, представленных в ячейках [B4:G4]и[B6:G6] . Так, например, киоск 2 должен доставить клиенту C 10 ед. букетов и клиенту F 10ед. букетов. К клиентам A, В, D, E ехать не надо. А киоск 4 должен доставить клиентам C, D, E, по 10 ед. букетов. А к клиентам A, B, F ехать не надо.

Задача №4 Задача об оптимальном назначении

Постановка задачи.

На упаковочной поточной линии работают четыре сотрудника. Операции упаковки последовательны. Время работы (в мин.) каждого сотрудника на каждой операции представлено в таблице. Необходимо наладить процесс упаковки так, чтобы сократить общее время упаковки (повысить производительность).

Экономико-математическая модель. Данная задача является типичной моделью линейного целочисленного программирования (Ц.Л.П.), так как включает в себя двойственные ограничения на переменные (1- сотрудник назначается на должность, 0- сотрудник не назначается на должность).

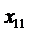- сотрудник A назначается на должность № 1;

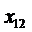- сотрудник A назначается на должность № 2;

х₁₃ - сотрудник A назначается на должность № 3;

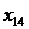- сотрудник A назначается на должность № 4;

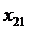- сотрудник B назначается на должность № 1;

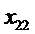 - сотрудник B назначается на должность № 2;

х₂₃ - сотрудник B назначается на должность № 3;

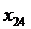- сотрудник B назначается на должность № 4;

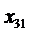- сотрудник C назначается на должность № 1;

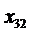- сотрудник C назначается на должность № 2;

х₃₃ - сотрудник C назначается на должность № 3;

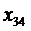- сотрудник C назначается на должность № 4;

х ₄₁- сотрудник D назначается на должность № 1;

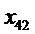 - сотрудник D назначается на должность № 2;

х₄₃ - сотрудник D назначается на должность № 3;

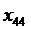- сотрудник D назначается на должность № 4;

Имеем матрицу переменных:

х₁₁ х₁₂ х₁₃ х₁₄

х₂₁ х₂₂ х₂₃ х₂₄

х₃₁ х₃₂ х₃₃ х₃₄

х₄₁ х₄₂ х₄₃ х₄₄

Целевая функция выражает суммарную производительность и имеет вид:

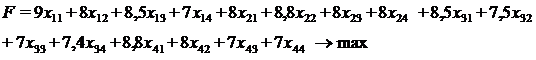
Ограничения:

Матрица переменных принимает двоичное значение:

1 сотрудник назначается на должность;

0- сотрудник не назначается на должность.

Табличная модель.

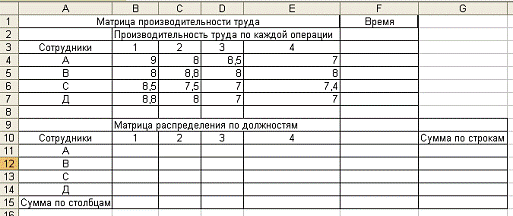
Рис. 4.1. Табличное представление модели

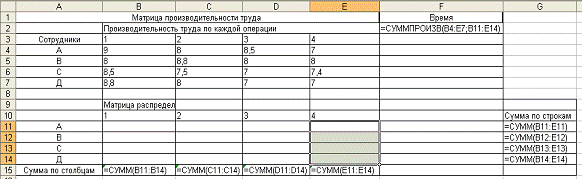
Рис. 4.2. Табличная модель с представленными формулами

Оптимизация. Сервис  Поиск решения.

Рис. 4.3Диалоговое окно надстройки Поиск решения

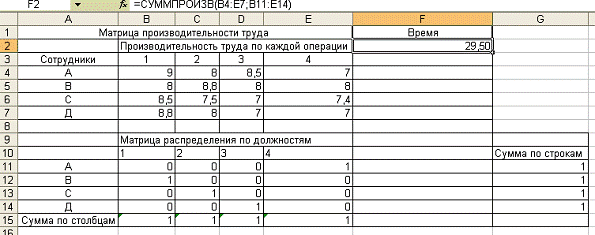
Рис. 4.4. Решение задачи об оптимальном назначении

Вывод: С учетом производительности труда всех работников по каждой операции, менеджеру необходимо назначить: сотрудника A на должность № 4, сотрудника B на должность №1, сотрудника C на должность №2, сотрудника D на должность №3,. При этом коллектив добьется общей времени упаковки 29,50 мин.