Примеры решения задач по статистике
Вариант
3.
1.
Какая шкала
называется шкалой интервалов? Приведите примеры.
Измерение
– это приписывание числовых форм объектам или событиям в соответствии с
определенными правилами (Стивене С.. i960, с60) С.Стивенсом предложена
классификация из 4 типов шкал измерения:
1.
номинативная, или
номинальная, или шкала наименований;
2.
порядковая, или
ординальная, шкала;
3.
интервальная, или
шкала равных интервалов;
4.
шкала равных
отношений.
Интервальная
шкала – это шкала,
классифицирующая по принципу "больше на определенное количество единиц -
меньше на определенное количество единиц". Каждое из возможных значений
признака стоит от другого на равном расстоянии.
Можно
предположить, что если мы измеряем время решения задачи в секундах, то это уже
явно шкала интервалов. Однако на самом деле это не так, поскольку
психологически различие в 20 секунд между испытуемым А и Б может быть отнюдь не
равно различию в 20 секунд между испытуемыми Б и Г, если испытуемый А решил
задачу за 2 секунды, Б - за 22, В - за 222, а Г - за 242.
Аналогичным
образом, каждая секунда после истечения полутора минут в опыте с измерением
мышечного волевого усилия на динамометре с подвижной стрелкой, по
"цене", может быть, равна 10 или даже более секундам в первые
полминуты опыта. "Одна секунда за год идет" - так сформулировал это
однажды один испытуемый.
Попытки
измерять психологические явления в физических единицах - волю в способности в
сантиметрах, а ощущение собственной недостаточности - в миллиметрах и т. п.,
конечно, понятны, ведь все-таки это измерения в единицах "объективно"
существующего времени и пространства. Однако ни один опытный исследователь при
этом не обольщает себя мыслью, что он совершает измерения по психологической
интервальной шкале. Эти измерения принадлежат по-прежнему к шкале порядка,
нравится нам это или нет (Стивенс С., I960, с.56; Паповян С.С., 1983, с.63;
Михеев В.И., 1986, с.28).
Мы
можем с определенной долей уверенности утверждать лишь, что испытуемый А решил
задачу быстрее Б, Б быстрее В, а В быстрее Г.
Аналогичным
образом, значения, полученные испытуемыми в баллах по любой нестандартизованной
методике, оказываются измеренными лишь по шкале порядка. На самом деле
равноинтервальными можно считать лишь шкалы в единицах стандартного отклонения
и процентные шкалы, и то лишь при условии, что распределение значений в
стандартизующей выборке было нормальным (Бурлачу Л.Ф., Морозов С.М., 1989.
с.163, с.101).
Принцип
построения большинства интервальных шкал построен на известном правиле
"трех сигм": примерно 97,7-97,8% всех значений признака при
нормальном его распределении укладываются в диапазоне М±Зσ[1].
Можно построить шкалу в единицах долей стандартного отклонения, которая будет
охватывать весь возможный диапазон изменения признака, если крайний слева и
крайний справа интервалы оставить открытыми.
Р.Б. Кеттелл
предложил, например, шкалу стеков - "стандартной десятки*. Среднее
арифметическое значение в "сырых" баллах принимается за точку
отсчета. Вправо и влево отмеряются интервалы, равные 1/2 стандартного
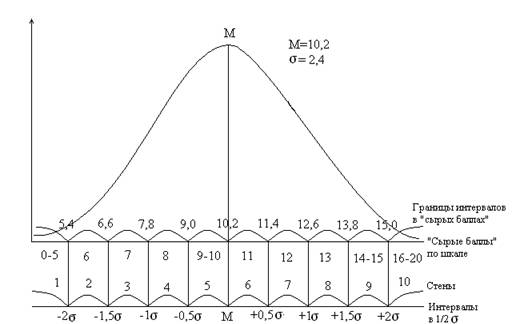
отклонения. На рис. 1.1 представлена схема вычисления стандартных оценок и
перевода "сырых" баллов в стены по шкале N 16-факторного личностного
опросника Р.Б. Кеттелла.
\
Рис.
1.1. Схема вычисления стандартных оценок (стенов) по фактору N 16-факторного личностного опросника Р.Б.
Кеттелла; внизу указаны интервалы в единицах ½ стандартного отклонения
В
принципе, шкалу стенов можно построить по любым данным, измеренным по крайней
мере в порядковой шкале, при объеме выборки п>200 и нормальном распределении
признака.
2.
Простая
случайная выборка
состоит из подмножества заданной совокупности (популяции), позволяющего делать
более или менее точные выводы относительно совокупности в целом.
3.
СРЕДНЕЕ
АРИФМЕТИЧЕСКОЕ -
один из показателей центра распределения для количественных переменных;
обозначается x. Представляет собой значение переменной, полученной в
результате деления суммы всех ее значений на объем выборки:
x = ∑ni=1 xi
/ n,
где xi
- значение переменной X с номером i;
n - объем выборки.
Например, для выборки из
9 значений - 27, 29, 30, 30, 32, 37, 46, 50, 52 - С.А. будет равно:
x = (27 + 29 + 30 + 32 +
37 + 46 + 50 + 52) / 9 = 37.
Если переменная принимает
дискретное значение и ее значения повторяются, С.А. может быть вычислено по
формуле:
x = ∑ki=1
xifi / ∑ki=1 fi
,
где xi
- значение переменной Х с номером i;
fi - частота, соответствующая значению xi;
k - количество значений переменной;
∑ki=1
fi= n - объем выборки.
Для приведенной ниже
таблицы:
x = (1 × 15 + 2
× 30 + 3 × 40 + 4 × 25 + 5 × 10) / 120 = 2,9 (балла).
|
значения (xi)
|
1
|
2
|
3
|
4
|
5
|
∑
|
|
частоты (fi)
|
15
|
30
|
40
|
25
|
10
|
120
|
4.
Объяснить, что
такое уровень статистической значимости.
Уровень
значимости – это вероятность того, что мы сочли различия существенными, а они
на самом деле случайны.
Когда
мы указываем, что различия достоверны на 5%-ом уровне значимости, или при p≤0,05. то мы имеем виду, что
вероятность того, что они все-таки недостоверны, составляет 0,05. Когда мы
указываем, что различия достоверны на 1%-ом уровне значимости, или при p≤0,01, то мы имеем в виду, что
вероятность того, что они все-таки недостоверны, составляет 0,01.
Если
перевести все это на более формализованный язык, то уровень значимости - это
вероятность отклонения нулевой гипотезы, в то время как она верна.
В статистике величину
называют статисти́чески зна́чимой, если мала вероятность чисто
случайного возникновения её или ещё более крайних величин. Здесь под крайностью
понимается степень отклонения от нуль-гипотезы. Разница называется «статистически
значимой», если имеются данные, появление которых было бы маловероятно, если
предположить, что эта разница отсутствует; это выражение не означает, что
данная разница должна быть велика, важна, или значима в общем смысле этого
слова.
Уровень значимости обыкновенно
обозначают греческой буквой α (альфа). Популярными уровнями значимости
являются 5%, 1%, и 0.1%. Если тест выдаёт p-величину меньше α-уровня, то
нуль-гипотеза отклоняется. Такие результаты неформально называют «статистически
значимыми». Например, если кто-то говорит что «шансы того, что случившееся
является совпадением, равны одному из тысячи», то имеется в виду 0.1 %
уровень значимости.
5.
Как
интерпретировать моду, медиану и среднее?
Мода — точка, в
которой плотность
распределения имеет локальный максимум. Распределение может иметь
несколько мод.
МЕДИАНА - один из
показателей центра распределения для порядковых и количественных переменных;
обозначается Ме. Представляет собой значение переменной, которое делит
выборку пополам таким образом, чтобы для 50% объектов из выборки значения
переменной не превосходили Ме, а для других 50% объектов - были не
меньше, чем Ме.
Математи́ческое
ожида́ние — понятие среднего значения
случайной величины
в теории вероятностей.
Все рассмотренные характеристики: мода, медиана, средняя арифметическая,
среднее взвешенное ѕ являются средними. Они характеризуют центральные тенденции
одномерного распределения.
6.
Квантильная
шкала – это шкала,
условием для построения которой является возможность ранжирования испытуемых по
величине у.
Квантильные ранги имеют
прямоугольное распределение, то есть в каждом интервале квантильнои шкалы
содержится одинаковая доля обследованных лиц. Стандартизация тестовых оценок
путем их перевода в квантильную шкалу стирает различия в особенностях
распределения психодиагностических показателей, так как сводит любое
распределение к прямоугольному. Поэтому с позиции теории измерений квантильные
шкалы относятся к шкалам порядка: они дают информацию, у кого из испытуемых
сильнее выражено тестируемое свойство, но ничего не позволяют сказать о том,
насколько или во сколько раз сильнее.
7.
Если
коэффициент корреляции по модулю оказывается близким к единице, то исследуемые величины линейно
зависимы.
8.
Решить
задачу, используя критерий Фридмана.
Шести респондентам
предъявлялся тест Равенна. Фиксируется время решения каждого задания.
Экспериментатор предполагает, что будут найдены статистически значимые различия
между временем решения первых трёх заданий. Результаты замеров представлены в
таблице.
|
№ п/п
|
Время решения 1-ого задания теста, сек.
|
Время решения второго задания теста, в сек.
|
Время решения третьего задания теста в сек.
|
|
1
|
8
|
3
|
|
2
|
4
|
15
|
12
|
|
3
|
6
|
23
|
15
|
|
4
|
3
|
6
|
6
|
|
5
|
7
|
12
|
3
|
|
6
|
15
|
24
|
12
|
|
Суммы
|
43
|
83
|
53
|
|
Средние
|
7,2
|
13,8
|
8,8
|
Решение
Критерий
χ2r Фридмана
Назначение
критерия
Критерий
χ2r применяется
для сопоставления показателей, измеренных в трех или более условиях на одной и
той же выборке испытуемых.
Критерий
позволяет установить, что величины показателей от условия к условию изменяются,
но при этом не указывает на направленность изменений.
Гипотезы
H0: Между показателями, полученными
(измеренными) в разных условиях, существуют лишь случайные различия.
H1: Между показателями, полученными в
разных условиях, существуют неслучайные различия.
Проранжируем
значения, полученные по трем тестам каждым испытуемым.
Сумма
рангов по каждому испытуемому должна составлять 6. Расчетная общая сумма рангов
в критерии определяется по формуле:
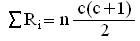
где n - количество испытуемых
с -
количество условий измерения (замеров).
В
данном случае,
6*3*(3+1)/2
= 36
Показатели
времени решения тестов 1, 2, 3 и их ранги (n=6)
|
№ п/п
|
Тест 1
|
Тест 2
|
Тест 3
|
|
Время решения 1-ого задания теста, сек.
|
Ранг
|
Время решения 2-ого задания теста, в сек.
|
Ранг
|
Время решения 3-его задания теста в сек.
|
Ранг
|
|
1
|
8
|
3
|
3
|
1
|
5
|
2
|
|
2
|
4
|
1
|
15
|
3
|
12
|
2
|
|
3
|
6
|
23
|
3
|
15
|
2
|
|
4
|
3
|
1
|
6
|
3
|
6
|
2
|
|
5
|
7
|
2
|
12
|
3
|
3
|
1
|
|
6
|
15
|
2
|
24
|
3
|
12
|
1
|
|
Суммы
|
43
|
10
|
83
|
16
|
53
|
10
|
|
Средние
|
7,2
|
|
13,8
|
|
8,8
|
|
Общая
сумма рангов составляет: 10+16+10=36, что совпадает с расчетной величиной.
Сформулируем
гипотезы.
Н0:
Различия во времени, которое испытуемые проводят над решением трех различных тестов,
являются случайными.
H1: Различия во времени, которое
испытуемые проводят над решением трех различных тестов, не являются случайными.
Теперь
нам нужно определить эмпирическое значение χ2r, по формуле:
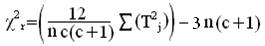
где с
- количество условий;
n - Количество испытуемых;
T2j - суммы рангов по каждому из условий.
Определим
χ2r
для данного случая:
χ2r = ((12/6*3*(3+1))*(100 +256 + 100)) –
3*6*(3+1) = 4
Поскольку
в данном примере рассматриваются три задачи, то есть 3 условия, с=3. Количество
испытуемых n=6. Это позволяет нам воспользоваться
специальной таблицей χ2r, а именно табл. VII-A
Приложения I. Эмпирическое значение χ2r=4 при с=3, n=6 точно соответствует уровню значимости р=0,184.
Ответ: Н0 отклоняется. Принимается
Н1. Различия во времени, которое испытуемые проводят над решением
трех различных тестов, неслучайны (р=0,184).
9.
Решить
задачу, используя критерий Розенбаума.
Экспериментатор измерил,
используя тест Векслера, показатели интеллекта у двух групп респондентов из
городской и сельской местности. Его интересует вопрос – будут ли обнаружены
статистические значимые различия в показателях интеллекта. В городской группе
было 11 человек, в сельской – 12.
|
город
|
96
|
100
|
104
|
104
|
120
|
120
|
120
|
120
|
126
|
130
|
134
|
|
|
село
|
76
|
82
|
82
|
84
|
88
|
100
|
102
|
Ё04
|
110
|
118
|
120
|
Решение
Таблица
1.
Индивидуальные
значения вербального интеллекта в выборках городских (n1=11) и сельских (n2=12 )
респондентов
|
Город
|
Показатель вербального интеллекта
|
Село
|
Показатель вербального интеллекта
|
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
|
8.
|
|
|
9.
|
|
|
10.
|
|
|
11.
|
|
|
|
|
|
|
|
|
|
|
|
|
96
|
|
100
|
|
104
|
|
104
|
|
120
|
|
120
|
|
120
|
|
120
|
|
126
|
|
130
|
|
134
|
|
|
|
|
|
|
|
|
1.
|
|
|
2.
|
|
|
3.
|
|
|
4.
|
|
|
5.
|
|
|
6.
|
|
|
7.
|
|
8.
|
|
|
9.
|
|
|
10.
|
|
|
11.
|
|
|
12.
|
|
|
|
76
|
|
82
|
|
82
|
|
84
|
|
88
|
|
96
|
|
100
|
|
102
|
|
104
|
|
110
|
|
118
|
|
120
|
|
Упорядочим
значения в обеих выборках, а затем сформулируем гипотезы:
H0: горожане
не превосходят сельчан по уровню вербального интеллекта.
H1: горожане
превосходят сельчан по уровню вербального интеллекта.
Таблица
2
Упорядоченные
по убыванию вербального интеллекта ряды индивидуальных значений в двух выборках
|
1 ряд – горожане
|
2 ряд – сельчане
|
|
1
2
3
|
|
134
130
126
|
S1
|
|
4
5
6
7
8
9
10
11
|
.
|
120
120
120
120
104
104
100
96
|
|
|
|
|
|
|
|
|
|
|
1
2
3
4
5
6
7
|
120
118
110
104
102
100
96
|
|
|
8
9
10
11
12
|
88
84
82
82
76
|
|
S2
|
|
Как
видно из табл. 2, мы правильно обозначили ряды: первый тот, что
"выше" - ряд горожан, а второй, тот, что "ниже” - ряд сельчан. По
табл. 2. определяем количество значений первого ряда, которые больше
максимального значения второго ряда: S1=3. Теперь
определяем количество значений второго ряда, которые меньше минимального
значения первого ряда: S2=5. Вычисляем по формуле:
Qэмп =S1+S2=3 + 5 =8
По
табл.1 Приложения 1 определяем критические значения Q для n1=11, n2=12;
|
Правило
отклонения Н0 в принятия Н1
Если
эмпирическое значение критерия равняется критическому значению,cответствующему р≤0,05 или
превышает его, то Н0 отклоняется, но мы еще не можем определенно
принять Н1.
Если
эмпирическое значение критерия равняется критическому значению,
соответствующему р≤0,01 или превышает его, то Н0 отклоняется
и принимаетсяH1.
|

Рис
1. ось значимости для критерии Q
Разенбаума
Эмпирическое
значение критерия попадает в область между Q0,05 и Q0,01. Это зона
"неопределенности": мы уже можем отклонить гипотезу о недостоверности
различий (Н0), но еще не можем принять гипотезы об их достоверности
(H1).
Ответ: мы уже можем отклонить гипотезу о
недостоверности различий интеллекта между городскими и сельскими жителями(Н0),
но еще не можем принять гипотезы об их достоверности (H1).
10.
Как
рассчитать коэффициент корреляции Спримена, если мы имеем одинаковые ранги?
Поскольку
в обоих сопоставляемых ранговых рядах присутствуют группы одинаковых рангов,
перед подсчетом коэффициента ранговой корреляции необходимо внести поправки на
одинаковые ранги Та и Тb:
Та=∑(а3-а)/12
Тb=∑(b3-b)/12
где a - объем каждой группы одинаковых
рангов в ранговом ряду А,
b - объем каждой группы одинаковых
рангов в ранговом ряду В.
Для
подсчета эмпирического значения гs используем формулу:
rs=1-6
При
больших количествах одинаковых рангов изменения rs могут оказаться гораздо более
существенными. Наличие одинаковых рангов означает меньшую степень
днфферентдкрованностк упорядоченных переменных и, следовательно, меньшую
возможность оценить степень связи между ними.
[1] Определения и формулы
расчета М и σ даны в параграфе «Распределение признака. Параметры
распределения».