Исследование цепи однофазного синусоидального напряжения с параллельным соединением приемников электрической энергии
Министерство образования
Российской Федерации
Пермский Государственный
Технический Университет
Кафедра электротехники и
электромеханики
Лабораторная работа
«Исследование цепи
однофазного синусоидального напряжения с параллельным соединением приёмников
электрической энергии»
Цель работы
Изучение
процессов в электрической цепи с параллельным соединением приёмников,
содержащих индуктивные и емкостные элементы, при различном соотношении их
параметров. Опытное определение условий достижения в данной цепи явления
резонанса тока.
Табл. 1.
Паспортные данные электроизмерительных приборов.
|
№
п/п
|
Наименованное
прибора
|
Заводской
номер
|
Тип
|
Система
измерения
|
Класс
точности
|
Предел
измерений
|
Цена деления
|
|
1
|
Вольтметр
|
|
Э34
|
ЭМ
|
1.0
|
300 В
|
10 В
|
|
2
|
Вольтметр
|
|
Э34
|
ЭМ
|
1.0
|
300 В
|
10 В
|
|
3
|
Амперметр
|
|
Э30
|
ЭМ
|
1.5
|
5 А
|
0.2 А
|
|
4
|
Амперметр
|
|
Э30
|
ЭМ
|
1.5
|
5 А
|
0.2 А
|
|
5
|
Амперметр
|
|
Э30
|
ЭМ
|
1.5
|
5 А
|
0.2 А
|
|
6
|
Ваттметр
|
|
Д539
|
ЭД
|
0.5
|
6000 Вт
|
40 Вт
|
Теоретические
сведения
На рис. 1
представлена электрическая цепь однофазного синусоидального напряжения с
параллельным соединением 2-х приемников, один из которых на схеме замещен
последовательным со-единением резистора и емкостного элемента, а второй –
последовательным соединением резистора и индуктивного элемента. Токи в
приемниках определяются по закону Ома:
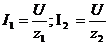
где U –
действующее значение напряжения источника электрической энергии;
r1,
xC1, z1 – активное, емкостное и полное сопротивления
первого приемника;
r2,
xL2, z2 – активное, емкостное и полное сопротивления
второго приемника;
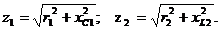
Вектор тока
источника электрической энергии равен сумме векторов токов приёмников:
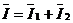
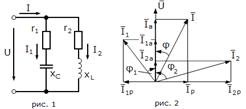
Векторная
диаграмма напряжений и токов для рассматриваемой схемы приведена на рис. 2
Энергетические
процессы в электрической цепи характеризуются величинами активной P, реактивной
Q и полной S мощности, а также коэффициентам мощности cosφ.
Для первого
приёмника
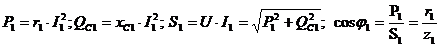
Для второго
приёмника
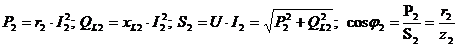
Для двух
приёмников
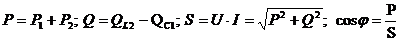
В
соответствии с балансом активной и реактивной мощностей под P, Q, S, cosφ
следует пони-мать также активную, реактивную и полную мощности источника
электрической энергии и его коэффициент мощности.
Величины
активной и реактивной составляющих токов приемников (см. рис. 2):
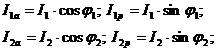
где φ1
и φ2 – углы сдвига фаз между вектором напряжения 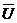 и векторами токов
и векторами токов 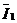 и
и 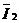 .
.
Представление
токов активными и реактивными составляющими позволяет путем их сложения найти
активную Iа и реактивную Iр составляющие тока источника и
по ним определить ток источника I:
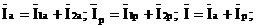
Из векторной
диаграммы рис. 2, следует:
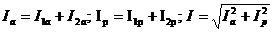
Косинус угла
сдвига фаз между вектором тока источника и вектором напряжения источника
определяется из выражения:
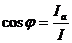
В
электрических цепях с параллельным соединением приемников, содержащих
индуктивные и емкостные элементы, может при определенных условиях возникать
явление резонанса токов. Резонансом токов называется режим, при котором ток
источника электрической энергии совпадает по фазе с напряжением источника, т.е.
φ = 0. Следовательно, условием резонанса токов является
равенство нулю реактивной мощности цепи и реактивной составляющей тока
источника электрической энергии.
Из условия
резонанса токов следует, что
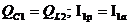
При резонансе
токов коэффициент мощности цепи
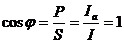
Ток в ветви с
источником электрической энергии содержит только активную составляющую,
является минимальным по величине и может оказаться значительно меньше токов в
каждом из параллельно включенных приемников:
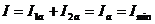
Рабочее
задание
1. Собираем
схему, изображенную на рис. 3.
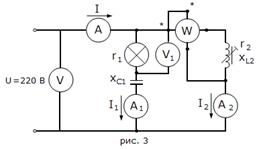
2. Медленно
выдвигая сердечник, снимаем показания приборов для трех точек до резонанса,
точки в околорезонансной области и шести точек после резонанса. Показания
приборов заносим в табл. 2.
Табл. 2.
Опытные данные.
|
№
|
U
|
U1
|
I
|
I1
|
I2
|
PК2
|
|
В
|
А
|
кол. дел.
|
Вт
|
|
1
|
215
|
110
|
1,35
|
2,1
|
1
|
1,5
|
15
|
|
2
|
215
|
110
|
1,25
|
2,1
|
1,4
|
2
|
20
|
|
3
|
215
|
110
|
1,22
|
2,1
|
1,6
|
3
|
30
|
|
4
|
215
|
110
|
1,28
|
2,1
|
1,8
|
4
|
40
|
|
5
|
215
|
110
|
1,3
|
2,1
|
2
|
4,5
|
45
|
|
6
|
215
|
110
|
1,42
|
2,1
|
2,4
|
6
|
60
|
|
7
|
215
|
110
|
1,78
|
2,1
|
2,8
|
8
|
80
|
|
8
|
215
|
110
|
2,1
|
2,1
|
3,2
|
10
|
100
|
|
9
|
215
|
110
|
2,5
|
2,1
|
3,6
|
12,5
|
125
|
|
10
|
215
|
110
|
2,9
|
2,1
|
4
|
15
|
150
|
|
11
|
215
|
110
|
3,35
|
2,1
|
4,4
|
18
|
180
|
|
12
|
215
|
110
|
3,9
|
2,1
|
5
|
23,5
|
235
|
3. По
результатам опытов вычисляем величины, входящие в табл. 3.
Табл. 3.
Расчетные данные
|
№
|
P1
|
S1
|
QC1
|
cos φ1
|
S2
|
QL2
|
cos φ2
|
xL2
|
P
|
S
|
cos φ
|
L
|
|
Вт
|
ВА
|
ВАр
|
о.е.
|
ВА
|
ВАр
|
о.е.
|
Ом
|
Вт
|
ВА
|
о.е.
|
Гн
|
|
1
|
231
|
451,5
|
387,93
|
0,5116
|
215
|
214,48
|
0,070
|
214,48
|
246
|
290,25
|
0,848
|
0,683
|
|
2
|
231
|
451,5
|
387,93
|
0,5116
|
301
|
300,33
|
0,066
|
153,23
|
251
|
268,75
|
0,934
|
0,488
|
|
3
|
231
|
451,5
|
387,93
|
0,5116
|
344
|
342,69
|
0,087
|
133,86
|
261
|
262,30
|
0,995
|
0,426
|
|
4
|
231
|
451,5
|
387,93
|
0,5116
|
387
|
384,93
|
0,103
|
118,80
|
271
|
275,20
|
0,985
|
0,378
|
|
5
|
231
|
451,5
|
387,93
|
0,5116
|
430
|
427,64
|
0,105
|
106,91
|
276
|
279,50
|
0,987
|
0,340
|
|
6
|
231
|
451,5
|
387,93
|
0,5116
|
516
|
512,50
|
0,116
|
88,98
|
291
|
305,30
|
0,953
|
0,283
|
|
7
|
231
|
451,5
|
387,93
|
0,5116
|
602
|
596,66
|
0,133
|
76,10
|
311
|
382,70
|
0,813
|
0,242
|
|
8
|
231
|
451,5
|
387,93
|
0,5116
|
688
|
680,69
|
0,145
|
66,47
|
331
|
451,50
|
0,733
|
0,212
|
|
9
|
231
|
451,5
|
387,93
|
0,5116
|
774
|
763,84
|
0,161
|
356
|
537,50
|
0,662
|
0,188
|
|
10
|
231
|
451,5
|
387,93
|
0,5116
|
860
|
846,82
|
0,174
|
52,93
|
381
|
623,50
|
0,611
|
0,168
|
|
11
|
231
|
451,5
|
387,93
|
0,5116
|
946
|
928,72
|
0,190
|
47,97
|
411
|
720,25
|
0,571
|
0,153
|
|
12
|
231
|
451,5
|
387,93
|
0,5116
|
1075
|
1049,00
|
0,219
|
41,96
|
466
|
838,50
|
0,556
|
0,134
|
Вычислим эти
величины для первого опыта:
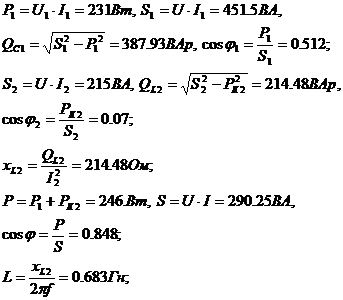
 Для остальных случаев
вычисления аналогичны
Для остальных случаев
вычисления аналогичны
4. Используя
данные табл. 2 и табл. 3 рассчитаем активные и реактивные составляющие то-ков
всех ветвей:
Для первого
опыта:
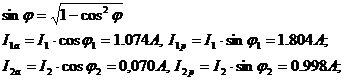
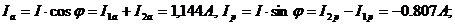
Для остальных
случаев вычисления аналогичны
Данные
расчета занесены в табл. 4. В этой же таблице представлены численные значения
индуктивности из табл. 3.
Табл. 4. Расчетные
данные.
|
№
|
L
|
I1a
|
I1p
|
I2a
|
I2p
|
Ia
|
Ip
|
|
Гн
|
А
|
|
1
|
0,683
|
1,074
|
1,804
|
0,070
|
0,998
|
1,144
|
-0,807
|
|
2
|
0,488
|
1,074
|
1,804
|
0,093
|
1,397
|
1,167
|
-0,407
|
|
3
|
0,426
|
1,074
|
1,804
|
0,140
|
1,594
|
1,214
|
-0,210
|
|
4
|
0,378
|
1,074
|
1,804
|
0,186
|
1,790
|
1,260
|
-0,014
|
|
5
|
0,340
|
1,074
|
1,804
|
0,209
|
1,989
|
1,284
|
0,185
|
|
6
|
0,283
|
1,074
|
1,804
|
0,279
|
2,384
|
1,353
|
0,579
|
|
7
|
0,242
|
1,074
|
1,804
|
0,372
|
2,775
|
1,447
|
0,971
|
|
8
|
0,212
|
1,074
|
1,804
|
0,465
|
3,166
|
1,540
|
1,362
|
|
9
|
0,188
|
1,074
|
1,804
|
0,581
|
3,553
|
1,656
|
1,748
|
|
10
|
0,168
|
1,074
|
1,804
|
0,698
|
3,939
|
1,772
|
2,134
|
|
11
|
0,153
|
1,074
|
1,804
|
0,837
|
4,320
|
1,912
|
2,515
|
|
12
|
0,134
|
1,074
|
1,804
|
1,093
|
4,879
|
2,167
|
3,075
|
По
вычисленным значениям строим графики зависимостей сил тока в цепи I и ветвях I1
и I2, косинуса угла сдвига фаз cos φ от индуктивности катушки
L.
Строим
векторные диаграммы токов и напряжения:
а). I1p
< I2p. Берем 9ий результат измерений: I1a =
1.074 А, I1p = 1.804 А, I2a = 0.581 А, I2p = 3.553
А, Ia = 1.656 А, Ip = 1.748 А.
б). I1p
= I2p. Берем 4ий результат измерений: I1a = 1.074
А, I1p = 1.804 А, I2a = 0.186 А, I2p = 1.790 А,
Ia = 1.26 А, Ip = -0.014 А.
в). I1p
> I2p. Берем 1ий результат измерений: I1a =
1.074 А, I1p = 1.804 А, I2a = 0.070 А, I2p = 0.998
А, Ia = 1.144 А, Ip = -0.807 А.
Вывод: при
увеличении индуктивности катушки с 130 до 425 мГн сила тока в цепи I и во второй
ветви(с катушкой) I2 стремительно падают, при этом косинус угла
сдвига возрастает. Реактивное сопротивление катушки меньше сопротивления
конденсатора, поэтому через катушку протекает больший ток, чем через
конденсатор. В этом случае цепь принимает индуктивный характер и сила тока
отстает от напряжения(векторная диаграмма а).
При
индуктивности катушки около 425 мГн сила тока в цепи принимает наименьшее
значение I = 1.22 А, а косинус угла сдвига фаз равен 1. Реактивное
сопротивление катушки и конденсатора равны, поэтому и реактивные составляющие
токов в ветвях равны, сила тока в цепи синфазна напряжению(диаграмма б).
При
дальнейшем увеличении индуктивности катушки с 425 до 685 мГн сила тока в цепи I
начинает плавно увеличиваться, а сила тока во второй ветви I2 медленно
уменьшаться, величина косинуса угла сдвига фаз падает. Реактивное сопротивление
катушки становится больше сопротивления конденсатора, поэтому через катушку
протекает меньший ток, чем через конденсатор. В этом случае цепь принимает емкостной
характер и сила тока опережает напряжение(диаграмма в).
Изменение
индуктивности катушки никак не влияет на силу тока в первой ветви I1
= const.