Формування в учнів умінь розв’язувати задачі на рух

Формування в учнів умінь розв’язувати задачі на рух

Зміст

Вступ

1. Теоретичні основи розв’язування задач на рух

1.1 Роль задач у початковому курсі математики

1.2 Місце задач на рух у системі складених задач

2. Формування умінь учнів розв’язувати задачі на рух

2.1 Аналіз системи задач на рух у підручниках з математики для 4 класу

2.2 Методика розв’язування задач на рух

2.3 Організація і зміст експериментального дослідження, аналіз його ефективності

Висновки

Список літератури

Вступ

Актуальним завданням подальшого удосконалення роботи початкової школи є підвищення якості навчання молодших школярів, зокрема підготовка їх до подальшого життя і навчання, формування уміння вчитися. Учень уміє вчитися, якщо він «сам визначає або приймає мету, поставлену вчителем, відповідно до неї планує і виконує необхідні дії, контролює та оцінює свої результати. Така розгорнутість характеризує сформовану навчальну діяльність, яка у молодшого школяра лише починає складатися» [30, 6]. Щоб успішно просуватися вперед, учні початкових класів у співробітництві з учителем повинні оволодіти повним діапазоном загальнонавчальних умінь і навичок, серед яких розв’язування задач займає провідне місце.

Обґрунтування шляхів і методів досягнення мети навчання і виховання – гармонійно і всебічно розвиненої особистості у сучасній початковій школі – є значною теоретичною і практичною проблемою [15, 17]. Суспільство, вимагаючи творчих, інтелектуальних, освічених працівників, орієнтує загальноосвітні заклади «не лише на збагачення учня змістовними знаннями, а й на розвиток його особистості, формування прийомів розумової діяльності, соціокультурної компетентності, на виявлення людей з цінними задатками». Формування такої особистості значною мірою здійснюється у навчальному процесі. Розкриттю розумових особливостей кожного у початковій школі значною мірою сприяє розв’язування задач.

Давно відомо, що вивчення математики є одним з найкращих способів розвитку й тренування розумових здібностей людини. Математика дисциплінує розум, спрямовує думки, розвиває пам'ять, фантазію, образне мислення, відчуття краси. Підручник з арифметики, написаний відомим математиком Л.П. Магницьким у 1703 p., починався такими словами: арифметика – «це мистецтво чесне, незаздрісне і всім легко зрозуміле, багатокорисне і багатопохвальне» [2, 40].

Для занять математикою дітям не потрібно ніяких особливих обдарувань, таких, як музичний слух для музиканта чи вміння чітко розрізняти кольори для художника. Навпаки, математика сама формує вміння і покращує здібності дитини. Щоправда, «розв'язання задач, особливо складних, вимагає напруження розуму, наполегливості і терпіння, але саме цього вимагатиме від дитини її майбутнє життя» [19, 21]. Тому, можливо, було б краще з перших шкільних років допомагати школярам розвивати вольові якості, які знадобляться їм у подальшому житті. Як це зробити? Підтримати у дитини впевненість у тому, що вона зможе розв'язати будь-яку задачу – треба тільки подумати, правильно поставити запитання, уявити собі ситуацію і проаналізувати її; намагатися викликати інтерес до роботи.

Навчання математики, зокрема формування вмінь розв'язувати задачі, здійснюється шляхом виконання різних завдань. У процесі розв'язування задач реалізуються цілі навчання за такими напрямками: здобуття і вдосконалення математичних знань; формування математичних вмінь; розвиток творчого і логічного мислення [38, 19].

У процесі вивчення «математика виступає перед учнями не тільки як система логічних правил і дедуктивних доведень, а й як метод пізнання, засіб розв'язування питань практичного характеру» [9, 11]. При цьому істотне значення для виконання цих завдань мають зміст і методика навчання учнів початкової школи розв'язувати задачі.

Задачі виникають під час реальних проблемних ситуацій. Останні постають тоді, коли людина (суб'єкт) в своїй діяльності, спрямованій на якийсь об'єкт, натрапляє на певні труднощі. Якщо людина усвідомлює ці труднощі і хоче подолати їх, то в ній активізується розумова діяльність. Щоб проаналізувати і описати проблемну ситуацію, людина виходить за її межі і дивиться на неї «збоку». Такий опис проблемної ситуації і є задачею [30, 26]. Задача – це вже об'єкт, який можна передавати іншій людині.

Розв'язування математичної задачі – це «процес встановлення (знаходження) зв'язків між даними величинами, між даними та шуканою величиною, формулювання цих зв'язків мовою математики у вигляді арифметичних дій, виконання послідовності дій для знаходження числового значення шуканої величини» [50, 37]. Основне завдання педагога – вчити учнів знаходити зв'язки і добирати їх послідовність для визначення невідомого числа.

Вміння розв'язувати задачі вимагає від школярів знання деяких життєвих ситуацій, залежностей між величинами, розуміння суті арифметичних дій, знання прийомів обчислень, загальних правил причинно-наслідкових зв'язків, суті та структури задачі тощо [63, 46].

У процесі навчання молодші школярі розв'язують значну кількість задач під керівництвом учителя і самостійно. Проте нерідко під кінець навчання в початкових класах у деяких учнів знання про задачі залишаються поверховими і несистематизованими. Щоб поліпшити це становище, потрібна цілеспрямована праця вчителя, чітке розуміння ним основних вимог щодо навчання учнів розв'язувати різноманітні задачі.

У навчанні математики задачам відведено особливу роль. З одного боку, вони становлять специфічний розділ програми, матеріали якого учні мають засвоїти, а з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів [60, 19–20].

Аналіз останніх досліджень з психології [2; 3; 10; 30; 50; 56 та ін.] і методики математики [6; 15; 41; 46; 62 та ін.] свідчить про те, що в проблемі навчання молодших школярів розв'язувати задачі є значні досягнення – з'ясовано можливість застосування алгебраїчного методу розв'язування задач, визначено основні напрями роботи у виробленні в учнів уміння загального підходу до розв'язування задач, виявлено доцільність опрацювання взаємно обернених задач, з'ясовано роль задач підвищеної трудності у навчанні і розвитку, уточнено класифікацію простих задач тощо. Проте є ще й нерозв'язані питання з проблеми використання математичних задач у початковій школі.

Актуальність проблеми дослідження пов’язана з тим, що у школярів середніх та старших класів виникають чималі труднощі під час розв'язування задач на рух. Однією з причин цього ми вважаємо недостатню сформованість у початкових класах понять про величини: час, відстань, швидкість та пропорційну залежність. Формувати у молодших школярів необхідні поняття можна як на матеріалі чинних підручників початкових класів, так і доповнюючи його задачами, складеними на підґрунті типових задач, призначених для учнів середніх класів. Тому слід допомогти вчителям початкових класів і студентам факультетів підготовки вчителів початкових класів усвідомити особливості розв'язування задач на рух з молодшими школярами у процесі самостійної роботи над задачами на рух, що й вплинуло на вибір нами теми дослідження.

Метою дипломної роботи є експериментальне обґрунтування методики роботи над задачами на рух у початкових класах.

Об’єкт дослідження – задачі на рух.

Предмет дослідження – методика опрацювання задач на рух у початкових класах.

Завдання дослідження:

1) Проаналізувати педагогічну та методичну літературу з проблеми дослідження.

2) Розкрити етапи роботи над текстовою задачею.

3) Обґрунтувати дидактичні особливості задач на рух.

4) Охарактеризувати методику формування вмінь учнів розв’язувати задачі на рух.

5) Організувати і провести експериментальне дослідження, проаналізувати його результати.

Новизна роботи полягає у тому, що запропоновано комплексний підхід до методики роботи над задачами на рух у початкових класах.

Практична значимість дипломної роботи обумовлюється актуальними завданнями удосконалення навчально-виховного процесу у початковій школі та необхідністю формування пізнавальних процесів у молодших школярів. Матеріали дослідження можуть бути використані вчителями початкових класів для активізації навчальної діяльності учнів на уроках математики.

Структура роботи. Дипломна робота складається із вступу, двох розділів, списку використаних джерел, додатків.

1. Теоретичні основи розв’язування задач на рух

1.1 Роль задач у початковому курсі математики

Значне місце у початковому курсі математики займає розв’язування текстових задач. Термін «задача» вживається в різних значеннях. У найширшому плані можна сказати, що задача передбачає необхідність свідомого пошуку відповідних засобів для досягнення мети, яку добре видно, але яка безпосередньо недосяжна. У психологічному аспекті задача розглядається як свідома мета, що існує в певних умовах, а дії – як процеси або акти, спрямовані на досягнення її, тобто на розв'язування задачі.

Під математичною задачею розуміють «будь-яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, створених людським розумом на основі знань про навколишній світ» [17, 28]. Арифметичною задачею називають «вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин і існує залежність, яка пов'язує ці величини як між собою, так і з шуканою» [63, 47].

У системі навчання учнів початкових класів загальноосвітньої школи переважають арифметичні задачі. Задачі на побудову, найпростіші доведення, а також завдання логічного порядку займають порівняно незначне місце. Задачі у початковому курсі математики з одного боку становлять специфічний розділ програми, матеріал якого учні мають засвоїти, а з другого – виступають як дидактичний засіб навчання, виховання і розвитку школярів. У навчанні математики задачам відведено особливу роль.

У пояснювальній записці до програми з математики говориться, що «вивчення математики у 1–4 класах здійснюється через систему доцільних задач і практичних робіт» [28, 17]. Це означає, що формування кожного нового поняття пов'язується з розв'язуванням таких задач, які допомагають усвідомити його значення чи потребують його застосування.

Початкове розкриття змісту арифметичних дій здійснюється за допомогою відповідних операцій над предметними множинами. Засобом переходу від операцій над множинами предметів до дій над натуральними числами є задачі. Розв'язуючи задачу, учні спираються на уявлення про предмети, які згадуються в умові, але оперують уже числами.

Задачі мають як навчальні, так і виховні та розвиваючі функції. Функції задач спрямовані на формування системи математичних знань, умінь і навичок на різних етапах її засвоєння.

Робота над задачами також дає можливість реалізувати ряд функцій у вивченні математики: виховну, розвивальну, дидактичну і контролюючу [5; 6; 9; 38]. Проаналізуємо ці функції детальніше.

1) Виховні функції задач спрямовані на формування в учнів наукового світогляду. Як виховний засіб задачі дають змогу пов'язати навчання з життям, ознайомити учнів із пізнавально важливими фактами, Числові дані задач характеризують успіхи економічного зростання в нашій країні, трудові досягнення колективів підприємств, показують зростання добробуту й культури українського народу. Це виховує у дітей свідоме ставлення до навчання, любов до Батьківщини, бажання зробити власний внесок у загальну справу. Внутрішня краса самої математики, оригінальність прийомів розв'язування задач збуджують у дітей естетичні почуття.

2) Під розвивальними розуміють функції задач, спрямовані на формування в учнів науково-теоретичного, зокрема функціонального, стилю мислення, на оволодіння ними прийомами розумової діяльності. У процесі розв'язування задач учні виконують різні розумові операції (аналіз, синтез, конкретизація і абстрагування, порівняння, узагальнення), висловлюють судження і міркування. Для активізації розумових дій учнів під час розв'язування задач запитання треба ставити так, щоб вони спонукали до порівнювання, зіставлення, перевірки тощо.

3) Текстові задачі, які відображують конкретні життєві ситуації, використовуються для ознайомлення учнів з певними математичними поняттями та закономірностями, для з'ясування взаємозв'язків між словом і символом, між символом і поняттям. У деяких випадках формування теоретичних знань через задачі може бути організоване у вигляді проблемної форми навчання. Навчальні функції задач виявляються також у здійсненні принципу політехнізації та в процесі контролю знань і математичного розвитку учнів.

4) Задачі є найважливішим засобом контролю й оцінки знань учнів з математики. Самостійне розв'язування учнями текстових задач як засіб оберненого зв'язку (учень – учитель) дає змогу виявляти вміння правильно обирати і виконувати арифметичні дії, судити про розвиток мислення молодших школярів.

У реалізації принципу політехнізації в навчанні математики передбачається, зокрема, розкриття особливостей дій законів та збільшення питомої ваги практичних робіт. «Розв'язуючи задачі, учні відчувають прикладне значення математики, усвідомлюють важливість математичних знань для пізнання закономірностей навколишнього світу» [17, 28]. Розв'язування задач допомагає в оволодінні кресленням і вимірюванням відрізків, обчислюванні площі фігур, в ознайомленні з такими важливими поняттями, як шлях і швидкість, продуктивність праці, врожайність, у здійсненні між-предметних зв'язків, що посилює політехнічний аспект навчання.

Згідно з чинною програмою [28], в учнів початкової школи на уроках математики мають формуватися вміння розв'язувати прості й складені задачі різних видів. На розв'язування математичних задач у кожному класі відводиться значна кількість уроків. У 1-му класі діти ознайомлюються з поняттям «задача», вчаться розв'язувати прості задачі; у 2-му класі вводяться нові задачі, які розв'язуються двома діями, – це перші складені задачі; у 3-му і 4-му класах кількість і складність складених задач збільшується. З усієї множини виокремлюють такі типи задач: на рух, на роботу, на пропорційне ділення, на знаходження четвертого пропорційного, на знаходження числа за двома різницями, геометричного змісту тощо.

Задачі кожного типу бувають і легкими, і важкими, і дуже важкими для дітей. Таким чином, потрібно спеціально готувати учнів до усвідомлення того, що не завжди, розв'язуючи задачу, можна одразу відповісти на її запитання. З цього витікає необхідність ґрунтовної підготовчої роботи до розв'язання задач на дві і більше дій і продуманої методики введення поняття «складена задача» та подальшого формування у дітей умінь розв'язувати такі задачі [5, 16].

Учитель повинен вчити дітей розв'язувати задачі. Робити це можна за допомогою різних методів. Для типових задач найефективнішим є метод поступового ускладнення, для нетипових – метод евристичних наставлянь. Задачі нового типу природно починати розв'язувати з найпростіших, доступних усім учням. Якщо майже на кожному уроці усно розв'язувати 5–6 таких задач, можна досягти гарних результатів. Поступово складність пропонованих задач має підвищуватися, але таким чином, щоб труднощі, які виникають у процесі їх розв'язання, могли долати й слабкі учні. Нічого поганого не станеться, якщо, наприклад, третьокласникам запропонувати для усного розв'язання кілька задач, які є навіть у підручнику для першого класу.

Не слід непокоїтися, що такі надлегкі задачі уповільнять розвиток більш підготовлених та кмітливих школярів. Адже йдеться лише про 5–7 хвилин деяких уроків. А роль простих задач у навчанні математики надзвичайно велика. Вони є основним засобом у формуванні поняття про арифметичні дії та величини. У процесі розв'язання простих задач учні опановують основні прийоми роботи над задачею. Високий рівень умінь розв'язувати прості задачі – необхідна умова успішного розвитку вмінь розв'язувати задачі складені. Навіть для найсильніших учнів усне розв'язання задач корисне: воно сприяє розвитку швидкості та гнучкості мислення, розумовому розвитку молодших школярів загалом [24, 76].

Оптимізація навчальних, виховних і розвивальних функцій задач можлива за умови, що учні вже мають певні уявлення про структуру задачі, володіють умінням розв'язувати задачі, які можна використовувати як дидактичний засіб. Забезпечення цих умов і є завданням розділу «Задачі» програми з математики. Мета цього розділу – «сформувати в учнів уявлення про структуру простої і складеної арифметичної задачі; ознайомити з арифметичним і алгебраїчним підходами до розв'язування задач; домогтися, щоб кожен учень умів розв'язати будь-яку просту задачу; розвинути вміння застосовувати знання про арифметичні дії і залежності між величинами для складання плану розв'язання задачі, тобто розвинути вміння розв'язувати складені задачі» [5, 13–14].

Розподіл задач за роками навчання і визначення програмного мінімуму здійснено «з урахуванням послідовності вивчення арифметичного матеріалу, об'єктивного і суб'єктивного рівнів складності задач, методичного забезпечення їх у підручниках, а також значення їх для дальшого вивчення математики» [65, 22].

Отже, «задача – це завдання, що містить певний зміст, сюжет, в якому подаються перелік кількох груп предметів, їх кількісна характеристика, що виражається числами, або перелік кількох (не менше двох) величин, їх числові значення, які знаходяться у певних відношеннях («менше» «більше», «стільки ж»)» [31, 44]. Всі числа і числові значення величин пов'язані між собою математичними залежностями. Обов'язково в тексті задачі є запитання чи пропозиції відшукати числове значення іншої, шуканої величини, яка знаходиться у зв'язку із даними величинами. Задача – це завдання, яке здебільшого формулюється словесно (письмово чи усно), на відміну від прикладів.

Приклади складають із чисел і знаків арифметичних дій. Для запису деяких прикладів використовуються дужки, які визначають порядок виконання дій. Як у прикладі, так і в задачі треба за даними числами знайти ще одне число (невідоме). Це число знаходять шляхом виконання арифметичних дій (операцій). У прикладах дії вказано, а послідовність їх виконання визначається правилами. Під час розв'язування задачі арифметичні дії, їх кількість та послідовність виконання треба визначати самостійно.

Дорослим людям, фахівцям багатьох професій доводиться розв'язувати задачі під час виконання різних робіт. Наприклад, при обчисленні ціни, вартості товару, витрати матеріалів, числових характеристик багатьох явищ. Це задачі практичного змісту. Щоб уміти їх розв'язувати, треба спочатку навчитися розв'язувати задачі, що пропонуються підручником і вчителем. Це навчальні задачі [32, 31].

У школі задачі застосовуються при вивченні математики, фізики, хімії та деяких інших навчальних предметів, у процесі їх розв'язування в учнів підвищується розумовий розвиток, формуються загальнонавчальні уміння, вони вчаться аналізувати, робити висновки, порівнювати, складати план, узагальнювати тощо.

Текстова задача складається з умови і запитання. В умові задачі є не менше двох числових даних (іноді одне з них подається неявно (приховано)), які характеризують або кількість предметів, або значення величини, або відношення між ними. В умові вказуються зв'язки між числами, а також між даними числами і шуканим числом, за допомогою яких відбувається добір арифметичних дій для розв'язання. Числові дані подаються в умові, або в умові і запитанні. Але кожну задачу можна сформулювати так, щоб усі числа були представлені тільки в умові. Попарні зв'язки між величинами можна виразити за допомогою арифметичної дії. У запитанні задачі вказується, числове значення якої величини треба знайти. Запитання задачі формулюється у вигляді питального речення зі словами скільки, на скільки, коли, о котрій годині, або у вигляді вимоги: знайти (знайди), обчислити (обчисли), дізнатися (дізнайся) [26, 19].

Задачі складаються на основі матеріалів спостережень за явищами природи, практичної діяльності людей, математичних закономірностей, інколи за казковими, фантастичними сюжетами. Під час складання задачі необхідно дотримуватися таких вимог: умова не повинна містити неправильні твердження, числові дані мають бути правдоподібними, реальними (крім задач казкового, фантастичного змісту), умова і запитання мають бути пов'язані між собою.

Розв'язати задачу – означає встановити (розкрити, відшукати, побачити, пояснити) зв'язки між даними і шуканим числами, на основі чого дібрати потрібні арифметичні дії та їх порядок виконання, знайти результати дій, а потім відповісти на запитання задачі. Відповідь задачі не відгадується, а знаходиться при виконанні потрібних дій (операцій). У процесі розв'язування задачі треба вміти пояснити (розказати), які дії і над якими числами варто виконати, в якому порядку і чому саме такі для знаходження шуканого числа (відповіді на запитання задачі) [35, 162].

Розв'язування задачі – це процес, «робота, яка включає ознайомлення з текстом задачі, роздуми (міркування) над її розв'язанням, запис чи формулювання дій та відповіді» [17, 28]. Розв'язання задачі – це запис (формулювання) порядку арифметичних дій, за допомогою яких знаходиться відповідь до задачі. Розв'язок – відповідь на запитання задачі. А ще розв'язком називають числове значення шуканої величини [22, 11–12].

Задачу, для розв'язання якої треба виконати лише одну арифметичну дію, називають простою. Якщо для розв'язання задачі треба виконати дві або більше дій (різних чи однакових), то її називають складеною (складається з кількох простих задач, бо кожна дія – це розв’язання однієї простої задачі, що входить до її складу).

Аналіз методичної літератури показує, що «вміння розв'язувати задачі вчені визначають як складне, яке включає в себе ряд простих, часткових, а саме: вміння проводити первинний аналіз тексту (уявляти задачну ситуацію), виділяти умову й вимогу, відомі й невідомі, шукану величини, конструювати простіші моделі задачної ситуації, активізувати необхідні для розв'язання теоретичні знання, перекладати залежність між даними, даними і шуканими величинами з мови словесної на математичну та ін.». Формувати вміння необхідно поступово і систематично.

А тому «важливе значення для розв'язування текстових задач у навчальному процесі має ретельний добір навчальних завдань, які мають відповідати певним загально-методичним вимогам: забезпечувати засвоєння учнями програмового матеріалу з математики і, зокрема, формувати в них знання про задачу, її склад і процес розв'язування, вчити використовувати набуті знання в різних ситуаціях; зміст завдань має відповідати темі уроку і меті вивчення матеріалу, а числові дані – програмовим вимогам; послідовність застосування вправ має сприяти свідомому засвоєнню теоретичних знань і вмінню розв'язувати задачі, розвитку прийомів розумової і творчої діяльності школярів; забезпечувати автоматизацію елементарних дій, з яких складається діяльність при розв'язуванні задач; створювати умови для узагальнення способів діяльності; відповідати логіці й структурі процесу формування вмінь; кількість вправ повинна відповідати індивідуально-психологічним особливостям школярів і бути достатньою для формування певного вміння або навички» [19, 23–24].

Отже, беручи до уваги ці вимоги, вчені виділили і експериментально перевірили систему завдань, спрямованих на формування, в учнів умінь розв'язувати текстові задачі. Ці завдання поділені на групи відповідно до мети їх застосування у навчальному процесі, форми і способу виконання.

Завдання на формування у школярів умінь розв'язувати задачі за способом виконання поділяють на повні і фрагментарні. Повні завдання спрямовані як на засвоєння і закріплення способів розв'язанні задач певних видів, так і на формування й удосконалення загальних умінь їх розв'язувати. Але якщо вчитель ставить перед собою мету виправити прогалину в уміннях школярів, виконуючи елементарні дії при розв'язуванні задач, то, в такому випадку, повні завдання займатимуть багато навчального часу. Тоді краще виділити в окрему групу потрібні фрагментарні завдання.

Фрагментарні завдання спрямовані на спеціальне формування в учнів часткових умінь: читати текст задачі, відокремлювати умову і вимогу, виділяти відомі й невідомі величини, конструювати предметні, схематичні, графічні моделі тощо [15, 17].

Відповідно до мети застосування, завдання для формування вмінь учнів розв'язувати текстові задачі поділяють на підготовчі, навчальні і перевірні [65, 23]. Мета підготовчих завдань – активізувати опорні знання й уміння, необхідні для розв'язування задач. Вони використовуються або на початку уроку, або безпосередньо перед розв'язуванням задачі. За формою подачі підготовчі завдання, в основному, усні, в окремих випадках – письмові. Зазначимо, підготовчі завдання не повинні містити труднощів, які неможливо подолати за допомогою актуалізації знань і вмінь, в основі їх – посилання на відповідний теоретичний матеріал підручника. До підготовчих відносять завдання-питання і прості текстові задачі.

Завдання-питання спрямовані на відтворення засвоєних теоретичних знань (правил, формул, математичних понять), які мають допомогти дітям при розв'язуванні задач. Наприклад: «Сформулюйте правило знаходження шляху за відомим часом і швидкістю руху».

Підготовчі текстові задачі – це задачі на 1–2 дії, способи розв'язування яких вже знайомі учням, але їх необхідно активізувати. Це обумовлюється, по-перше, тим, що вони мають входити у зміст задачі, яка розв'язуватиметься на уроці, по-друге, їх доцільно повторити для закріплення відповідного способу перекладу залежностей, заданих словесно, на математичну мову. Для вирішення даного завдання доцільно проаналізувати задачний матеріал уроку чи окремої теми, визначити основні теоретичні поняття з математики, на основі яких розв'язуватимуться задачі [12, 41].

Основна мета навчальних завдань – ознайомлення і засвоєння учнями способів розв'язування задач певних видів; закріплення, поглиблення і вдосконалення вмінь застосовувати набуті знання на практиці. Завдання мають відрізнятися різним рівнем складності.

Серед навчальних завдань виділяють в окрему групу пробні. Це завдання на первинне застосування набутих знань. А тому процес виконання задач проходить повільно, із збереженням усіх етапів розв'язування, на всіх рівнях уявлення (предметного, образного, схематичного, графічного та ін.). Вчені рекомендують для складання пробних завдань не застосовувати великі числові дані. Головне, при їх виконанні – первинне засвоєння учнями способу розв'язування [2, 41].

Навчальні завдання відрізняються від пробних часом їх пропонування учням: для виконання пробних завдань необхідно використати знання, актуалізовані на даному уроці, для навчальних – необхідно ці знання пригадати самостійно, вичленити із вже засвоєних раніше. Крім того, навчальні завдання відрізняються більшим ступенем самостійності, різноманітністю форм і сюжетів, рівнем складності; їх розв'язування потребує від учнів продуктивних і творчих дій.

Перевірні завдання відрізняються від навчальних лише метою їх застосування – перевірити, як учні вміють розв'язувати текстові задачі певних видів, як в них сформувалися часткові вміння виконувати окремі, дії. А тому перевірні завдання можуть бути повні і фрагментарні [19, 26].

За формою побудови завдання можуть бути стандартними і нестандартними. Стандартні завдання – це задачі, в яких присутні всі складові елементи. Вони призначені для засвоєння і закріплення вмінь розв'язувати задачі певних видів. Стандартні завдання містять достатню кількість даних для отримання однозначного розв'язку і при цьому зайві дані відсутні; у їх змісті немає суперечності; завдання відповідають реальності Це означає, що питання тісно пов'язані із даними, умова достатньо точно висловлена і завдання піддається математизації.

Нестандартні завдання спрямовані на практичне застосування набутих раніше учнями знань і вмінь у змінених, незвичайних умовах, на розширення, поглиблення й удосконалення вмінь завдяки різноманітним варіантам постановки завдань. У завданнях даного типу присутні нешаблонні ситуації, що потребують застосування пошукового досвіду, здогадки, кмітливості, проведення складних порівняно зі стандартними задачами міркувань, певних напружень розумової діяльності і творчого підходу. Найчастіше в методичній літературі нестандартні завдання називають творчими [14, 4].

До нестандартних відносять завдання із зайвими даними; недостатніми даними; суперечливими даними; неправильним або незвично сформульованим текстом. Крім того, до нестандартних належать завдання на складання або переформулювання задач. Ці завдання відзначаються тим, що в першому випадку на їх основі необхідно скласти нову задачу, а в другому – основою для складання нової задачі є вже розв'язана або подана готова.

Отже, текстові задачі спрямовані на вдосконалення і поглиблення математичних знань, формування математичних умінь, розвиток творчого і логічного мислення. Вони передбачають поступове ускладнення і достатню кількість завдань для кожної групи учнів і, залежно від рівня навчальної діяльності, виконуються під керівництвом учителя, напівсамостійно чи самостійно.

1.2 Місце задач на рух у системі складених задач

У підручниках для початкових класів є такі задачі, які традиційно називають типовими. До типових належать задачі на знаходження четвертого пропорційного (на спосіб прямого і оберненого зведення до одиниці та спосіб відношень), пропорційне ділення, на знаходження числа за двома різницями, на знаходження середнього арифметичного. Методика розв'язування типових задач принципово не відрізняється від розгляду будь-яких інших задач нового виду, тобто включає підготовку, ознайомлення і розвиток умінь. Проте деякі особливості роботи над типовими задачами необхідно враховувати.

Розв'язування типових задач, пов'язаних з пропорційними величинами, ґрунтується на знанні відповідних зв'язків між величинами. Ознайомлення з величинами проводиться одночасно з розкриттям зв'язків між ними. Зв'язки формулюють у вигляді висновків. Наприклад, якщо відомо швидкість і час, то відстань можна знайти дією множення [20, 51]. Типові задачі мають деякі характерні ознаки, які враховуються на підготовчому етапі роботи. Слід також мати на увазі взаємозв'язки між окремими типовими задачами.

У початкових класах виділяють ще задачі з певним конкретним сюжетом. Це задачі на зустрічний рух, на час, задачі з геометричним змістом. Розглянемо задачі на рух.

Розв'язуванню задач на зустрічний рух передує тривала робота з розв'язування простих та складених задач на знаходження швидкості, часу та відстані. Поняття швидкості вводять на основі життєвого досвіду дітей та безпосередніх практичних дій.

Підготовча робота до розв'язування задач, пов'язаних з рухом, передбачає узагальнення уявлень дітей про рух; ознайомлення з новою величиною – швидкістю, розкриття зв'язків між величинами: швидкість, час, відстань [46, 17].

Під час ознайомлення із швидкістю доцільно так організувати роботу, щоб учні визначили швидкість свого руху пішки. Для цього в дворі, в спортзалі або коридорі можна позначити «замкнуту доріжку», поділивши її на відстані по 10 м, щоб зручніше було визначати шлях, який проходить кожний учень. Учитель пропонує дітям іти доріжкою, наприклад, протягом 4 хв. Учні самостійно легко знайдуть, користуючись десятиметровими позначками, пройдену відстань. На уроці кожен учень може обчислити, яку відстань він проходить за 1 хв. Учитель повідомляє, що відстань, яку пройшов учень за хвилину, називають його швидкістю. Учні називають свої швидкості. Потім учитель називає швидкості деяких видів транспорту. Ці дані учні можуть записати в своїх довідниках і потім використати під час складання задач.

Для формування навичок корисно усно розв'язувати задачі за таблицями. Наводимо зразки таблиць [45, 42].

1) Знайти швидкість

2) Знайти відстань

3) Знайти час

4) Знайти невідомі величини

Для узагальнення уявлень дітей про рух корисно провести спеціальну екскурсію для спостереження за рухом транспорту, після чого організувати спостереження в умовах класу, де рух демонструватимуть самі діти. На екскурсії під час роботи в класі простежити за рухом одного тіла і двох тіл одне відносно одного. Так, одне тіло (трамвай, машина, людина тощо) може рухатися швидше і повільніше, може зупинитися, може рухатися по прямій або кривій. Два тіла можуть рухатися назустріч одне одному, і при цьому вони зближуються, можуть рухатися в протилежних напрямах, віддаляючись одне від другого, а можуть рухатися в одному напрямі. Спостерігаючи такі ситуації в умовах класу, треба показати дітям, як будують креслення: відстань позначають відрізком; місце (пункт) відправлення, зустрічі, прибуття тощо позначають або точкою на відрізку і відповідною буквою, або рискою, або прапорцем; напрям руху позначають стрілкою.

Зв'язки між величинами: швидкість, час, відстань – розкривають за такою самою методикою, як і зв'язки між іншими пропорційними величинами. Внаслідок цієї роботи діти повинні засвоїти такі зв'язки: якщо відомі відстань і час руху, то можна знайти швидкість дією ділення; якщо відомі швидкість і час руху, то можна знайти відстань дією множення. Якщо відомі відстань і швидкість, то можна знайти час руху дією ділення [65, 23].

Далі, спираючись на ці знання, діти розв'язуватимуть складені задачі, у тому числі задачі на знаходження четвертого пропорційного, на пропорційне ділення, на знаходження невідомих за двома різницями з величинами: швидкість, час, відстань. Під час роботи над цими задачами треба частіше використовувати ілюстрації у вигляді креслення, бо креслення допомагає правильно уявити життєву ситуацію, відбиту в задачі. Як і в процесі розв'язування задач інших видів, треба пропонувати вправи творчого характеру на перетворення і складання задач.

Під час роботи над задачами на рух можна виділити такі основні поняття, без усвідомлення яких неможливе їх правильне розв'язування.

1. Зустрічний рух:

– швидкість зближення;

– час руху до зустрічі (час зближення), якщо два тіла одночасно (неодночасно) почали рухатися назустріч одне одному з однаковими (неоднаковими) швидкостями.

2. Рух у протилежних напрямках:

– швидкість віддалення;

– час віддалення, якщо два тіла почали одночасно (неодночасно) рухатися з одного пункту у протилежних напрямках з однаковими (різними) швидкостями.

3. Рух в одному напрямі:

– швидкість зближення (віддалення);

– час зближення (віддалення).

4. Рух за течією чи проти течії:

– власна швидкість катера (моторного човна, тощо);

– швидкість катера за течією;

– швидкість катера проти течії;

– швидкість зближення і час зближення, коли катер наздоганяє пліт;

– швидкість зближення і час зближення, коли катер рухається назустріч плоту;

– швидкість віддалення і час віддалення, коли катер і пліт рухаються з одного пункту у протилежних напрямках.

5. Середня швидкість руху:

– середня арифметична величина;

– середня швидкість як середня арифметична величина [41, 25–26].

Після виконання вправ з підручника учні зможуть порівняти швидкості живих істот та різних видів транспорту, зробити чіткі висновки про залежність між величинами: швидкість, час і відстань. Щоб краще школярі розуміли і запам'ятовували, як знайти одну з величин, коли відомі дві інші, сприятиме така схема:

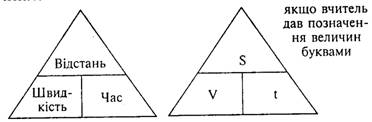
Однак необхідно періодично вимагати від школярів пояснення: чому, щоб знайти час, треба відстань поділити на швидкість; чому, щоб знайти…

Саме при розв'язуванні простих задач, пов'язаних з цими величинами, прийоми складання обернених задач та зміни числових даних певним чином допомагають ознайомити учнів з пропорційною залежністю між величинами.

Спочатку корисно складати і розв'язувати тріади простих взаємно обернених задач, записуючи їх умови в таку таблицю:

Потім вчителю слід продемонструвати учням, що станеться, якщо одну з величин зафіксувати (не змінювати), а другу збільшити чи зменшити в кілька разів. Умови задач, що порівнюються, записуються одній таблиці.

Корисно також за готовими таблицями складати і розв'язувати задачі усно, а потім проводити бесіди з учнями, порівнюючи умови та відповіді задач [5, 52].

За таблицею можна провести таку бесіду [41, 26]:

– Чим схожі задачі 1) і 2)? (Час однаковий).

– Чим вони різняться? (Швидкість збільшилась удвічі у задачі 2).

– Порівняйте відповіді, як змінилася відстань? (Відстань збільшилась удвічі).

– Чому так сталося? (Тому, що за кожну годину машина проїжджає більшу відстань).

– Порівняйте задачі 3) і 4). Чим вони схожі? (Однаковий час).

– Чим різняться задачі 3) і 4)? (Відстань зменшилася удвічі в задачі 4).

– Порівняйте відповіді задач. Що сталося зі швидкістю, коли відстань зменшилася удвічі, а час не змінився? (Швидкість теж зменшилася удвічі).

– Чим схожі задачі 1) і 5)? (Швидкості однакові).

– Чим різняться задачі 1) і 5)? (Час у задачі 5) більший удвічі).

– Порівняйте відповіді задач 1) і 5). Як змінилася відстань, коли час удвічі збільшився при тій самій швидкості? (Відстань збільшилася удвічі).

– Чому так сталося? (Тому, що чим довше їде машина, тим більшу відстань проїжджає).

– Чим схожі і чим різняться задачі 7) та 6)? (Відстані однакові, а швидкість збільшилася удвічі).

– Як змінився час? (Зменшився удвічі).

– Як це можна пояснити? (У задачі 6) за кожну годину машина проїжджала 30 км від усієї відстані – 240 км, а у задачі 7) машина удвічі більше проїжджає за годину – 60 км, вона подолає відстань 240 км за час удвічі менший).

– Чим схожі і чим різняться задачі 8) і 9)? (Відстані однакові, а час зріс у 4 рази в задачі 9). Відповіді різні. Швидкість у задачі 9) у 4 рази зменшилася).

– Чому швидкість зменшилася у 4 рази у задачі 9)? (Ту саму відстань 240 км машина подолала за час у 4 рази довший, тобто рухалася у 4 рази повільніше, ніж у задачі 8).

– Чим схожі та чим різняться задачі 10) та 11)? (Швидкості однакові, а відстань більша у 3 рази в задачі 11).

Відповідь – час у задачі 11) зріс також у 3 рази).

– Як пояснити зміну у відповіді? (Якщо швидкість машини не змінилася, то утричі більшу відстань вона зможе подолати за утричі більший час).

Так пропедевтично учні ознайомлюються з прямо пропорційною залежністю між величинами, коли із збільшенням (зменшенням) однієї величини у кілька разів, друга величина збільшується (зменшується) у стільки ж разів, та з обернено пропорційною залежністю між величинами, коли із збільшенням (зменшенням) однієї величини у кілька разів, друга – зменшується (збільшується) у стільки ж разів.

Перед розв'язуванням задач на рух назустріч, в одному напрямку та у протилежних напрямках, корисно нагадати учням завдання з підручника, де потрібно за малюнками знайти, на скільки наближаються чи віддаляються тварини одна від одної за 1 с; за 1 хв. Потім, показуючи малюнки тварин або моделі машин, чи викликавши двох учнів до дошки, учитель демонструє зустрічний рух тіл, або рух у протилежних напрямках, в одному напрямку.

Доцільно запитати у школярів, які дозволені швидкості машин у межах міста; чи може «Таврія» наздогнати «Ладу»; коли швидше віддаляється автомобіль від автобуса, якщо вони починають рухатися з одного пункту в одному напрямку чи в різних, чому так… Проводячи бесіди про безпеку руху, вчитель запрошує батьків-водіїв, щоб вони розповіли дітям про різні випадки зі свого досвіду, як слід враховувати безпечні швидкості машин під час ожеледиці, мряки тощо [15, 19].

На уроках математики вчитель, використовуючи машини-іграшки, підводить дітей до висновку, що коли машини одночасно починають рухатися з одного пункту в протилежних напрямках, то сума їх швидкостей буде швидкістю віддалення. Якщо ж машини рухаються по прямому шляху назустріч, то сума їх швидкостей буде швидкістю зближення.

Після складання відповідних задач вчитель одразу має пояснити, як записувати умову у вигляді графічної схеми, як можна розв'язати задачі двома способами, виявити з учнями більш раціональний спосіб. За задачами проводяться бесіди [24, 78].

Подібні бесіди необхідні також під час першого ознайомлення із задачами на рух у протилежних напрямках та в одному напрямку. Надалі учні зможуть розв'язувати задачі самі з неповним аналізом, називаючи лише те, що потрібно знайти для відповіді на запитання задачі.

Корисно, щоб учитель привчив дітей робити схеми аналітичного або синтетичного способу розбору задач, хоча це не належить до обов'язкових умінь, наведених у програмі з математики для 1–4 класів.

2. Формування умінь учнів розв’язувати задачі на рух

2.1 Аналіз системи задач на рух у початковому курсі математики

Вивчення всіх питань програми з математики пов'язане з розв'язуванням арифметичних задач. З одного боку, вони є важливим засобом формування в учнів математичних понять, запобігаючи формалізму у їх засвоєнні, а з другого боку, посилюють розвивальний ефект вивчення математики, впливаючи на розвиток математичного мислення учнів і їх оволодіння загальними прийомами міркування.

Через задачі передбачається засвоєння елементів арифметичної теорії; зміст арифметичних дій, властивості арифметичних дій взаємозв'язок між результатом і компонентами арифметичних дій, кількісні відношення між числами. За допомогою задач формується уявлення про величини, їх одиниці зв'язок між величинами. Окремою групою виступають задачі з величинами: ціна, кількість, вартість; час, швидкість, відстань; довжина, ширина, площа. Ці задачі сприяють усвідомленню пропорційної залежності між величинами, розширюють пізнавальний досвід дітей, допомагають застосовувати здобуті знання в практичній діяльності [20, 51].

Формування навичок розв’язувати задачі зводиться до планомірного і систематичного опрацювання тих окремих умінь, з яких складається загальне уміння – розв'язувати задачу. Тут передбачено формування вмінь слухати задачу, повторити її детально або своїми словами, визначити відомі і невідомі величини, проаналізувати зміст задачі, зобразити задачу у вигляді малюнка, схеми, правильно здійснити вибір дії для розв'язування задачі та обґрунтувати її, розв'язати задачу, зробивши відповідні записи, перевірити правильність розв'язання.

Також у процесі розв’язування задачі формуються уміння учнів правильно міркувати, висловлювати обґрунтовані судження під час розв'язання задачі і вибору відповідної дії розв'язання. Поряд із розв'язуванням готових задач передбачено навчання учнів складати задачі (за малюнком, за виразом, за коротким записом, за таблицею, за схемою, тощо).

Добір і розподіл задач за класами у програмі з математики здійснено з урахуванням доступності та доцільності для оволодіння математичним змістом. У програмі розроблено відповідні вимоги до кінцевих навчальних результатів згідно з визначеними основними функціями задач.

Відповідно до програми, розробленої Л.І. Кочиною та Н. Листопад [28], у 4 класі учні вивчають складені задачі на 2–4 дії, удосконалюють загальні прийоми розв'язування задач. При цьому учень розв'язує прості задачі на знаходження швидкості руху, відстані, часу; розв'язує задачі на знаходження середнього арифметичного; розв'язує задачі на пропорційне ділення; розв'язує задачі на знаходження невідомого за двома різницями; розв'язує задачі на 2–4 дії, що по-різному скомбіновані із простих задач вивчених видів; уміє складати план розв'язування складеної задачі; записує розв'язання задачі з поясненням і без пояснення; складає задачі за даним рівнянням і виразом; складає вирази для розв'язування задач з буквеними даними. Всі ці етапи та особливості стосуються і розв’язування задач на рух.

У школярів середніх та старших класів виникають чималі труднощі під час розв'язування задач на рух. Однією з причин цього ми вважаємо недостатню сформованість у початкових класах понять про величини: час, відстань, швидкість та пропорційну їх залежність. У молодших школярів необхідні поняття можливо формувати як на матеріалі чинних підручників початкових класів, так і доповнюючи його задачами, складеними на підґрунті типових задач, призначених для учнів середніх класів.

Оскільки предметом дослідження в цій роботі є задачі на рух, то розглянемо, як на практиці використовуються такі задачі вчителями початкових класів. Як відомо, задачі на рух запроваджуються у 4 класі. Вчителі початкових класів, знаючи методику роботи над задачами на рух, далеко не завжди можуть досягнути позитивних результатів у практиці своєї роботи. Причин, які пояснюють даний факт, є декілька.

Вивчаючи це питання, ми провели опитування у школах Тернопільської області. Шляхом спостереження, анкетування, бесід з учителями та учнями ми намагалися з’ясувати стан використання задач на рух в початковій школі, дослідити можливості їх впливу на розвиток учнів, з’ясувати питання готовності вчителів і учнів працювати з такими задачами і причини, що цьому заважають.

Нас цікавили питання:

1)   чи вважають учителі доцільним розв’язування задач на рух;

2)   чи вважають вони достатньою кількість таких задач, що подані у підручнику для 4 класу;

3)   чи відчувають учителі труднощі у розв’язуванні і поясненні учням задач на рух;

4)   в якій формі (індивідуальній, фронтальній) організовують роботу з цими задачами;

5)   які методи застосовують під час роботи;

6)   чи надають допомогу на уроці учням, які виконують завдання самостійно;

7)   яка категорія дітей працює самостійно над задачами на рух;

8)   яке значення мають такі задачі для учнів початкової школи.

Результати анкетування показали, що фактично усі вчителі початкових класів вважають доцільним і навіть необхідним розв’язування задач на рух (і надають їм великого значення). Адже, на думку вчителів, такі задачі будуть високоефективними у перспективі, оскільки вміння розв’язувати задачі на рух є необхідною умовою особистісного та суспільного розвитку людини.

Основна маса опитаних учителів вважає, що у підручнику з математики для 4 класу кількість задач на рух є недостатньою для досягнення бажаних результатів. Не досить досвідчені учителі відчувають деякі труднощі при поясненні учням особливостей задач на рух. Класоводи надають допомогу учням, які виконують завдання самостійно, а це означає, що недостатньо проведено роботи над задачами або використана досить мала кількість вправ і завдань, і, нарешті, через незнання методики роботи над задачами на рух.

Таким чином, проведений аналіз засвідчує, що в практиці початкової школи проблема використання задач на рух має певні відображення. В роботі над цими задачами і вчителі, і учні відчувають труднощі і потребують методичної допомоги.

Особливий тип задач, які містять опис процесу руху двох тіл, що переміщуються в одному чи різних напрямках, називають задачами на рух. Ці задачі вводяться для опрацювання у 4 класі.

У підручнику з математики для 4 класу спочатку вводяться прості задачі на рух, далі – складені, і нарешті – задачі з типовим конкретним сюжетом: 1) задачі на зустрічний рух; 2) задачі на рух у протилежних напрямках; 3) задачі на рух в одному напрямку. Вивчення задач цього виду є засобом формування у молодших школярів поняття руху, його різновидів та напрямків, а також понять «швидкість», «час» і «відстань». Розв'язуванню задач на рух передує тривала робота з розв'язування простих та складених задач на знаходження швидкості, часу та відстані.

У підручнику з математики для 4 класу (Богданович М.В. Математика: Підручник для 4 кл. чотириріч. поч. шк. – К.: Освіта, 1994. – 226 с.) виділяють такі види задач на рух:

1) задачі на знаходження відстані (№№389, 390, 391, 392, 395, 397, 401, 407, 413, 425, 436, 444, 461, 721);

2) на знаходження швидкості (№№381, 382, 383, 384, 385, 387, 388, 402, 426, 470, 478, 486, 575, 628, 980);

3) на знаходження часу (№№398, 399, 400, 531, 768, 786, 825, 862, 868);

Серед задач на рух у протилежних напрямках виділяють задачі на знаходження відстані (№513), швидкості (№692) і часу (№782).

Серед задач на зустрічний рух виділяють задачі на знаходження відстані (№№605, 606, 609, 615, 752, 930), швидкості (№622) і часу (№№618, 624, 638, 852, 853, 975).

У програмі з математики (авт. Кочина Л.П., Листопад Н.П.) посилання на задачі на рух відсутні, проте ці задачі широко представлені в авторському підручнику. У підручнику з математики для 4 класу (Кочина Л.П., Листопад Н.П. Математика, 4 клас – К.: Літера ЛТД, 2004. – 176 с.) виділяють такі види задач на рух:

1) задачі на знаходження відстані (у розділі 3 – №№33, 34, 103, 109, 141; у розділі 4 – №№37 (1), 272, 284, 285, 287, 297, 298, 300, 313, 314, 316, 324, 329, 334, 340, 341, 379, 388 (1, 2), 394, 395, 408, 409, 415 (2), 422, 523, 549, 580);

2) на знаходження швидкості (у розділі 4 – №№289, 290, 291, 299, 313, 315, 325, 423, 430, 515, 526, 534);

3) на знаходження часу (у розділі 4 – №№286, 307, 308, 309, 313, 388 (2), 403, 584);

У вказаному підручнику, у розділі 4 окремо виділено підрозділ «Швидкість. Час. Відстань», де зосереджена основна кількість задач на рух (№№285–291).

Серед задач на рух у протилежних напрямках виділяють задачі на знаходження відстані (у розділі 4 – №422 (2)), швидкості (у розділі 4 – №423, 430, 515 (2)), проте зовсім нема задач на знаходження часу.

Серед задач на зустрічний рух виділяють задачі на знаходження відстані (у розділі 4 – №№324, 329 (1), 334, 340, 341, 379, 387, 422 (1), 523), швидкості (у розділі 4 – №329 (2, 3), 515 (1)), і також зовсім нема задач на знаходження часу.

На нашу думку, система задач на рух в обох підручниках з математики для 4 класу не є бездоганною. В чинному підручнику з математик (авт. Л. Кочина) спостерігається диспропорційність у кількості задач на рух в одному і протилежних напрямках (останніх значно менше).

У підручнику з математики (авт. М. Богданович) простих задач і задач на дві дії достатня кількість. Задач на рух у протилежних напрямках теж досить. А задач на рух в одному напрямку є лише одна, та ще й з трьома запитаннями. Тому, на нашу думку, не варто було включати в систему задач на рух задачу цього виду. Слід було б запропонувати або достатню кількість задач на рух в одному напрямку (коли два рухомі об’єкти вирушили одночасно з різними швидкостями, або коли один рухомий об’єкт наздоганяє іншого). І варто було б розглянути всі взаємообернені задачі цього виду (задачі, де невідома відстань; невідома одна з швидкостей; невідомий час руху до зустрічі). З метою усунення даних недоліків ми доповнили систему задач на рух задачами з інших джерел (див. параграф 2.3).

Аналіз навчальних програм та підручників з математики дає змогу стверджувати, що під час роботи над задачами на рух в учнів формуються такі основні поняття: зустрічний рух (швидкість зближення, час зближення); рух у протилежних напрямках (швидкість віддалення, час віддалення); рух в одному напрямі (швидкість зближення (віддалення), час зближення (віддалення); рух за течією чи проти течії (власна швидкість плавзасобу, швидкість плавзасобу за течією, швидкість плавзасобу проти течії, швидкість зближення і час зближення, швидкість віддалення і час віддалення); середня швидкість руху.

2.2 Методика розв’язування задач на рух

Навчання учнів математики на уроці організовують у формі колективної фронтальної або індивідуальної самостійної роботи, застосовують також і групову форму навчання. Колективна форма роботи має характер бесіди вчителя й учнів з елементами зв'язного пояснення. В роботі над конкретним математичним матеріалом бесіда використовується на різних етапах його опрацювання.

Особливою формою фронтальної роботи є така, коли учитель сам ставить запитання і сам відповідає на них (за суттю це метод зв'язного викладу, розповіді). Застосування такої форми в початкових класах доцільне, оскільки молодші школярі великою мірою у навчанні наслідують учителя. Коментоване розв'язування завдань учителем призначене найчастіше не для ознайомлення з новим матеріалом, а для подання учням зразків міркування.

У практиці навчання є багато ситуацій, коли необхідно, щоб ту саму задачу діти розв'язали одночасно із записом його розв'язання на дошці. Це напівсамостійна робота: один з учнів розв'язує завдання на дошці або коментує розв'язання з місця, а решта розв'язує його в зошитах. Звичайно, вчитель рекомендує дітям працювати самостійно, але учень у будь-який час може побачити запис розв'язання чи почути пояснення ходу розв'язування і звірити його зі своїм [20, 53].

Напівсамостійна форма роботи може бути застосована:

а) у процесі первинного закріплення, тобто під час розв'язування перших після показу вчителем задач на ознайомлення з новими поняттями чи новими видами задач;

б) під час розв'язування задач підвищеної складності;

в) для порівняння різних способів розв'язування того самого завдання;

г) для аналізу помилок, допущених учнями під час самостійного розв'язування завдань;

д) у ході підготовки дітей до сприймання нового матеріалу, в тому числі задач нового виду [26, 21].

Індивідуальна самостійна робота передбачає розв'язування задачі кожним учнем окремо. Вона застосовується на будь-якому з етапів навчання, але найчастіше в процесі розвитку вмінь виконувати завдання того чи іншого виду. Самостійне розв'язування задач у початкових класах майже завжди для учнів є творчим процесом.

Отже, в організації такої роботи слід враховувати вимоги щодо проблемного навчання. Вчитель спрямовує дітей на самостійне розв'язування задач за допомогою відповідних підготовчих вправ або засобів унаочнення, своєчасно виявляє помилкові міркування учнів у процесі розв'язування завдань і допомагає їм, підтримує при цьому емоційний тонус і впевненість у тому, що кожен з учнів спроможний самостійно розв'язати завдання.

В організації діяльності учнів щодо розв'язування тієї чи іншої задачі вчитель завжди ставить певну мету і залежно від неї визначає форму роботи. Зрозуміло, що колективна й індивідуальна форми роботи можуть змінюватись навіть у процесі виконання одного завдання. Наприклад, ознайомлення зі змістом задачі було проведено у формі колективної фронтальної роботи, а аналіз задачі, складання плану і її розв'язування вчитель пропонує здійснити самостійно [12, 73].

Практикуються також групові форми навчання. Здебільшого це парні, ланкові або диференційовано-групові. У початкових класах найчастіше використовують диференційовано-групову форму, що передбачає організацію роботи груп з різними навчальними можливостями. Найчастіше учнів поділяють на три групи: сильнішу, середню і слабку. За диференційовано-груповою формою навчання всі діти здебільшого працюють за завданнями, що мають спільну пізнавальну мету. Дія різних за навчальними можливостями груп учнів завдання відрізняються за обсягом, рівнем складності, мірою допомоги.

Під час ознайомлення, наприклад, з новою задачею, застосовують два способи диференціації. За першим способом диференційовану роботу організовують у комплексі з фронтальною. Ознайомлення зі змістом нової задачі проводиться фронтально. Наявність різних груп учнів учитель враховує під час первинного закріплення матеріалу. Діти першої і другої груп працюють самостійно за картками або з підручником. З учнями третьої групи вчитель повторно аналізує задачі, розглядає окремі питання, в яких висвітлюється суть задачі, її новизна [2, 44].

За другим способом учням першої групи надається можливість спробувати самостійно розв'язати задачу нового типу. Вчитель повідомляє мету роботи. Потім роздає їм картки з текстами задач нового виду, а з учнями другої і третьої груп працює над задачами фронтально.

Організовуючи самостійну роботу учнів, найчастіше застосовують такі три види диференціації: індивідуалізацію вимог до спільного завдання; надання допомоги в одному з варіантів самостійної роботи (індивідуальна допомога); спрощення одного з двох варіантів самостійної роботи.

При використанні індивідуалізації вимог до спільного завдання для всіх учнів учитель записує на дошці або вказує в підручнику одне й те саме завдання, але інструкція його виконання передбачає й деякі прийоми диференціації [15, 19–20].

Коли застосовується індивідуалізація вимог до розв'язання задач, то усім учням пропонується, наприклад, та сама задача, причому одразу подається й додаткове завдання щодо цієї задачі. Такими додатковими завданнями можуть бути: розв'язати задачу іншим способом; скласти вира; за розв'язанням задачі окремими діями; змінити запитання й знайти на нього відповідь, скласти подібну задачу: скласти і розв'язати обернену задачу, записати план розв'язування задачі та ін.

Якщо учням пропонується вправа, наприклад на обчислення виразів, то додатковими завданнями можуть бути: знайти значення виразу іншим способом, всіма можливими способами; записати подібний вираз і обчислити його значення; обчислити значення виразів і записати їх значення в зростаючому (спадному) порядку та ін.

При використанні постановки кількох запитань до умови задачі вчитель записує на дошці умову задачі і до неї 2–3 запитання. Кожен учень знаходить відповідь на стільки запитань, на скільки зможе. Зрозуміло, що бажано відповісти на всі запитання [2, 43].

За умови, що використовується додаткове завдання, не пов'язане з основним, учитель зазначає: «Учням, які першими розв'яжуть завдання, треба спробувати виконати ще й додаткове». Ним може бути: обчислення виразів, розв'язування нової задачі. а найчастіше – завдання з логічним навантаженням. Робота над додатковим завданням припиняється одразу, як тілам вчитель організує учнів на інший вид діяльності. Дітям, які не встигли чи не змогли виконати додаткове завдання, пропонується подумати над ним вдома. Невиконання його не впливає на оцінку роботи молодшого школяра.

У випадку використання індивідуальної допомоги завдання для самостійної роботи пропонується у кількох варіантах. В одному чи двох з них міститься додаткова інформація. розрахована на допомогу в розв'язуванні задач. Реалізується цей вил диференціації найчастіше через індивідуальні картки. Розгляньмо прийоми допомоги [5].

Для конкретизації задачі до задачі додається малюнок або її короткий запис. При цьому слід прочитати задачу, розглянути до неї малюнок і обґрунтувати дію, якою вона розв'язується. Розв'язання записати в зошит.

При повідомленні відповіді до задачі або числових значень виразів, коли розв'язують задачу на 2–3 дії або знаходять значення виразу, то знання відповіді допомагає аналізувати хід роботи. Знаючи відповідь, учень самостійно виправляє допущену помилку.

Використовуючи навідні вказівки чи запитання, слід мати на увазі, що вказівки безпосередньо пов'язані з конкретним змістом задач, але взагалі вони бувають на зразок таких: це задача на три дії; для розв'язання задачі буде потрібно виконати дію віднімання, а потім дію множення; подумай, як знайти ціну за вартістю і кількістю товару; будь уважний: блокнотів купили стільки, скільки зошитів; якою дією дізнаємось, у скільки разів одне число більше від іншого?

За умови використання такого виду допомоги учням, як початок розв'язування задачі, у картці подається виконання першої дії або початок аналізу числових даних і запитання для першої дії.

Також вчителі використовують подання схеми розв'язування чи графічного зображення результату аналізу задачі [65, 23]. Користуючись схемою, учням слід розв'язати задачу, склавши вираз. Використовується й подання інформації, потрібної для розв'язування завдання. Такою інформацією є правила, тлумачення залежностей між величинами та ін. Наприклад: а) щоб знайти невідоме зменшуване, до різниці слід додати від'ємник; б) щоб за відомою площею прямокутника і його довжиною знайти ширину, треба площу поділити на довжину; в) щоб скласти обернену задачу, потрібно одне з даних (яке саме?) вважати невідомим.

Наприклад, після колективного розбору умови, змісту і скороченого запису ми пропонували дітям наступне:

– Підніміть руку, хто може цю задачу розв’язати самостійно? (Сильніші учні).

– Підніміть руку, хто буде працювати над розв’язанням задачі разом зі мною? (Середні і слабкі учні).

Після розбору задачі від числових даних ми пропонували школярам:

– Хто вже виконав розв’язання задачі, розв’яжіть задачу другим способом. (Для сильніших учнів, при умові, що існує другий спосіб розв’язування задачі).

Зі слабшими учнями ми працювали індивідуально, стежили за записами і пояснювали незрозуміле додатково.

Після розв’язання задачі ми запитували одного із середніх учнів, яку відповідь одержали.

Далі сильніший учень зачитував розв’язання задачі другим способом із поясненням [62, 41].

Наведені прийоми допомоги, полегшення чи ускладнення завдань за умови неодноразового застосування кожного з них забезпечать практичну основу для реалізації принципу диференційованого підходу в навчанні молодших школярів. Застосовуючи принцип диференційованого підходу, вчитель має бути тактовним, спиратися на позитивні риси характеру дитини. Не слід оперувати словами «сильні учні», «слабкі учні». Краще відзначити ступінь просування дітей в опануванні вмінь, а також самостійність, оригінальність розв'язку і т. ін.

Розглянемо методику роботи з молодшими школярами над системою задач на рух [41–44].

Розв'язуванню задач на зустрічний рух передувала тривала робота з розв'язування простих та складених задач на знаходження швидкості, часу та відстані. Поняття швидкості ми вводили на основі життєвого досвіду дітей та безпосередніх практичних дій. Підготовча робота до розв'язування задач, пов'язаних а рухом, передбачала узагальнення уявлень дітей про рух; ознайомлення з новою величиною – швидкістю, розкриття зв'язків між величинами: швидкість, час, відстань. Для цього ми провели спеціальну екскурсію для спостереження за рухом транспорту, після чого організували спостереження в умовах класу, де рух демонстрували самі діти.

Спостерігаючи такі ситуації в умовах класу, ми вчили дітей будувати креслення з допомогою умовних позначень: відстань позначають відрізком; місце (пункт) відправлення, зустрічі, прибуття тощо позначають або точкою на відрізку і відповідною буквою, або рискою, або прапорцем; напрям руху позначають стрілкою.

Під час ознайомлення із швидкістю учні визначали швидкість свого руху пішки. Для цього в спортзалі позначалася «замкнута доріжка», поділена на відрізки по 10 м, щоб зручніше було визначати шлях, який проходив кожний учень. Ми пропонували дітям іти доріжкою протягом 2-х хвилин. Учні, користуючись десятиметровими позначками, легко обчислювали пройдену відстань. Ми повідомляли, що відстань, яку пройшов учень за хвилину, називають його швидкістю. Учні називали швидкість свого руху. Потім ми називали швидкості деяких видів транспорту.

Зв'язки між величинами: швидкість, час, відстань – розкривалися за такою самою методикою, як і зв'язки між іншими пропорційними величинами. Внаслідок цієї роботи діти засвоювали такі зв'язки: якщо відомі відстань і час руху, то можна знайти швидкість дією ділення; якщо відомі швидкість і час руху, то можна знайти відстань дією множення. Якщо відомі відстань і швидкість, то можна знайти час руху дією ділення.

Далі, спираючись на ці знання, діти розв'язували складені задачі з величинами швидкість, час, відстань. Під час роботи над цими задачами часто використовувалися ілюстрації у вигляді креслення.

На підготовчому етапі ми виходили з важливості усвідомлення дітьми поняття «швидкість». Для цього ми пропонували учням таку систему завдань та запитань:

– Яке слово вживають водії, порівнюючи швидкість руху різних марок машин? Що ж таке швидкість, як ви гадаєте?

– Чому деякі поїзди називають швидкими, чим вони відрізняються від звичайних?

– Допоможіть хлопчикам, які посперечалися, хто з них швидше прийшов до школи:

а) Петрик пройшов 120 м за 5 хвилин, а Дмитрик – 120 м за 3 хвилини. Хто швидше йшов?

б) Микола пройшов 300 м за 6 хвилин, а Сергій – 450 м за 9 хвилин. Хто швидше йшов?

в) Антон пройшов 280 м за 7 хвилин, а Михайло – 480 м за 16 хвилин. Хто швидше йшов?

Підготовча робота даного змісту готувала молодших школярів до розв’язування складених задач на рух. Розглянемо методику роботи над задачами на рух у зустрічному напрямку.

Задача 1. З пристані Київ до пристані Кременчук вийшов теплохід, і одночасно йому назустріч з пристані Кременчук вийшов катер. Теплохід ішов зі швидкістю 30 км/год, а катер – 24 км/год. Через 5 год вони зустрілися. Яка відстань між пристанями? Під час повторення змісту задачі вчитель креслить на дошці ілюстрацію:

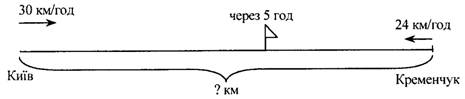
Бесіда. Що означає: «Через 5 год вони зустрілися»? (Теплохід і катер з моменту виходу до моменту зустрічі були в дорозі 5 год.) Яку відстань пройшов за 5 год теплохід? («Від пристані Київ до прапорця», – показує один учень біля дошки.) Яку відстань пройшов катер за 5 год? (Другий учень показує на кресленні.) То з яких двох частин складається шукана відстань між пристанями? (З відстаней, які пройшов кожен теплохід за 5 год.) Чи можемо ми взнати відстань, яку пройшов теплохід до зустрічі? (Можемо, бо відомо його швидкість і час руху до зустрічі.) Чи можемо взнати відстань, яку пройшов до зустрічі катер? (Можемо.)

А коли обидві відстані будуть відомі, про що зможемо дізнатися? (Про відстань між пристанями.) Давайте запишемо розв'язання виразом. Що знайдемо в першій дії? Якою дією? (Вчитель пише на дошці, а учні в зошитах: 30 • 5.) Про що дізнаємося в другій дії? Якою дією? Поруч з'являється другий запис: 30 • 5; 24 • 5. Про що дізнаємося в третій дії? Чого бракує, щоб скласти остаточний вираз? (Вписують знак «+»: 30 • 5 + 24 • 5.) Чи потрібні дужки? Учні усно обчислюють проміжні результати. Записи мають вигляд: 30 • 5 + 24 • 5 = 150 + 120 = 270 (км).

Ми розв'язали задачу першим способом. Її можна розв'язати і по іншому. Чи можемо ми взнати, на скільки кілометрів наблизяться теплохід і катер один до одного за першу годину руху? (Так, 30 + 24 = = 54 км.) На яку відстань наблизяться вони за другу годину? (На 54 км.) За третю годину? Четверту? П'яту? Ви бачите, що за кожну годину вони наближаються на 54 км, а таких годин до зустрічі пройшло 5. То про що тепер можна дізнатися? (Скільки кілометрів пройшли до зустрічі теплохід і катер разом.) А це і означає, що ми знайдемо відстань між пристанями. Якою дією? Хто запише на дошці вираз? (Учень записує: (30 + 24) • 5 = 270 (км).) Ви бачите, що відповіді в обох способах вийшли однакові.

Далі вчитель ще раз аналізує другий спосіб розв'язання. Звертає увагу учнів на те, що відстань, яку проходять за кожну годину теплохід і катер разом, дорівнює сумі швидкостей і називається швидкістю зближення. Щоб обчислити відстань між пристанями, ми швидкість зближення множили на час руху до зустрічі.

Задача 2. Відстань між пунктами А і В 18 км. З пункту А у напрямку до пункту В вийшов турист, а другий турист одночасно вийшов йому назустріч з пункту В. Через який час зустрінуться туристи, якщо їхні швидкості однакові і дорівнюють 3 км/год?

Графічна ілюстрація буде опорою під час аналізу задачі. Прапорець позначає місце зустрічі.

? год

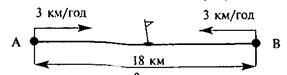
Аналіз можна провести від числових даних.

Запитання до учнів:

–   З якою швидкістю рухалися туристи?

–   Де буде місце зустрічі туристів?

– На скільки кілометрів наближаються туристи один до одного за 1 год?

–   Яка швидкість зближення?

–   Що відомо про відстань АВ?

–   Чи можна дізнатися, через який час зустрінуться туристи?

Розв'язання:

1) 3 + 3 = 6 (км/год) – швидкість зближення туристів;

2) 18: 6 = 3 (год) – час, через який зустрінуться туристи.

Відповідь. Через 3 год.

Задача 3. Відстань між пунктами А та В складає 24 км. З пункту А до пункту В вийшов турист зі швидкістю 3 км/год, а з пункту В назустріч йому через 1 год вийшов другий турист зі швидкістю 4 км/год. Через який час після виходу другого туриста відбулася їхня зустріч?

Графічна ілюстрація змісту задачі.

? год

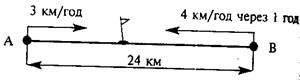
Запитання до учнів під час аналізу задачі можуть бути такими:

–   Що відомо про відстань АВ?

–   Скільки кілометрів пройшов перший турист до виходу другого?

–   Як ви це знайшли?

–   Яку відстань залишилось пройти обом туристам до зустрічі?

–   Які швидкості туристів?

–   На скільки кілометрів зближаються туристи за 1 год?

– Якщо відомі швидкість зближення і відстань, яку залишилося пройти до зустрічі, що можна знайти?

Учні складають план розв'язування задачі і записують розв'язання.

Розв'язання:

1) 3 • 1 = 3 (км) – пройшов перший турист до виходу другого;

2) 24 – 3 = 21 (км) – залишилось пройти обом до зустрічі;

3) 3 + 4 = 7 (км/год) – швидкість зближення;

3) 21: 7 = 3 (год) – час, через який після виходу другого туриста відбудеться зустріч.

Відповідь. Через 3 год.

Задача 4. Відстань між пунктами А та В складає 28 км. З пункту А до пункту В вийшов турист зі швидкістю 3 км/год, а з пункту В назустріч йому вийшов одночасно другий турист зі швидкістю 4 км/год. На якій відстані від пункту А зустрінуться туристи?

Графічна ілюстрація змісту задачі.

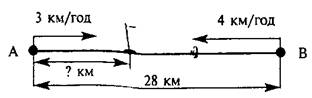
Запитання до учнів аналогічні тим, що були під час розв'язування задачі 1. Наприкінці можна запитувати:

–   Що треба знати, щоб знайти місце зустрічі?

–   Як знайти відстань від пункту А до місця зустрічі?

Крім того, можна розібрати з учнями такі питання:

–   Від чого залежить місце зустрічі?

– На якій відстані зустрілися б туристи, якщо б їхні швидкості були однакові?

–   Ближче до якого пункту станеться зустріч? Чому?

–   Що можна сказати про час руху обох туристів до місця зустрічі?

Розв'язання:

1) 3 + 4 = 7 (км/год) – швидкість зближення;

2) 28: 7 = 4 (год) – час до зустрічі;

4) 3 • 4 = 12 (км) – відстань від пункту А, на якій зустрілися туристи.

Відповідь. Через 12 км.

Після розв'язання задачі можна поставити такі запитання:

– Якими способами можна знайти відстані від місця зустрічі до пункту В?

– Як перевірити правильність розв'язання задачі?

Розглянемо методику роботи над задачами на рух у протилежних напрямках.

Задача 5. Два пішоходи вийшли з одного міста у протилежних напрямках. Перший пішохід ішов зі швидкістю 5 км/год, а другий 4 км/год. Дай відповідь на такі запитання:

1) На скільки кілометрів віддалялися пішоходи за 1 год?

2) На скільки кілометрів віддалилися пішоходи за З год?

3) Скільки кілометрів пройшов кожний пішохід за 3 год?

Вчитель ставить двох учнів посередині класу і дає кожному картку з його швидкістю. Учні стоять поряд спиною один до одного і за командою вчителя починають віддалятися один від одного. Вчитель зупиняє їх і говорить, що пройшла година. Діти з'ясовують, що пішоходи віддалилися один від одного на суму їхніх швидкостей. Учні знову починають іти і за наказом учителя зупиняються – пройшла ще одна година. Знову підраховують, на скільки кілометрів віддалилися пішоходи протягом другої години та за дві години разом.

Процедуру проробляють втретє і знову підраховують. Вчитель говорить, що кожної години пішоходи віддаляються на однакову відстань – 9 км. Тому кажуть, що 9 км/год – це швидкість їхнього віддалення. Вона, як і швидкість зближення під час зустрічного руху, дорівнює сумі швидкостей. Знаючи швидкість віддалення і час руху, можна обчислити, на якій відстані один від одного опиняться пішоходи через вказаний час. Вчитель зображує на дошці ілюстрацію:

На малюнку діти показують, з яких двох частин складається ця відстань, і обчислюють кожну частину (шляхи обох пішоходів). Один учень записує розв'язання задачі виразом на 3 дії. Після цього відстань обчислюють за допомогою швидкості віддалення і записують другий спосіб обчислення. Діти бачать, що розв'язання таке ж, як і в роботі з задачами на зустрічний рух, тільки сума швидкості має іншу назву. Вчитель пропонує уявити, що пішоходи повернулися обличчям один до одного і починають іти з тими ж швидкостями. Яку задачу тепер можна скласти? Яким буде її розв'язання? Воно повністю співпадає з розв'язанням попередньої задачі.

Задача 6. Два пішоходи рухаються у протилежних напрямках. Швидкість одного – 5 км/год, а другого – 4 км/год. На скільки кілометрів вони віддаляються один від одного за 1 год; за 2 год; за 3 год?

Графічна схема до цієї задачі:

Передумовою до розв'язання цієї задачі є попереднє з'ясування з учнями таких питань:

– У якому напрямку рухаються пішоходи, коли йдеться про швидкість зближення?

– Як знаходять швидкість зближення?

– У якому напрямку рухаються пішоходи, коли вони віддаляються один від одного?

– Як можна назвати швидкість, з якою пішоходи віддаляються один від одного?

–   Як знаходять цю швидкість?

–   Що спільного у знаходженні швидкостей зближення і віддалення?

–   Від чого залежить відстань між двома пішоходами через певний час, якщо вони вирушають одночасно?

–   Назустріч один одному?

–   У протилежних напрямках? Як знаходять відстань у цих випадках?

–   Що спільного у її знаходженні?

Запитання до учнів під час аналізу задачі:

–   Що відомо про швидкості пішоходів?

–   Яке перше запитання задачі, чи можна на нього відповісти?

Розв'язання:

1) 5 + 4 = 9 (км) – пройшли пішоходи за 1 год (швидкість віддалення);

2) 9 • 2 = 18 (км) – пройшли пішоходи за 2 год;

3) 9 • 3 = 27 (км) – пройшли пішоходи за 3 год.

Відповідь. На 9 км; на 18 км; на 27 км.

Задача 8. З пункту М вирушив пішохід зі швидкістю 5 км/год. Через 4 год з цього ж самого пункту у протилежному напрямку виїхав вершник зі швидкістю 11 км/год. Через скільки годин після виїзду вершника відстань між ним і пішоходом становитиме 68 км?

Графічна схема до цієї задачі:

Запитання до учнів під час аналізу задачі:

–   Що спільного між цією задачею і попередньою?

–   Що відомо про швидкості пішохода і вершника?

–   Скільки часу рухався пішохід, доки виїхав вершник?

– Як дізнатися, скільки кілометрів пройшов пішохід, доки виїхав вершник?

– Чи можна дізнатися, скільки кілометрів пройшли разом пішохід і вершник після виходу вершника? Як це зробити?

– Про що можна дізнатися, якщо відомі швидкості пішохода і вершника?

–   Про що запитується в задачі?

–   Які дії треба виконати, щоб відповісти на запитання задачі?

Розв'язання:

1) 5 • 4 = 20 (км) – пройшов пішохід, доки виїхав вершник;

2) 68 – 20 = 48 (км) – пройшли разом пішохід і вершник після виїзду вершника;

3) 5 + 11 = 16 (км) – пройшли разом пішохід і вершник за 1 год (швидкість віддалення);

4) 48: 16 = 3 (год) – через стільки годин після виїзду вершника відстань між ним і пішоходом становитиме 68 км.

Відповідь. Через 3 год.

Можна запропонувати школярам записати розв'язання цієї задачі у вигляді числового виразу, а також відповісти на запитання:

– Через який час після виходу пішохода відстань між ним і вершником становитиме 68 км?

Розв'язання:

1) (68 – 5 • 4): (5 + 11) = 3 (год) – через стільки годин після виходу вершника відстань між ним і пішоходом становитиме 68 км;

2) 4 + 3 = 7 (год) – через стільки годин після виходу пішохода відстань між ним і вершником становитиме 68 км.

Відповідь. Через 7 год.

Задача 9. Два літаки одночасно вилетіли з аеродрому в протилежних напрямках. Через півгодини після вильоту відстань між ними була 720 км. Перший літак летів зі швидкістю 15 км/хв. З якою швидкістю летів другий літак? Графічна схема до цієї задачі:

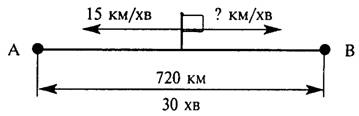
Запитання до учнів під час аналізу задачі:

–   Що відомо про рух першого літака і про що можна дізнатися?

–   Яка відстань між літаками була через півгодини після вильоту?

–   Чи можна знайти відстань, яку пролетів другий літак?

–   Про що запитується в задачі?

–   Які дії треб виконати, щоб відповісти на запитання задачі?

Розв'язання:

1) 15 • 30 = 450 (км) – пролетів перший літак;

2) 720 – 450 = 270 (км) – пролетів другий літак;

3) 270: 30=9 (км/хв) – швидкість другого літака.

Відповідь. 9 км/хв.

Розглянемо методику роботи над задачами на рух в одному напрямку.

Задача 10 (№619).

Від однієї пристані вирушили в одному напрямі катер і буксир. Швидкість катера 27 км/год, а буксира 18 км/год. Яка відстань буде між ними через 3 год? (Розв'яжи задачу двома способами.)

Ілюстрація.

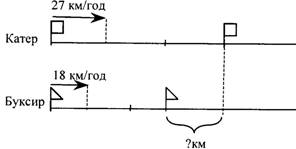
Бесіда. Хоч у задачі про це не сказано, але мається на увазі, що катер і буксир вирушили одночасно. Скільки годин був у дорозі кожен з них? (З години.) То що ми можемо взнати про рух кожного? (Відстані, які пропливли за цей час катер і буксир.) Коли будуть відомі пройдені відстані, що можна буде взнати? (Відстань між катером і буксиром.) То на скільки дій задача? (На три.) Учні записують розв'язання першим способом.

– Задача має і другий спосіб розв'язування. Уявіть собі, як рухаються катер і буксир. Лише в початковий момент руху вони перебувають поруч. А далі з першої ж хвилини катер починає випереджати буксир. Чому? (Бо його швидкість більша.) Чи можна взнати, на скільки кілометрів випередить катер буксир через 1 годину? (Можна: 27 – 18 = 9 (км).) Вчитель показує цю відстань на малюнку. Протягом другої години катер знову випередить буксир на 9 км. То яка відстань буде між катером і буксиром через 2 години? (9 + 9 = 18 (км).) А через 3 години? (18 + 9 = 27 (км).) Вчитель щоразу показує ці відстані на малюнку:

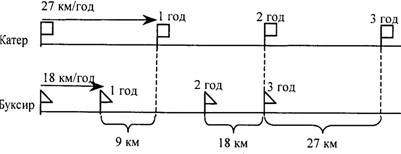
Можна підкреслити, що катер за 2 год пройшов відстань, на подолання якої буксирові знадобилося 3 год: 27 • 2 = 54 (км); 18 • 3 = 54 (км).

Тому на малюнку не випадково другий і третій прапорці на кожній прямій розміщені строго один під одним. Учні записують розв'язання другим способом:

1) 27 – 18 = 9 (км) – на стільки катер випереджає буксир за кожну годину;

2) 9 • 3 = 27 (км) – на стільки він випередить буксир через 3 години.

Відповідь. На 27 км.

Задача 10 (№693).

Від Луганська до Львова летіли літак і вертоліт. Спочатку літак був позаду вертольота на 400 км. Швидкість літака 12 км/хв, а вертольота – 2 км/хв. Яка буде між ними відстань через 20 хв? Коли літак порівняється з вертольотом? Яка відстань буде між ними через 1 год?

І спосіб.

Бесіда. Подивіться на малюнок і скажіть, який момент польоту на ньому зображено? (Початковий момент, коли між: літаком і вертольотом відстань становила 400 км.) Щоб дізнатися, яка відстань буде між літаком і вертольотом через 20 хв, давайте спочатку визначимо, де опиниться кожен з них через 20 хв. Чи можемо ми взнати, скільки кілометрів пролетить літак за 20 хв? (Так. 12 • 20 = 240 (км).)

Вчитель відмічає місцезнаходження літака прапорцем. Про що тепер можна дізнатися? (Скільки кілометрів пролетить вертоліт за 20 хвилин: 2 • 20 = 40 (км).)

Вчитель показує і цю відстань на малюнку:

Як можна тепер обчислити відстань між прапорцями? Можна дізнатися, на якій відстані від Луганська буде вертоліт. А на якій відстані від Луганська в цей момент буде літак, ми вже знаємо. То як тоді дізнаємося про відстань між літаком і вертольотом? (Від усієї відстані, яку пролетів від Луганська вертоліт, віднімемо відстань, яку пролетів літак.) При цьому вчитель усі відстані показує на малюнку. Після цього учень коментує, а решта учнів записують дії з поясненням:

1) 12 • 20 = 240 (км) – пролетів літак за 20 хв;

2) 2 • 20 = 40 (км) – пролетів вертоліт за 20 хв;

3) 400 + 40 = 440 (км) – пролетів усього вертоліт;

4) 440 – 240 = 200 (км) – буде відстань між ними через 20 хв.

Чи можна обчислити цю відстань по іншому? Подивіться на малюнок і покажіть, з яких двох частин складається відстань між прапорцями. (Один учень показує). Чи можемо ми обчислити першу частину? (Так, треба від 400 км відняти відстань, яку пролетів літак). Що зробимо після цього? (До знайденого результату додамо другу частину – 40 км.)

II спосіб.

1) 12 • 20 = 240 (км) – пролетів літак за 20 хв;

2) 400 – 240 = 160 (км) – не долетів літак до місця, в якому перебував вертоліт у початковий момент;

3) 2 • 20 = 40 (км) – пролетів вертоліт за 20 хв;

4) 160 + 40 = 200 (км) – буде відстань між ними через 20 хв.

Ви бачите, що другий спосіб не є коротшим від першого.

Але є ще один спосіб, без обчислення відстаней, які пролетіли літак і вертоліт за 20 хв. Подивіться на їхні швидкості. Як вони описують рух обох літальних апаратів? (Обидва рухаються в одному напрямі. Літак летить швидше, отже, наздоганяє вертоліт, тому відстань між ними скорочується.) Отже, найбільша відстань (400 км) була між ними у початковий момент, а далі вона почала зменшуватися, тобто літак почав наближатися до вертольота. Чи можемо ми взнати, на скільки кілометрів наблизиться літак до вертольота за 1 хв? Можемо. За 1 хв літак пролетить 12 км.

Якби вертоліт не рухався, це означало б, що літак за 1 хв наближається до вертольота на 12 км. Але вертоліт за цю ж хвилину віддаляється від літака на 2 км. Отже, в цілому, літак за хвилину наблизиться до вертольота не на 12 км, а на 12 – 2 = 10 (км). Якщо обидва рухаються в одному напрямі 20 хв, на скільки кілометрів вони зблизяться через 20 хв? (На 10 • 20 = 200 (км).) Якщо початкова відстань між ними була 400 км, а за 20 хв ця відстань зменшилась на 200 км, то про що можна дізнатися? (Яка відстань стала між літаком і вертольотом через 20 хв.)

Один учень на дошці записує третій спосіб розв'язання, коротший за попередні.

III спосіб.

1) 12 – 2 = 10 (км) – на таку відстань наближається літак до вертольота за кожну хвилину.

2) 10 • 20 = 200 (км) – на таку відстань наблизиться літак до вертольота через 20 хв;

3) 400 – 200 = 200 (км) – буде відстань між ними через 20 хв.

Ми відповіли лише на перше запитання. Тепер дізнаємося, коли літак порівняється з вертольотом. Що це означатиме? (Що обидва перебуватимуть на однаковій відстані від Луганська.) Вчитель показує на малюнку цю точку:

Літак порівняється з вертольотом, коли початкова відстань між ними 400 км скоротиться до нуля. За одну хвилину вона скорочується на 10 км. То як дізнатися, скільки хвилин триватиме це скорочення? (400: 10 = 40 (хв).) Отже, через 40 хв початкова відстань між ними зійде нанівець, тобто літак наздожене вертоліт.

Давайте перевіримо, чи дійсно через 40 хв і літак, і вертоліт перебуватимуть на однаковій відстані від Луганська. На якій відстані від Луганська буде знаходитися літак? (12 • 40 = 480 (км).) А як дізнатися, на якій відстані від Луганська перебуватиме в цей момент вертоліт? (2–40 = 80 (км) – стільки пролетить вертоліт за 40 хв; 400 + 80 = 480 (км) – на такій відстань від Луганська перебуватиме вертоліт.) Ви бачите, що відстані від Луганська однакові і у літака, і у вертольота, отже вони, у цей момент перебувають в одній точці траси. Це означає, що через 40 хв літак дійсно порівняється з вертольотом.

Залишилося дати відповідь на останнє запитання: яка відстань буде між ними через 1 год? Цю відстань можна теж обчислити довшим і коротшим шляхом. Під керівництвом учителя учні записують обидва способи.

І спосіб.

1) 2 • 60 = 120 (км) – пролетить вертоліт через 1 год;

2) 400 + 120 = 520 (км) – відлетить вертоліт від Луганська;

3) 12 • 60 = 720 (км) – пролетить літак через 1 год;

4) 720 – 520 = 200 (км) – на стільки літак випередить вертоліт. Вчитель у ході розв'язування показує ці відстані на малюнку:

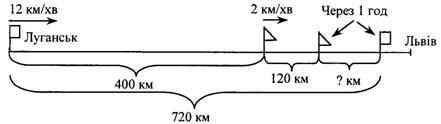
ІІ спосіб.

1) 12 – 2 = 10 (км) – на стільки наблизиться літак до вертольота за 1 хв;

2) 10 • 60 = 600 (км) – на стільки може наблизитися літак до вертольота за 60 хв;

3) 600 – 400 = 200 (км) – на стільки літак випередить вертоліт через годину.

Ви бачите, що за 1 год відстань між літаком і вертольотом може скоротитися на 600 км. Якби вертоліт у початковий момент перебував від літака на достатньо великій відстані, то так і сталося б. Але початкова відстань між ними становила лише 400 км. Тому літак може наближатися до вертольота, лише скорочуючи до нуля 400 км, а решту 200 км – почне від нього віддалятися, тобто випереджувати.

Покажемо етапи формування навичок розв’язувати задачі на рух за течією і проти течії.

Задача 11. Від пристані А одночасно вирушили вниз за течією катер і пліт. Катер спустився вниз на 96 км, далі повернув назад і повернувся до пристані А через 14 год. Знайти швидкість катера у стоячій воді і швидкість течії, якщо відомо, що катер зустрів пліт на зворотному шляху на відстані 24 км від пристані А.

На основі цієї задачі складена система задач для молодших школярів. Перед розв'язуванням їх учитель може навести аналогії «руху у стоячій воді», «руху за течією», «руху проти течії» із повсякденного довкілля, відповідно такі, як рух пішохода по тротуару, рух пасажира в автобусі від задніх до передніх дверей під час руху автобуса (рух пасажира сходинками ескалатора, що рухаються, тощо), рух пасажира у напрямку задніх дверей під час руху автобуса, потягу тощо).

Задача 13. Від пристані А одночасно вирушили вниз за течією катер і пліт. Яка відстань буде між ними через 6 год, якщо швидкість катера у стоячій воді на 12 км/год більша за швидкість течії, а швидкість течії 2 км/год?

Перед розв'язуванням цієї задачі учням слід повідомити, що швидкість катера у стоячій воді називають також власною швидкістю катера.

Після ознайомлення школярів з умовою задачі учитель має роз'яснити, що швидкість катера за течією більша за його швидкість у стоячій воді на величину швидкості течії, тобто ((12 + 2) + 2) = 16 (км/год) і що пліт і течія мають однакові швидкості (2 км /год).

При подальшому розв'язуванні задачі можна базуватися на поняттях, сформованих під час розгляду задач на «рух в одному напрямку». Доцільно звернути увагу учнів на те, що катер випереджає пліт (віддаляється від плота) на 14 км за кожну годину, що дорівнює швидкості катера у стоячій воді. Тому задачу варто розв'язати двома способами, що буде і перевіркою розв'язування. Графічна ілюстрація змісту задачі:

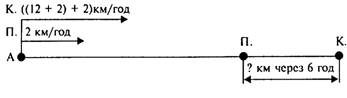
Розв'язання: 1 спосіб:

1) 12 + 2 = 14 (км/год) – швидкість катера у стоячій воді;

2) 14 + 2 = 16 (км/год) – швидкість катера за течією;

3) 16 • 6 = 96 (км) – проплив катер за 6 год;

4) 2 • 6 = 12 (км) – проплив пліт за 6 год;

5) 96 – 12 = 84 (км) – відстань між ними через 6 год.

Відповідь. 12 км.

2 спосіб:

1) 12 + 2 = 14 (км/год) – швидкість катера у стоячій воді;

2) 14 + 2 = 16 (км/год) – швидкість катера за течією;

3) 16 – 2 = 14 (км/год) – на стільки більша швидкість катера за течією, ніж плота (швидкість віддалення);

4) 14 • 6 = 84 (км) – відстань між катером і плотом через 6 год.

Відповідь. 84 км.

Задача 14. Від пристані А спускається вниз за течією пліт зі швидкістю 2 км/год, а через 7 год від пристані А у тому ж напрямку відправляється катер, який наздоганяє пліт через 1 год. Яка швидкість катера у стоячій воді?

Графічна ілюстрація змісту задачі:

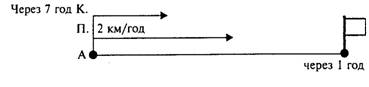
Прапорець позначає місце, де катер наздогнав пліт.

Розв'язання:

1) 7 + 1 = 8 (год) – плив пліт, доки його не наздогнав катер;

2) 2 • 8 = 16 (км) – проплив пліт за 8 год, а катер – за 1 год;

3) 16 – 2 = 14 (км/год) – власна швидкість катера (швидкість зближення катера і плота).

Відповідь. 14 км/год.

Задача 15. Від пристані А спускається вниз за течією пліт, а через 7 год від пристані А у тому ж напрямку відправляється катер зі швидкістю 16 км/год і наздоганяє пліт через 1 год. Яка швидкість течії?

Графічна ілюстрація змісту задачі:

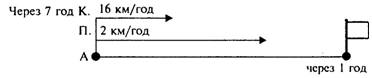
Під час аналізу задачі необхідно підвести учнів до усвідомлення можливості розв'язування її двома способами.

1 спосіб:

1) 7 + 1 =8 (год) – плив пліт, доки його не наздогнав катер;

2) 16 • 1 = 16 (км) – відстань, яку проплив катер за 1 год, а пліт – за 8 год;

3) 16: 8 = 2 (км/год) – швидкість плота або швидкість течії.

Відповідь. 2 км/год.

2 спосіб (використовувався у позакласній роботі з математики):

Припустимо, що х – швидкість течії, така ж і швидкість плота.

В основу складання рівняння покладемо відстань, яку проплив пліт до того, як його наздогнав катер. Одержимо два рівних вирази: І – 16 • 1; II – х • (7 + 1).

Складемо рівняння: 16 • 1 = х • (7 + 1), 16 = 8 • х, х = 16: 8, х = 2.

Перевірка: 2 • 8=16 (км) – проплив пліт за 8 год, а катер – за 1 год.

Відповідь: 2 км/год – швидкість течії.

Задача 12. Від пристані А спускається вниз за течією катер зі швидкістю 16 км/год на відстань 96 км і повертається назад, витративши на шлях у обидва кінці 14 год. Яка швидкість течії?

Графічна схема умови задачі:

Виходячи з того, що дану задачу учням важко розв’язати на уроці, ми використовували її у позакласній роботі з математики. Перед розв'язуванням задачі доцільно дати учням завдання скласти числовий вираз для знаходження різниці між швидкістю катера за течією і його швидкістю проти течії, якщо швидкість катера у стоячій воді – 14 км/год, а швидкість течії – 2 км/год.

(14 + 2) – (14 – 2) = 16 – 12 = 4 = 2 • 2.

Учні побачать, що швидкість катера за течією більша за його швидкість проти течії на подвійну швидкість течії.

Це саме можна зобразити за допомогою графічної схеми:

Якщо довжина відрізка АВ зображує швидкість катера у стоячій воді, а ВД – швидкість течії, тоді довжина відрізка АД буде зображати швидкість катера за течією, а АС (ВС = ВД) – швидкість катера проти течії. АД більше за АС на подвійну швидкість течії (подвійний відрізок ВД).

Далі можна перейти до розв'язування задачі, спираючись на поняття, сформовані під час розв'язування попередніх задач.

Розв'язання:

1) 96: 16 = 6 (год) – йшов катер за течією;

2) 14 – 6 = 8 (год) – йшов катер проти течії;

3) 96: 8 = 12 (км/год) – швидкість катера проти течії;

4) 16 – 12 = 4 (км/год) – на стільки більша швидкість катера за течією, ніж проти течії (подвійна швидкість течії);

5) 4: 2 = 2 (км/год) – швидкість течії.

Відповідь. 2 км/год.

Задача 13. Від пристані А одночасно у протилежних напрямках вирушають пліт і катер. Пліт спускається вниз за течією зі швидкістю 2 км/год, а катер йде проти течії. Через який час відстань між ними становитиме 84 км, якщо власна швидкість катера (у стоячій воді) – 14 км/год? Покажемо спочатку традиційне розв'язання цієї задачі.

Розв'язання:

1) 14 – 2 = 12 (км/год) – швидкість катера проти течії;

2) 12 + 2 = 14 (км/год) – швидкість віддалення;

3) 84: 14 = 6 (год) – час, за який відстань між плотом і катером становитиме 84 км.

Відповідь. 6 год.

Під час опрацювання цієї задачі можна поставити такі запитання:

– На якій відстані від пристані А знаходитимуться окремо катер і пліт і яка відстань буде між ними через 6 год? Щоб відповісти, треба знати швидкість течії.

Задача 14. Від пристані А спускається вниз за течією у напрямку до пристані В пліт. Одночасно з плотом від пристані В до пристані А вирушає катер. Відстань між А і В – 96 км, швидкість течії – 2 км/год; швидкість катера проти течії – 14 км/год. Через який час відбудеться зустріч катера з плотом.

Розв'язання:

1) 14 + 2 = 16 (км/год) – швидкість зближення;

2) 96: 16 = 6 (год) – час, через який катер зустрінеться з плотом.

Відповідь. 6 год.

Розглянемо методику розв’язування задач на знаходження середньої швидкості.

Поняття «середнє арифметичне кількох чисел» у підручнику вводиться індуктивно. Спочатку учням пропонуються задачі на знаходження середньої швидкості руху автомобіля. Вважається, що пояснення до розв'язання цих задач повинен дати вчитель. Далі розглядається розв'язання такої задачі.

Задача 15. Велосипедист одну годину їхав зі швидкістю 15 км/год, дві години – зі швидкістю 13 км/год і ще одну годину – зі швидкістю 11 км/год. З якою середньою швидкістю їхав велосипедист?

Розв'язання:

1) Скільки всього годин їхав велосипедист?

1 + 2+1 = 4 (год)

2) Скільки всього кілометрів проїхав велосипедист?

15 + 13 • 2 + 11 = 52 (км)

3) Яка середня швидкість руху велосипедиста?

52: 4 = 13 (км/год)

Розв'язання за допомогою числового виразу:

(15 + 13 • 2 + 11): (1 + 2 + 1) = 13 (км/год)

Після розв'язання цієї та попередніх задач дається загальне правило: «Щоб знайти середнє арифметичне кількох чисел, треба їх суму поділити на кількість цих чисел». Тепер вважається, що поняття «середнє арифметичне кількох чисел» вже введене, і пропонуються задачі на знаходження середньої маси кролів, середньої врожайності картоплі і гречки, середньої швидкості поїзда,…, середньої швидкості руху коня.

Задача 16. Турист за першу годину пройшов 5 км, за другу – 4 км і за третю – 3 км. З якою постійною швидкістю мав рухатися турист, щоб за той же час пройти таку ж відстань?

Турист пройшов усього 5 + 4 + 3 кілометрів, за час 1 + 1 + 1. Складемо числовий вираз: (5 + 4 + 3): (1 + 1 + 1). Згідно з цим виразом треба відстань поділити на час. Так знаходять швидкість руху. Якщо обчислимо вираз, то у відповіді отримаємо 4 км/год. Звертаємо увагу учнів на те, що, рухаючись зі швидкістю 4 км/год, турист за 3 год пройде відстань 12 км: 4 • 3 = 12 (км).

Таким чином маємо правильну рівність: 5 + 4 + 3 = 4 – 3.

Отриману швидкість називають середньою швидкістю. Тепер можна сформулювати означення середньої швидкості: «Середньою швидкістю називають таку постійну швидкість, рухаючись з якою за той же час буде пройдена та ж відстань, що і за дійсних умов руху». Щоб знайти середню швидкість, треба усю відстань поділити на увесь час руху.

З метою формування у молодших школярів навичок розв’язування задач на рух ми пропонували їм добірку задач та методично правильно опрацьовували їх.

2.3 Організація і зміст експериментального дослідження, аналіз його ефективності

На основі аналізу психолого-педагогічної та методичної літератури, а також власних спостережень за навчально-виховним процесом у початковій школі нами виявлено, що організація розв’язування задач на рух має значні методичні недоліки, а формування в учнів навичок розв’язування задач на рух перебуває на неналежному рівні. З метою забезпечення адекватності у цьому процесі нами розроблено і впроваджено у педагогічну практику початкової ланки загальної освіти удосконалену методику розв’язування задач на рух у 4 класі, а також перевірено її ефективність.

Дипломне дослідження мало теоретико-експериментальний характер і проводилося у два етапи. На теоретичному етапі (2006–2007 навчальний рік) була визначена сфера і проблема дослідження; вивчалася педагогічна, методична література з даної теми; аналізувалася робота вчителів початкових класів у галузі методики розв’язування задач на рух; формулювалася гіпотеза та завдання дослідження. В процесі експериментального етапу (2007–2008 навчальний рік) – на основі напрацьованої теоретичної інформації здійснювався формуючий експеримент, пов’язаний із формуванням у молодших школярів умінь і навичок розв’язування задач на рух, вивчалася його ефективність та практична значущість.

Експериментальне дослідження ми проводили у НВК «ЗОШ І-ІІІ ступенів №1 – гімназія» м. Копичинці Гусятинського району Тернопільської області. Формуючим експериментом було охоплено 26 учнів 4 класу. У процесі формуючого експерименту ми пропонували четвертокласникам добірку задач на рух різних видів. Ці задачі використовувалися як на уроках, так і на позакласних заняттях з математики для самостійної роботи учнів.

Покажемо методику опрацювання задачі на зустрічний рух, яка проводилася у процесі експериментального дослідження.

У ході підготовчої роботи ми ілюстрували зміст таких виразів, як «виїхали одночасно», «рухаються назустріч один одному». Практичні дії супроводжувалися зображенням відрізків (довжина шляху) і стрілками (напрям руху).

Задача. Два зайчики бігли назустріч один одному. Швидкість одного – 12 м/сек, а другого – 10 м/сек. На скільки метрів зайчики наблизяться один до одного за 5 сек?

–  Чи можна одразу відповісти на запитання задачі? (Ні). Чому?

– Що потрібно знати, щоб відповісти на запитання задачі? (Відстані, які пробігли зайчики).

– Чи можемо ми знайти, яку відстань пробіг перший зайчик за 5 сек? Другий зайчик за 5 сек? (Так.)

– Як ми знайдемо відстані? Потім ми зможемо відповісти на запитання задачі? (Так).

– Яку дію виконаємо? (Додавання).

– Як записати розв'язання задачі у вигляді виразу? (12 • 5 + 10 • 5 = 110 (м)). – Скільки дій ми виконали? (3).

– Чи можна розв'язати задачу іншим способом? (Так).

– На скільки метрів наближаються зайчики один до одного за 1 сек?

– Як ви знайшли? (12 + 10 = 22 м/сек).

– 22 м/сек можна назвати швидкістю зближення. А за 5 сек зайчики наблизяться на більшу відстань, чи не так?

– У скільки разів більшу? (У 5 разів).

– Як записати розв'язання у вигляді виразу? (12+10) • 5 = 22 • 5 = 110 (м).

– Відповідь така сама? Тому можна розв'язувати задачу і таким способом.

–   Скільки дій ви виконали?

–   Який спосіб більш раціональний?

Проілюструємо методику роботи над розв’язуванням задачі на зустрічний рух двома способами.

Задача. З двох міст одночасно назустріч один одному виїхали велосипедист і мотоцикліст, які зустрілися через 3 год. Швидкість велосипедиста 12 км/год, а мотоцикліста – 50 км/год. Скільки кілометрів становить відстань між містами?

Повторюючи задачу, ми опиралися на таку ілюстрацію.

Аналіз проводили від числових даних.

– Що відомо про рух велосипедиста? (Швидкість і час руху).

– Про що звідси можна дізнатися? (Про відстань, яку проїхав велосипедист до зустрічі).

– Що відомо про рух мотоцикліста і що можна знайти? (Відомі швидкість і час, можна знайти відстань).

– Чи можна знайти відстань між містами? (Так).

Далі учні повідомляли план розв'язування задач і записували розв'язання.

Розв'язання

1) 12 • 3 = 36 (км) проїхав велосипедист;

2) 50 • 3 = 150 (км) проїхав мотоцикліст;

3) 36 + 150 = 186 (км) – відстань між містами.

Відповідь. 186 км.

Після повторення розв'язання ми повідомляли, що задачу можна розв'язати іншим способом.

– Спробуємо знайти другий спосіб розв'язування задачі. Велосипедист і мотоцикліст рухалися 3 год. Чи можна знайти, на скільки кілометрів зближувалися велосипедист і мотоцикліст за одну годину? (Можна. Для цього треба додати відстані, які подолали за годину окремо велосипедист і мотоцикліст).

– Велосипедист і мотоцикліст зближувалися 3 год. Як знайти відстань, яку вони подолали за цей час? (Треба помножити суму швидкостей велосипедиста і мотоцикліста на час їх руху).

Розв'язання

1) 12 + 50 = 62 (км) – зближувалися велосипедист і мотоцикліст за годину;

2) 62 • 3 = 186 (км) – відстань між містами.

Відповідь. 186 км.

Підсумовуючи розв'язання задачі другим способом, ми звертали увагу на те, що велосипедист і мотоцикліст проїхали 3 рази по 62 км.

Подальша експериментальна робота зводилася до підбору задач на рух різних видів та їх методично правильного розв’язування. Для формування уявлень про зустрічний рух ми пропонували таку добірку задач.

1. Відстань між двома містами 250 км. З цих міст назустріч один одному одночасно виїхали 2 автобуси. Яка відстань буде між автобусами, коли перший з них проїде 127 км, а другий – 93 км?

Складіть графічну схему умови задачі.

2. З пристані «Київ» до пристані «Кременчук» вирушив теплохід і одночасно йому назустріч з пристані «Кременчук» вирушив катер. Теплохід йшов зі швидкістю 30 км/год, а катер – 24 км/год. Через 5 год вони зустрілися. Яка відстань між пристанями?

Складіть графічну схему умови задачі і розв'яжіть її за діями двома способами.

3. З Харкова до Запоріжжя виїхав мотоцикл і одночасно назустріч йому із Запоріжжя виїхав моторолер. Швидкість мотоцикла 55 км/год, а моторолера – 30 км/год. Через 3 год вони зустрілися. Яка відстань між містами?

Розв'яжіть задачу, склавши числовий вираз.

4. З двох залізничних станцій, відстань між якими 910 км, одночасно вирушили назустріч один одному два електропоїзди і зустрілися через 5 год. Швидкість першого електропоїзда 87 км/год. Яка швидкість другого електропоїзда?

Складіть: графічну схему умови задачі, числовий вираз розв'язання; задачу, обернену до даної, у якій треба дізнатися, через скільки годин відбудеться зустріч.

5. Із села до міста, відстань між якими 48 км, виїхав велосипедист і одночасно назустріч йому з міста виїхав гусеничний трактор. Швидкість велосипедиста 14 км/год, а трактора – 10 км/год. Через скільки годин вони зустрінуться?

Розв'яжіть задачу, склавши числовий вираз.

6. Відстань між містами А і Б 900 км. З міста А в місто В вирушив вантажний автомобіль і одночасно назустріч йому з міста В вирушив легковий автомобіль. Усю відстань вантажний автомобіль пройшов за 15 год, а легковий – за 10 год. Через скільки годин після виїзду автомобілі зустрілися? Розв'яжіть задачу, склавши числовий вираз.

7. Складіть задачі, аналогічні до попередньої; за числовими вираза-ми: 1) (900: 6 – 60) • 6; 2) (900 – 90 • 6): 6.

Складіть схеми до умов цих задач.

8. З пункту А до пункту В вийшов турист зі швидкістю 4 км/год, а через 1 год 30 хв йому назустріч з пункту В вийшов другий турист зі швидкістю 3 км/год. Через 2 год вони зустрілися. Яка відстань між пунктами А і В?

Складіть графічну схему умови задачі та розв'яжіть її за діями і склавши числовий вираз.

9. Відстань між пунктами А і В 30 км. З пунктів А і В одночасно назустріч один одному вийшли два туристи. Через 2 год відстань між ними становила 12 км. Турист, що йшов з пункту В, зупинився і почав чекати першого туриста, який дістався до нього через 3 год. Які швидкості туристів?

Складіть: графічну схему умови задачі; числовий вираз для швидкості другого туриста.

10. Відстань між пунктами А і В 36 км. З пунктів А і В одночасно назустріч один одному вийшли два туристи. Через деякий час відстань між ними становила 18 км, а ще через 2 год вони зустрілися. Відомо, що швидкість одного з туристів більша, ніж швидкість другого, на 1 км/год.

Які запитання можна скласти до задачі? Дайте відповідь на ці запитання.

11. З протилежних берегів ставка одночасно відпливли назустріч один одному два плавці. Перший плив зі швидкістю 40 м/хв, другий – 60 м/хв. Між плавцями весь час курсує моторний човен: від першого до другого і назад і т. д. Швидкість човна – 24 км/год. Яку відстань пройшов човен до моменту зустрічі плавців, якщо відстань між берегами ставка в цьому місці дорівнює 600 м? Задачу розв'яжіть за діями.

1. З пункту А одночасно в протилежних напрямах виїхали колісний і гусеничний трактори. Швидкість колісного трактора 30 км/год, а гусеничного – 10 км/год. На скільки віддаляються трактори один від одного за 1 год? Через скільки годин відстань між тракторами буде 120 км?

Складіть: графічну схему умови задачі; задачу, обернену до даної, щоб невідомою була швидкість одного з тракторів.

2. Складіть задачі, аналогічні до попередньої, за виразами:

1) (120 – 30 • 3): 3; 2) (120: 3 – 10) • 3.

3. З пункту А одночасно у протилежних напрямах виїхали два автомобілі. Через 4 год відстань між ними становила 440 км. Яка швидкість автомобілів, якщо швидкість одного з них на 10 км/год менша за швидкість другого?

4. З пункту А виїхав велосипедист зі швидкістю 14 км/год. Через 2 год з цього ж пункту у протилежному напрямку виїхав вантажний автомобіль зі швидкістю 58 км/год. Через скільки годин після виходу автомобіля відстань між ним і велосипедистом становитиме 244 км?

Складіть графічну схему умови задачі і розв'яжіть її, склавши числовий вираз.

5. Складіть задачу за графічною схемою і виразом: (284 – 12 • 7): 10.

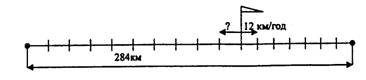
6. З пункту А одночасно у протилежних напрямах виїхали 2 автомобілі. Перший автомобіль їхав зі швидкістю 60 км/год. Через 2 год, коли відстань між ними була 260 км, другий автомобіль зупинився на 1 год, а перший продовжував рух. Через який час від початку руху автомобілів відстань між ними становитиме 710 км?

Знайдіть швидкість другого автомобіля, склавши 2 числових вирази і за допомогою рівняння.

7. З одного аеродрому у протилежних напрямах одночасно вилетіли 2 літаки. Швидкість першого була на 165 км/год більша, ніж швидкість другого. Через деякий час перший з них пролетів 1425 км, а другий – 1920 км. Які швидкості літаків?

Складіть схему синтетичного способу розбору задачі і розв'яжіть за діями.

Для формування уявлень про рух в одному напрямку ми пропонували школярам таку добірку задач:

1. По шосе зі швидкістю 14 км/год їде велосипедист, а вслід йому зі швидкістю 50 км/год їде мотоцикліст. Через який час мотоцикліст наздожене велосипедиста, якщо відстань між ними 108 км? Яку відстань за цей час проїде мотоцикліст? На скільки більше кілометрів за цей час проїде мотоцикліст, ніж велосипедист?

Складіть: графічну схему умови задачі; дві задачі, обернені до даної.

2. Електропоїзд вийшов зі станції зі швидкістю 60 км/год. Через 2 год з тієї ж станції в тому самому напрямку вийшов другий електропоїзд. З якою швидкістю він має йти, щоб наздогнати перший електропоїзд за 6 год?

Складіть: графічну схему умови задачі; задачу, обернену до даної. Розв'яжіть за діями і склавши числовий вираз.

3. Два велосипедисти виїхали одночасно з міста А в місто В, відстань між якими 120 км. Перший велосипедист першу половину шляху їхав зі швидкістю 12 км/год, а другу – 10 км/год. Другий велосипедист увесь час їхав зі швидкістю 11 км/год. Хто з них раніше приїхав до міста В?

Використайте схему.

4. Лисиця помітила зайця, коли той був на відстані 600 м від неї. Зайцю до місця, де він міг би сховатися від лисиці, бігти 2 км 160 м. Чи впіймає лисиця зайця, якщо бігтиме зі швидкістю 870 м/хв? (Швидкість зайця – 720 м/хв).

Відповідь обґрунтуйте. Розв'яжіть задачу двома способами.

5. Петрик почав наздоганяти Олега, коли той був від нього на відстані 960 м, і наздогнав його через 8 хв. Швидкість Олега у 2 рази менша, ніж швидкість Петрика. Яка швидкість Петрика?

Розв'яжіть, склавши числовий вираз і рівнянням. Складіть задачу, обернену до даної.

6. З пункту А в пункт В, відстань між якими 160 км, одночасно виїжджають 2 мотоциклісти. Швидкість першого 40 км/год і він дістається до пункту В на 1 год раніше, ніж другий мотоцикліст. Яка швидкість другого мотоцикліста? Розв'яжіть задачу рівнянням.

7. Відстань між містами А і В 150 км. З міста А до міста В одночасно виїжджають 2 автомобілі. Швидкість першого автомобіля на 10 км/год більша, ніж швидкість другого, і він дістається до міста В за З год. На якій відстані від міста А у цей час знаходиться другий автомобіль?

Розв'яжіть, склавши числовий вираз.

8. Від однієї пристані вирушили в одному напрямку катер і буксир. Швидкість катера 27 км/год, а буксира – 18 км/год. Яка відстань буде між ними через 3 год?

Розв'яжіть задачу двома способами.

9. З села виїхав віз зі швидкістю 7 км/год. Коли він проїхав 20 км, вслід за ним з села виїхав вершник зі швидкістю 12 км/год. Через який час вершник наздожене віз і на якій відстані від села?

Зробіть скорочений запис умови задачі у вигляді таблиці і графічну схему умови. Накресліть схему аналітичного способу розбору задачі і розв'яжіть за діями.

10. Два велосипедисти виїхали одночасно з міста до спортивного табору. Перший їхав зі швидкістю 10 км/год, а другий – 13 км/год. Через 2 год другий велосипедист проколов камеру, тому далі йшов пішки зі швидкістю 4 км/год. На якій відстані від міста перший велосипедист наздожене другого?

Складіть графічну схему умови задачі. Розв'яжіть за діями.

Для формування у молодших школярів уявлень про рух за течією чи проти течії ми пропонували таку добірку задач.

1. Теплохід їде річкою проти течії. За кожну годину він долає 16 км. Яка швидкість течії річки і яка власна швидкість руху теплохода, якщо за течією теплохід рухається зі швидкістю 20 км/год?

Для відповіді на перше запитання використайте рівняння.

2. Відомо, що швидкість теплохода за течією річки на 6 км/год більша, ніж швидкість його проти течії. Яку відстань пройде теплохід за течією за 3 год, якщо його власна швидкість у 6 разів більша, ніж швидкість течії?

Розв'яжіть за діями.

3. За течією моторний човен пройшов а км за 4 год. Цю саму відстань проти течії він пройшов за 6 год. На скільки швидкість човна за течією більша, ніж швидкість його проти течії? (а = 72). Запишіть розв'язання задачі у вигляді виразу з буквою а та обчисліть його.

4. Моторний човен пройшов проти течії річки 16 км за 2 год і повернувся назад за 1 год 20 хв. Яка швидкість течії і яка власна швидкість човна? Скільки часу спускатиметься пліт за течією на відстань 16 км?

Розв'яжіть задачу за діями.

5. Вниз по річці турист проплив 12 км на плоту, а повернувся на човні. Увесь час склав 10 годин. На плоту турист плив на 2 год більше, ніж на човні. Яка швидкість течії і яка власна швидкість човна?

Розв'яжіть задачу за діями.

6. Від пристані А одночасно у протилежних напрямах по річці вирушають пліт, що йде вниз за течією, і моторний човен, що йде проти течії. Швидкість течії 3 км/год, а власна швидкість моторного човна 12 км/год. Яка відстань буде між плотом і човном через 5 годин? На якій відстані від пристані А знаходитимуться окремо човен і пліт через 5 годин? Через скільки годин відстань між плотом і моторним човном становитиме 84 км?

7. Відстань між пристанями А і В – 90 км. Від пристані А вниз за течією у напрямку до пристані В спускається пліт. Одночасно назустріч плоту з пристані В вирушає катер. Швидкість течії 3 км/год, швидкість катера у стоячій воді – 15 км/год. Яка відстань буде між катером і плотом через 2 год? Через який час відбудеться зустріч катера з плотом? На якій відстані від пристані В буде пліт через 2 год? На якій відстані від пристані А буде катер через 2 год?

8. Мандрівник плив на плоту 3 доби. Швидкість течії річки 2 км/год. Далі мандрівник сів у моторний човен і проплив вниз за течією за 6 год відстань, що у 2 рази більша, ніж попередня. Яка власна швидкість човна?

Складіть графічну схему умови задачі і розв'яжіть її за діями.

9. Буксир йде проти течії річки і долає відстань в 285 км між двома портами за 19 год. Скільки часу потрібно буксиру, щоб повернутися назад, якщо швидкість течії 2 км/год?

Складіть: схему аналітичного способу розбору і числовий вираз розв'язання.

Для формування у молодших школярів поняття середньої швид-кості руху ми пропонували їм таку добірку задач.

1. Велосипедист перші 6 год їхав зі швидкістю 14 км/год, а останні 6 год – 10 км/год. Яка середня швидкість руху велосипедиста?

2. Велосипедист першу половину шляху проїхав зі швидкістю 15 км/год, а другу – 10 км/год. Яка середня швидкість руху велосипедиста, якщо довжина шляху складає 300 км?

3. Велосипедист проїхав 60 км. З год він їхав до обіду зі швидкістю 14 км/год і 2 год він їхав після обіду. З якою швидкістю їхав велосипедист після обіду і яка була його середня швидкість на всьому шляху?

4. Два велосипедисти виїхали одночасно з міста А до міста В, відстань між якими 120 км. Перший велосипедист першу половину шляху їхав зі швидкістю 12 км/год, а другу – 10 км/год. Другий велосипедист увесь час їхав зі швидкістю 11 км/год. Хто з них раніше приїхав до міста В? Знайдіть середню швидкість першого велосипедиста.

5. Відстань між двома містами 300 км. Автомобіль пройшов її в одному напрямку зі швидкістю 50 км/год, а у зворотному – 75 км/год. З якою середньою швидкістю рухався автомобіль?

6. Відстань між містом і селом 36 км. З міста в село кінь біг зі швидкістю 12 км/год. Назад він повертався з вантажем зі швидкістю 6 км/год. Яка середня швидкість руху коня?

Виявлення ефективності розробленої системи вправ і задач у формуванні математичних уявлень і понять у молодших школярів ми здійснювали на основі порівняння сформованості відповідних навичок та вмінь в учнів експериментального класу порівняно з контрольним, де використовувалася звичайна система навчання.

На основі відповідних показників ми визначили уміння і навички, пов’язані із розв’язуванням різновидів задач на рух. При цьому виділені уміння ми згрупували у три типи – пропедевтичні, загальні та практичні.

Проаналізуємо дані уміння.

1. Пропедевтичні уміння:

—   уміння демонструвати рухи у різних напрямках і різновидах (назустріч, у протилежному напрямку, у зустрічному напрямку, за течією, проти течії);

—   уміння визначати швидкість свого руху пішки;

—   уміння порівнювати швидкість власного руху і швидкість транспорту;

—   уміння порівнювати швидкість руху різних видів транспорту;

—   уміння будувати креслення на основі умовних позначень.

2. Загальні уміння:

—   уміння визначати зв’язки між величинами «час», «швидкість», «відстань» (сюди входять мікроуміння знаходити швидкість за часом і відстанню, відстань за швидкістю і часом і час за швидкістю і відстанню);

— уміння розв’язувати прості і складені задачі за допомогою арифметичних дій;

— уміння складати і розв’язувати обернені задачі;

— уміння складати план розв’язування задачі;

— уміння розв’язувати задачі двома способами.

3. Практичні уміння:

— уміння розв’язувати задачі на зустрічний рух (сюди входять мікроуміння визначати швидкість зближення і час руху до зустрічі (час зближення), якщо два тіла одночасно (неодночасно) почали рухатися назустріч одне одному з однаковими (неоднаковими) швидкостями);

— уміння розв’язувати задачі на рух у протилежних напрямках (сюди входять мікроуміння визначати швидкість віддалення і час віддалення, якщо два тіла одночасно (неодночасно) почали рухатися з одного пункту у протилежних напрямках з однаковими (неоднаковими) швидкостями);

— уміння розв’язувати задачі на рух в одному напрямку (сюди входять мікроуміння визначати швидкість зближення (віддалення) і час зближення (віддалення);

— уміння розв’язувати задачі на рух в одному напрямку (сюди входять мікроуміння визначати швидкість зближення (віддалення) і час зближення (віддалення);

— уміння розв’язувати задачі на рух за течією чи проти течії (сюди входять мікроуміння визначати власну швидкість катера, швидкість катера за течією, швидкість катера проти течії, швидкість зближення і час зближення, коли катер наздоганяє пліт; швидкість зближення і час зближення, коли катер рухається назустріч плоту, швидкість віддалення і час віддалення, коли катер і пліт рухаються з одного пункту у протилежних напрямках;

— уміння розв’язувати задачі на рух по колу (сюди входять мікроуміння визначати швидкість зближення (віддалення) під час руху в одному напрямку і швидкість зближення (віддалення) під час руху у протилежних напрямках);

— уміння розв’язувати задачі на визначення середньої швидкості руху (сюди входять мікроуміння визначати середню арифметичну величину і середню швидкість як середню арифметичну величину).

За рівнем розвитку даних умінь ми визначили три рівні сформованості математичних уявлень і понять четвертокласників про рух і задачі на рух:

1) високий – у школяра сформовані пропедевтичні уміння, пов’язані із поняттям швидкості, часу та відстані, він може будувати креслення на основі умовних позначень, володіє навичкою розв’язування простих і складених задач, розв’язує обернені задачі, може розв’язувати задачі двома способами на основі самостійно складеного плану розв’язування. Окрім цього, у нього сформовані уміння розв’язувати різновиди задач на рух і здатність безпомилкового виконання завдань або самостійного виправлення допущених помилок при зауваженні вчителя;

2) середній – учень виконує усі попередні завдання на належному рівні, але припускається кількох неістотних помилок, які виправляє з незначною допомогою вчителя;

3) низький – в учня не сформовані пропедевтичні уміння розв’язування задач на рух, не розвинені загальні уміння розв’язування задач і відповідно не сформовані практичні уміння розв’язування власне задач на рух.

Робота, яка проводилася нами в експериментальному класі, позитивно вплинула на підвищення якості знань і вмінь молодших школярів. Так, учні експериментального класу значно краще виконали запропоновані завдання, ніж учні контрольного. Покажемо сформованість умінь і навичок розв’язування задач на рух на рівні відповідних умінь в учнів експериментального і контрольного класів (див. табл. 1–3).

Таблиця 1. Сформованість пропедевтичних умінь в учнів експериментального і контрольного класів

Таблиця 2. Сформованість умінь визначати зв’язки між величинами в учнів експериментального і контрольного класів

Таблиця 3. Сформованість практичних умінь в учнів експериментального і контрольного класів

Отримані результати формуючого експерименту підтвердили гіпотезу, що використання запропонованої системи задач на рух позитивно вплинуло на формування відповідних уявлень і понять в учнів експериментального класу. Таким чином, ми отримали результати, які підтвердили ефективність формуючого експерименту. Із 26 учнів експериментального класу 6 школярів продемонстрували високий рівень розвитку математичних уявлень і понять, 16 – середній і 4 – низький.

У контрольному класі (24 учні) високий рівень розвитку математичних уявлень і понять має 2 учні, середній – 14 і низький 8 школярів. Порівняно з початком експерименту, показники сформованості відповідних умінь зросли в обох класах (початковий рівень відповідно 22 і 24%). Проте в експериментальному класі показники виявилися значно вищими (відповідно 76 і 82% – див. діаграму).

Діаграма. Загальний рівень сформованості математичних уявлень і понять в експериментальному і контрольному класах на початку і в кінці експерименту

Отже, у процесі використання розробленої системи задач на рух в учнів експериментального класу порівняно з контрольним значно підвищився рівень сформованості відповідних знань і умінь, що свідчить про ефективність застосовуваного напрямку роботи. Проведення експериментального дослідження дало змогу виявити і оцінити вищу ефективність використання пропонованої системи задач і простежити процес розвитку уявлень про рух і навичок розв’язування задач на рух порівняно з навчанням дітей в контрольному класі.

Висновки

Отже, значення математики у розвитку школярів як науки і навчального предмета важко перебільшити. Підтвердженням цього є цілий ряд педагогічної та методичної літератури з проблеми дослідження, серед яких чільне місце займають праці В. Московченка. та Л. Дудки.

Розв’язування задач займає значне місце у початковому курсі математики. При цьому термін «задача» вживається в різних значеннях і передбачає необхідність свідомого пошуку відповідних засобів для досягнення мети, яку добре видно, але яка безпосередньо недосяжна. У психологічному аспекті задача розглядається як свідома мета, що існує в певних умовах, а дії – як процеси, спрямовані на розв'язування задачі.

У навчанні математики задачі становлять специфічний розділ програми, матеріали якого учні мають засвоїти, і виступають як дидактичний засіб навчання, виховання і розвитку школярів. У методиці математики розрізняють математичні та арифметичні задачі. Під математичною задачею розуміють будь-яку вимогу обчислити, побудувати, довести що-небудь, що стосується кількісних відношень і просторових форм, побудованих людським розумом. Арифметичною задачею називають вимогу знайти числове значення деякої величини, якщо дано числові значення інших величин і лінійну залежність, яка пов'язує ці величини як між собою, так і з шуканою. У системі навчання учнів початкових класів загальноосвітньої школи переважають арифметичні задачі. Задачі на побудову, найпростіші доведення, а також завдання логічного порядку займають порівняно незначне місце.

Важливе значення для розв'язування текстових задач у навчальному процесі має ретельний добір навчальних завдань, які мають відповідати певним загально-методичним вимогам: забезпечувати засвоєння учнями програмового матеріалу з математики і, зокрема, формувати в них знання про задачу, її склад і процес розв'язування, вчити використовувати набуті знання в різних ситуаціях. При цьому зміст завдань має відповідати темі уроку і меті вивчення матеріалу, а числові дані – програмовим вимогам; послідовність застосування вправ має сприяти свідомому засвоєнню теоретичних знань і вмінню розв'язувати задачі, розвитку прийомів розумової і творчої діяльності школярів; забезпечувати автоматизацію елементарних дій, з яких складається діяльність при розв'язуванні задач; створювати умови для узагальнення способів діяльності; відповідати логіці й структурі процесу формування вмінь. Кількість задач повинна відповідати психологічним особливостям школярів і бути достатньою для формування певного вміння або навички.

Розв'язування задачі – це процес перетворення її умови, який здійснюється на основі знань з тієї галузі, до якої належить задача, певних логічних правил виводу і особливих правил інтуїтивного (евристичного) характеру. В найбільш загальному плані цей процес складається з таких етапів: аналіз задачі, пошук плану розв'язування; здійснення знайденого плану розв'язування; з'ясування того, що здобутий результат задовольняє вимогу задачі; аналіз розв'язування.

Дидактичні особливості задач на рух пов’язані з принципами навчання, формами організації навчальної роботи та методами навчання. Методика математики враховує дані дидактики, але в їх використанні відображає особливості своєї науки. У кожному з етапів задач на рух відчутні загальні положення дидактики.

Підготовча робота до розв'язування задач на рух передбачає узагальнення уявлень дітей про рух; ознайомлення з новою величиною – швидкістю, розкриття зв'язків між величинами: швидкість, час, відстань. Для узагальнення уявлень дітей про рух корисно проводять спеціальну екскурсію для спостереження за рухом транспорту, після чого організовують спостереження за рухом в умовах класу.

Під час роботи над задачами на рух можна виділити такі основні поняття: зустрічний рух (швидкість зближення; час зближення); рух у протилежних напрямках (швидкість віддалення; час віддалення); рух в одному напрямі (швидкість зближення (віддалення); час зближення (віддалення)); рух за течією чи проти течії (власна швидкість плавзасобу; його швидкість за течією; проти течії; швидкість зближення і час зближення; швидкість віддалення і час віддалення); рух по колу (швидкість зближення (віддалення) під час руху в одному і протилежних напрямках); середня швидкість руху (середня арифметична величина; середня швидкість).

Чималі труднощі під час розв'язування задач на рух у середніх та старших класах визначаються недостатньою роботою над даним типом задач у початковій школі. Однією з причин цього є недостатня сформованість у початкових класах понять про величини (час, відстань, швидкість) та їх пропорційну залежність. У молодших школярів необхідні поняття можливо формувати як на матеріалі чинних підручників початкових класів, так і доповнюючи його задачами, складеними на підґрунті типових задач, призначених для учнів середніх класів.

Проведення експериментального дослідження дало змогу оцінити ефективність використання пропонованої системи задач і простежити процес розвитку уявлень про рух і навичок розв’язування задач даного типу. У процесі використання розробленої нами системи задач на рух в учнів експериментального класу порівняно з контрольним значно підвищився рівень сформованості відповідних знань і умінь, що свідчить про ефективність застосовуваного напрямку роботи та його доцільність у навчанні математики молодших школярів.

Список літератури

1. Бантова М.О. Методика викладання математики в початкових класах. – К.: Вища школа, 1982. – 288 с.

2. Басангова Р.Е. Стимулювання пізнавальної діяльності учнів в ході розв’язування задач // Поч. школа. – 1989. – №1. – С. 40–44.

3. Белова Е.С. Развитие диалога в процессе решения школьниками мыслительных задач // Вопр. психологии. – 1991. – №2. – С. 148–153.

4. Богданович М.Б. Дидактичний матеріал з математики для 3-го класу. – К.: Рад. школа, 1977. – 34 с.

5. Богданович М.Б. Методика розв’язування задач у початковій школі. – К.: Вища школа, 1990. – 183 с.

6. Богданович М.Б., Козак М.В., Король Я.А. Методика викладання математики в початкових класах: Навч. пос. – Тернопіль: Навч. книга – Богдан, 2001. – 368 с.

7. Богданович М.В. Математика: Підручник для 4 кл. чотириріч. поч. шк. – К.: Освіта, 1994. – 226 с.

8. Богданович М.В. Урок математики в початковій школі: Пос. для вчителя. – К.: Рад. школа, 1990. – 192 с.

9. Василенко І.З. Методика викладання математики в початкових класах. – К.: Просвіта, 1971. – 376 с.

10. Возрастные возможности усвоения знаний / Под. ред. Д.Б. Эльконина, В.В. Давыдова. – М.: Педагогика, 1966. – 232 с.

11. Вопросы дидактики и психологии начального обучения / Под. ред. Б.Г. Ананьева. – Л.: Лен. НИИ пед. АПН РСФСР, 1959. – 98 с.

12. Газдун М.І. Як учити молодших школярів розв’язувати задачі // Поч. школа. – 1988. – №11. – С. 70–72.

13. Глушков И.К. Дифференцированная работа над задачами // Нач. школа. – 1985. – №2. – С. 34–35.

14. Гнеденко Б.В. Развитие мышления и речи при изучении математики // Матем. в школе. – 1991. – 31. – С. 3–9.

15. Гора Т., Логачевська С. Диференційований підхід до розв'язування текстових задач // Поч. школа. – 2002. – №1. – С. 17–22.

16. Друзь Б.Г. Творчі вправи з математики для початкових класів. – К.: Рад. школа, 1988. – 144 с.

17. Заїка А., Богданович М. Учням про задачу і процес її розв’язування // Початкова школа. – 2000. – №11. – С. 28–29.

18. Занков Л.В. Беседы с учителем: Вопросы обучения в начальных классах. – М.: Педагогика, 1970. – 142 с.

19. Захарова А.М. Розвивальне навчання математики в початковій школі // Психол. і педагогіка. – 2000. – №1. – С. 21–27.

20. Истомина Н.Б., Шикова В.Н. Формирование умений решать задачи различными способами // Нач. школа. – 1985. – №9. – С. 50–54.

21. Король Я.А. Математика в початкових класах: Культура усного і писемного мовлення. – Тернопіль: Навч. книга – Богдан, 2000. – 160 с.

22. Король Я.А. Піднесення культури математичної мови // Поч. школа. – 1995. – №1. – С. 11–12.

23. Король Я.А. Практикум з методики викладання математики в початкових класах. – Тернопіль: Мандрівець, 1998. – 136 с.

24. Король Я.А. Розв’язування текстових задач різними способами // Актуальні проблеми розбудови національної освіти. Ч. ІІІ. – К.-Херсон, 1997. – С. 76–78.

25. Король Я.А. Формування практичних умінь і навичок на уроках математики. – Тернопіль: Навч. книга – Богдан, 2000. – 136 с.

26. Король Я.А., Чайка Н.М. Вдосконалення методики роботи над задачами геометричного змісту // Поч. школа. – 1995. – №10–11. – С. 19–22.

27. Корчевська О.П., Козак М.В. Робота над задачами в 4 класі. Поурочні розробки. – Тернопіль: Астон, 2002. – 204 с.

28. Кочина Л., Листопад Н. Математика: навчальні програми для чотирирічної початкової школи // Поч. школа. – 2001. – №7. – С. 17–20.

29. Кочина Л.П., Листопад Н.П. Математика, 4 клас – К.: Літера ЛТД, 2004. – 176 с.

30. Крутецкий В.А. Психология математических способностей школьников. – М.: Просвещение, 1968. – 204 с.

31. Кухар В.М., Паюл В.М. Скорочений запис задач // Початкова школа. – 1978. – №4. – С. 44–48.

32. Литовченко З.М. Карапузова Н.Д. Культура усного мовлення на уроках математики // Поч. школа. – 1984. – №2. – С. 31–34.

33. Маркова А.А. Формирование мотивации обучения в школьном возрасте. – М.: Педагогика, 1983. – 124 с.

34. Матюша І.К. Гуманізація виховання і навчання в загальноосвітній школі. – К.: Просвіта, 1995. – 122 с.

35. Менчинская Н.А., Моро М.И. Вопросы методики и психологии обучения арифметике в начальных классах. – М.: Просвещение, 1965. – 268 с.

36. Методы начального обучения математике. Сб.статей / Под ред. Л.Н. Скаткина. – М.: Просвещение, 1975. – 284 с.

37. Методика начального обучения математике / Под общ. ред. А.А. Столяра, В.Л. Дрозда. – Мн.: Асвета, 1988. – 268 с.

38. Методика начального обучения математике / Под ред. Л.Н. Скаткина. – М.: Просвещение, 1972. – 340 с.

39. Моро М.И. Карточки с арифметическими задачами для 3-го класса. – М.: Просвещение, 1972. – 36 с.

40. Моро М.И., Пишкало А.М. Методика навчання математики в 1–3 класах. – К.: Рад. школа, 1979. – 376 с.

41. Московченко В., Дудко Л. Розв’язування математичних задач на рух // Початкова школа. – 2000. – №11. – С. 25–27.

42. Московченко В., Дудко Л. Розв’язування математичних задач на рух // Початкова школа. – 2000. – №12. – С. 14–15.