Межпредметные связи в школьном обучении

Межпредметные связи в школьном обучении

Содержание

Введение

Глава 1. Межпредметные связи.

§ 1. Понятие и классификация межпредметных связей.

1.1 Виды межпредметных связей в содержании обучения математики.

§ 2. Функции межпредметных связей.

§ 3. Планирование межпредметных связей.

§ 4. Способы реализации и планирование межпредметных связей в обучении математики и биологии.

Глава 2. Примеры реализации межпредметных связей.

Лабораторная работа №1 "Растворы, смеси и сплавы".

Лабораторная работа №2 "Площадь. Квадрат числа".

Лабораторная работа №3 "Окружность и круг".

Лабораторная работа №4 "Сумма углов треугольника".

Лабораторная работа №5 "Процент".

Лабораторная работа №5' "Прцент".

Лабораторная работа №6 "Составление рациона".

Заключение

Список использованной литературы

Введение

В настоящее время, пожалуй, нет необходимости доказывать важность межпредметных связей в процессе преподавания. Они способствую лучшему формированию отдельных понятий внутри отдельных предметов, групп и систем, так называемых межпредметных понятий, то есть таких, полное представление о которых невозможно дать учащимся на уроках какой-либо одной дисциплины (понятия о строении материи, различных процессах, видах энергии).

Современный этап развития науки характеризуется взаимопроникновением наук друг в друга, и особенно проникновением математики и физики в другие отрасли знания.

Связь между учебными предметами является прежде всего отражением объективно существующей связи между отдельными науками и связи наук с техникой, с практической деятельностью людей.

Необходимость связи между учебными предметами диктуется также дидактическими принципами обучения, воспитательными задачами школы, связью обучения с жизнью, подготовкой учащихся к практической деятельности.

Межпредметные связи в школьном обучении являются конкретным выражением интеграционных процессов, происходящих сегодня в науке и в жизни общества. Эти связи играют важную роль в повышении практической и научно-теоретической подготовки учащихся, существенной особенностью которой является овладение школьниками обобщенным характером познавательной деятельности.

Осуществление межпредметных связей помогает формированию у учащихся цельного представления о явлениях природы и взаимосвязи между ними и поэтому делает знания практически более значимыми и применимыми, это помогает учащимся те знания и умения, которые они приобрели при изучении одних предметов, использовать при изучении других предметов, дает возможность применять их в конкретных ситуациях, при рассмотрении частных вопросов, как в учебной, так и во внеурочной деятельности, в будущей производственной, научной и общественной жизни выпускников средней школы. С помощью многосторонних межпредметных связей не только на качественно новом уровне решаются задачи обучения, развития и воспитания учащихся, но также закладывается фундамент для профессионального самоопределения учащихся средних общеобразовательных школ. Именно поэтому межпредметные связи являются важным условием и результатом комплексного подхода в обучении и воспитании школьников. Межпредметные связи следует рассматривать как отражение в учебном процессе межнаучных связей, составляющих одну из характерных черт современного научного познания.

При всем многообразии видов межнаучного взаимодействия можно выделить три наиболее общие направления:

1. Комплексное изучение разными науками одного и тоже объекта.

2. Использование методов одной науки для изучения разных объектов в других науках.

3. Привлечение различными науками одних и тех же теорий и законов для изучения разных объектов.

В современных условиях возникает необходимость формирования у школьников не частных, а обобщенных умений, обладающих свойством широкого переноса. Такие умения, будучи сформированными в процессе изучения какого-либо предмета, затем свободно используются учащимися при изучении других предметов и в практической деятельности.

В настоящее время в связи с увеличением объема информации, подлежащего усвоению в период школьного обучения, и в связи с необходимостью подготовки всех учащихся к работе по самообразованию особо важное значение приобретает изучение роли межпредметных связей в активизации познавательной деятельности учащихся.

Глава 1. Межпредметные связи

§ 1. Понятие и классификация межпредметных связей

В педагогической литературе имеется более 30 определений категории "межпредметные связи", существуют самые различные подходы к их педагогической оценке и различные классификации.

Так, большая группа авторов определяет межпредметные связи как дидактическое условие, причем у разных авторов это условие трактуется неодинаково.

Например: межпредметные связи выполняют роль дидактического условия повышения эффективности учебного процесса (Ф.П. Соколова); межпредметные связи как дидактическое условие, обеспечивающее последовательное отражение в содержании школьных естественнонаучных дисциплин объективных взаимосвязей, действующих в природе (В.Н. Федорова, Д.М. Кирюшкин). Ряд авторов дает такие определения межпредметных связей:

"Межпредметные связи есть отражение в курсе, построенном с учетом его логической структуры, признаков, понятий, раскрываемых на уроках других дисциплин", или такое: Межпредметные связи представляют собой отражение в содержании учебных дисциплин тех диалектических взаимосвязей, которые объективно действуют в природе и познаются современными науками [1].

Все выше перечисленные определения конечно верно, однако их нельзя считать полными. Для того чтобы вывести наиболее правильное и информативное определение понятию «межпредметные связи», надо подвести его под другое, более широкое. Таким более широким, родовым понятием по отношению к категории «межпредметная связь» является понятие «межнаучная связь», но и первое и второе являются производными от общего родового понятия «связь» как философской категории. Отсюда становится очевидным, что «межпредметные связи» есть, прежде всего, педагогическая категория, и сущностной основой ее является связующая, объединяющая функция. Исходя из этого, можно сделать определение: межпредметные связи есть педагогическая категория для обозначения синтезирующих, интегративных отношений между объектами, явлениями и процессами реальной действительности, нашедших свое отражение в содержании, формах и методах учебно-воспитательного процесса и выполняющих образовательную, развивающую и воспитывающую функции в их ограниченном единстве.

Разнообразие высказываний о педагогической функции межпредметных связей объясняется многогранностью их проявления в реальном учебном процессе. Кроме того, сказывается недостаточный учет связи педагогики с другими науками. [2].

Рассмотрим теперь классификацию межпредметных связей, так как правильная классификация, отображая закономерности развития классифицируемых понятий, глубоко вскрывает связи между ними, способствует созданию научно-практических предпосылок для реализации этих связей в учебном процессе.

Межпредметные связи характеризуются, прежде всего, своей структурой, а поскольку внутренняя структура предмета является формой, то мы можем выделить следующие формы связей:

по составу.

по направлению действия.

по способу взаимодействия направляющих элементов.

Исходя из того, что состав межпредметных связей определяется содержанием учебного материала, формируемыми навыками, умениями и мыслительными операциями, то в первой их форме мы можем выделить следующие типы межпредметных связей:

содержательные;

операционные;

методические;

организационные.

Каждый тип первой формы подразделяется на виды межпредметных связей. (См. Таб.1).

Во второй форме выделяем основные типы межпредметных связей по направлению действия. Обозначим соотносящиеся стороны связи условно буквами A, B, C, D и т.д.

В случае если В направлено к А , то будем иметь одностороннюю связь,

если В и С направлены к А , то эта связь будет двусторонней;

если же B, C, D… и т.д. будут направлены к А, то эта связь будет многосторонней .

Все эти типы связей могут быть прямыми (действовать в одном направлении) и обратными, или восстановительными, когда они будут действовать в двух направлениях: прямом и обратном.

Например  -- прямая односторонняя связь;  - двусторонняя обратная, или восстановительная связь.

В третьей форме межпредметных связей, по временному фактору, выделяют следующие типы связей:

хронологические;

хронометрические.

Хронологические -- это связи по последовательности их осуществления.

Хронометрические – это связи по продолжительности взаимодействия связеобразующих элементов.

Каждый из этих двух типов подразделяется на виды межпредметных связей. (См. Табл.1).

Таблица 1.

Классификация межпредметных связей.

Межпредметные связи по составу показывают -- что используется, трансформируется из других учебных дисциплин при изучении конкретной темы.

Межпредметные связи по направлению показывают:

является ли источником межпредметной информации для конкретно рассматриваемой учебной темы, изучаемой на широкой межпредметной основе, один, два или несколько учебных предметов.

Используется межпредметная информация только при изучении учебной темы базового учебного предмета (прямые связи), или же данная тема является также «поставщиком» информации для других тем, других дисциплин учебного плана школы (обратные или восстановительные связи).

Временной фактор показывает:

какие знания, привлекаемые из других школьных дисциплин, уже получены учащимися, а какой материал еще только предстоит изучать в будущем (хронологические связи);

какая тема в процессе осуществления межпредметных связей является ведущей по срокам изучения, а какая ведомой (хронологические синхронные связи).

как долго происходит взаимодействие тем в процессе осуществления межпредметных связей.

Вышеприведенная классификация межпредметных связей позволяет аналогичным образом классифицировать внутрикурсовые связи (связи, например, между ботаникой, зоологией, анатомией и общей биологией – курса биологии; связи между неорганической и органической химией – курса химии…), а также внутрипредметные связи между темами определенного учебного предмета, например ботаники, органической химии, новейшей истории. Во внутрикурсовых и внутрипредметных связях из хронологических видов преобладают преемственные и перспективные виды связей, тогда как синхронные резко ограничены, а во внутрипредметных связях синхронный вид вообще отсутствует.

1.1 Виды межпредметных связей в содержании обучения математики

Совокупность функций межпредметных связей реализуется в процессе обучения тогда, когда учитель математики осуществляет все многообразие их видов. Различают связи внутрицикловые (связи математики с физикой, химией) и межцикловые (связи математики с историей, трудовым обучением). Виды межпредметных связей делятся на группы, исходя из основных компонентов процесса обучения (содержания, методов, форм организации): содержательно-информационные и организационно-методические.

Содержательно- информационные межпредметные связи делятся по составу научных знаний, отраженных в программах математических курсов, на фактические, понятийные, теоретические, философские.

Межпредметные связи на уровне фактов (фактические) - это установление сходства фактов, использование общих фактов, изучаемых в курсах физики, химии, математики, и их всестороннее рассмотрение с целью обобщения знаний об отдельных явлениях, процессах и объектах изучения. Так, в обучении математики и химии учителя могут использовать математику для вычисления химического состава вещества.

Понятийные межпредметные связи - это расширение и углубление признаков предметных понятий, и формирование понятий, общих для родственных предметов (общепредметных). К общепредметным понятиям в курсах естественнонаучного цикла относятся понятия теории строения веществ - пропорции, следствия, движение, масса и т.п. Эти понятия широко используются при изучении процессов. При этом они углубляются, конкретизируются на математическом материале и приобретают обобщенный, общенаучный характер.

Теоретические межпредметные связи - это развитие основных положений общенаучных теорий и законов, изучаемых на уроках по родственным предметам, с целью усвоения учащимися целостной теории.

§ 2. Функции межпредметных связей [3]

Межпредметные связи в школьном обучении являются конкретным выражением интеграционных процессов, происходящих сегодня в науке и в жизни общества. Эти связи играют важную роль в повышении практической и научно-теоретической подготовки учащихся. С помощью многосторонних межпредметных связей закладывается фундамент для комплексного видения, подхода и решения сложных проблем реальной действительности.

Межпредметные связи выполняют в обучении математике ряд функций.

Методологическая функция выражена в том, что только на их основе возможно формирование у учащихся диалектико-материалистических взглядов на природу, современных представлений о ее целостности и развитии, поскольку межпредметные связи способствуют отражению в обучении методологии современного естествознания, которое развивается по линии интеграции идей и методов с позиций системного подхода к познанию природы.

Образовательная функция межпредметных связей состоит в том, что с их помощью учитель математики формирует такие качества знаний учащихся, как системность, глубина, осознанность, гибкость. Межпредметные связи выступают как средство развития математических понятий, способствуют усвоению связей между ними и общими естественнонаучными понятиями.

Развивающая функция межпредметных связей определяется их ролью в развитии системного и творческого мышления учащихся, в формировании их познавательной активности, самостоятельности и интереса к познанию природы. Межпредметные связи помогают преодолеть предметную инертность мышления и расширяют кругозор учащихся.

Воспитывающая функция межпредметных связей выражена в их содействии всем направлениям воспитания школьников в обучении математике. Учитель математики, опираясь на связи с другими предметами, реализует комплексный подход к воспитанию.

Конструктивная функция межпредметных связей состоит в том, что с их помощью учитель биологии совершенствует содержание учебного материала, методы и формы организации обучения. Реализация межпредметных связей требует совместного планирования учителями предметов естественнонаучного цикла комплексных форм учебной и внеклассной работы, которые предполагают знания ими учебников и программ смежных предметов.

Забота о построении содержания единого курса математики, усиление его внутренних связей не принижают значения его взаимосвязи с другими учебными предметами. Межпредметные связи в обучении рассматриваются как дидактический принцип и как условие, захватывая цели и задачи, содержание, методы, средства и формы обучения различным учебным предметам.

Межпредметные связи позволяют вычленить главные элементы содержания образования, предусмотреть развитие системообразующих идей, понятий, общенаучных приемов учебной деятельности, возможности комплексного применения знаний из различных предметов в трудовой деятельности учащихся. Межпредметные связи влияют на состав и структуру учебных предметов. Каждый учебный предмет является источником тех или иных видов межпредметных связей. Поэтому возможно выделить те связи, которые учитываются в содержании математики, и, наоборот, идущие от математики в другие учебные предметы.

Формирование общей системы знаний учащихся о реальном мире, отражающих взаимосвязи различных форм движения материи - одна из основных образовательных функций межпредметных связей. Формирование цельного научного мировоззрения требует обязательного учета межпредметных связей.

Таким образом, межпредметность -- это современный принцип обучения, который влияет на отбор и структуру учебного материала целого ряда предметов, усиливая системность знаний учащихся, активизирует методы обучения, ориентирует на применение комплексных форм организации обучения, обеспечивая единство учебно-воспитательного процесса [4].

§ 3. Планирование межпредметных связей

Содержание, объем, время и способы использования знаний из других предметов можно определить только на основе планирования. Для этого необходимо тщательное изучение рекомендаций, данных учебными программами в разделах «Межпредметные связи» по каждой учебной теме курса, а также изучение учебных планов и материала учебников смежных предметов.

В практике обучения сложились четыре основных способа планирования межпредметных связей -- сетевое, курсовое, тематическое и поурочное.

Сетевое планирование.

Оно осуществляется завучем или председателем методической или предметной комиссии по определенному циклу, группе предметов. Сетевое планирование имеет форму графика или плана-карты, которые выявляют основные связи разных учебных тем смежных курсов, показывают узловые темы с наибольшим числом связей с другими предметами.

Сетевой график представляет собой модель учебного процесса, которая отражает содержание и объем учебной деятельности учащихся в определенные отрезки времени и с учетом межпредметных связей.

На рисунке указаны последовательность тем различных курсов и наличие связей в их содержании. Двойным кружком обозначены узловые темы, имеющие наибольшее число связей с другими предметами (математика, физика, химия).

Такая модель наглядно показывает логику построения смежных учебных предметов, их взаимосвязи, наиболее важные, узловые темы, временные связи в изучении зависящих друг от друга вопросов и т.п. Модель в виде сетевого графика является важным средством управления учебным процессом. На ее основе руководители школы могут внести коррективы в расписание, проконтролировать своевременность прохождения особо важных учебных тем.

Посещение уроков по узловым темам, связывающим знания учащихся по нескольким предметам, дает возможность руководителю школы увидеть предшествующую работу других учителей, усвоение учащимися нужных понятий, заранее спланировать и сократить общее количество посещений уроков.

Дополнением к сетевому графику служит планкарта, в которой отражается не только последовательность изучения учебных тем, но и комплекс развиваемых понятий в смежных предметах.

Сетевое планирование дает общую канву межпредметных связей в цикле учебных предметов, но недостаточно организует активную познавательную деятельность учащихся. Необходимо планирование методов и форм организации обучения при осуществлении межпредметных связей. Этому способствуют другие способы планирования.

Курсовое планирование.

Планирование межпредметных связей внутри учебного курса может осуществляться учителем или методистом. При этом могут существовать разные подходы к анализу межпредметных связей. Наиболее распространён тематический подход, т.е. на последовательный анализ межпредметных связей от одной учебной темы к другой.

Межпредметные связи рекомендуется использовать в сочетании с внутри предметными связями. Наличие курсового плана позволяет учителю заранее изучить необходимое для каждой последующей учебной темы содержание смежных курсов, вовремя дать учащимся домашние задания на повторение опорных знаний из других предметов. При использовании курсового плана возможно заранее спланировать консультации и посещения уроков учителей других предметов, подобрать необходимую методическую литературу по межпредметным связям в каждой учебной теме.

Так же используется проблемный подход к курсовому планированию межпредметных связей. При этом выделялась общая для всего курса учебная проблема мировоззренческого характера. Она позволяла систематизировать знания из разных предметов под углом зрения определенной идеи, которая объединяла все учебные темы курса.

Разновидностью проблемного подхода является планирование в курсе межпредметных связей с целью развития ведущих научных понятий. В качестве примера приведем планирование в курсе математики в целях развития ведущих математических понятий. При таком планировании учитель ориентируется на установление главным образом понятийных межпредметных связей. Это важно для развития математического мышления. Но такая работа должна иметь вспомогательный характер. Нельзя упускать из виду все многообразие межпредметных связей в процессе обучения, которые лишь в совокупности обеспечивают формирование целостной системы взглядов на мир и мировоззрения школьников. Поэтому важно сочетать и разные подходы к планированию межпредметных связей при изучении учебного курса.

На основе курсового планирования необходимо провести тематическое планирование межпредметных связей, особенно в узловых учебных целях.

Тематическое планирование.

В тематическом плане должна быть отражена логическая структура учебного материала уроков, опорные знания из других курсов и перспективные связи. Составляя тематический план, учитель наглядно видит, для чего, с какой познавательной целью на отдельных уроках необходимо использовать те или иные задания из других курсов:

в одних случаях создается опора для введения новых понятий,

в других объясняются причинно-следственные связи в изучаемых явлениях,

в третьих конкретизируются общие идеи или доказываются выводы, новые теоретические положения и т.п.

В зависимости от познавательных целей использования межпредметных связей отбираются методы и приемы их осуществления, формулируются вопросы и задания для учащихся.

Общая схема тематического планирования межпредметных связей может быть представлена в форме таблицы:

Тема «...................»      Класс «................»

Данная форма может быть изменена учителем в зависимости от конкретных условий установления межпредметных связей в обучении. Такое планирование создаёт у учителя общее представление о том, какие знания и из каких предметов необходимо учащимся повторить к каждому уроку, какие понятия и знания из других предметов следует привлечь к раскрытию основных понятий учебной темы и какие мировоззренческие идеи будут развиваться на основе межпредметных связей. Знания из разных предметов помогают поднять обобщение учебного материала темы на мировоззренческий уровень.

Такое планирование учитывает многообразие видов межпредметных связей и позволяет выделить основные направления активизации познавательной деятельности учащихся в процессе изучения учебной темы. В целях эффективной организации учебно-познавательной деятельности учеников по осуществлению межпредметных связей полезно спланировать их систему на каждом уроке учебной темы.

Поурочное планирование.

Конкретизация использования межпредметных связей в процессе обучения достигается с помощью поурочного планирования. Поурочный план-разработка показывает, когда, на каком этапе урока и как, какими способами включаются знания из других курсов в изучение нового или закрепление учебного материала. Особенно необходима тщательная разработка обобщающего урока с межпредметными связями. Выделение таких уроков производится на основе тематического планирования.

Положительные стороны данной разработки -- это формулировка цели и задач урока с учетом межпредметных связей; формулировка конкретных вопросов к учащимся, требующих воспроизведения и применения знаний по физике; определение понятий; наличие мировоззренческого вывода, обобщающего факты и законы математики и физики; включение в домашнее задание вопросов межпредметного содержания.

Составляя поурочные планы, учителю важно знать, что учащиеся уже освоили из необходимых опорных знаний на уроках по другим предметам, согласовать с учителями смежных предметов постановку вопросов и заданий, чтобы избежать дублирования и достигнуть развития общих идей и понятий, их углубление и обогащения. Этому помогает посещение уроков и изучение составляемых коллегами планов реализации межпредметных связей.

Планы могут быть обсуждены на методических комиссиях по циклам предметов, согласованы с завучем школы. Обсуждение планов позволяет предупредить ошибки в использовании знаний из других предметов, устранить неточности в формулировке вопросов, в трактовке понятий смежных курсов, определить единые подходы в объяснении сущности изучаемых процессов и явлений, избрать наиболее рациональные методы обучения.

Таким образом, планирование составляет необходимое и существенное звено подготовки учителя к эффективному осуществлению межпредметных связей и является одним из средств их реализации в практике обучения школьников.

§ 4. Способы реализации и планирование межпредметных связей в обучении математики и биологии

Использование межпредметных связей - одна из наиболее сложных методических задач учителя математики. Она требует знаний содержания программ и учебников по другим предметам. Реализация межпредметных связей в практике обучения предполагает сотрудничество учителя с учителями химии, физики, посещения открытых уроков, совместного планирования уроков и т.д.

Учитель математики с учетом общешкольного плана учебно-методической работы разрабатывает индивидуальный план реализации межпредметных связей в математических курсах. Методика творческой работы учителя включает ряд этапов:

1) изучение раздела "Межпредметные связи" по каждому математическому курсу и опорных тем из программ и учебников других предметов, чтение дополнительной научной, научно-популярной и методической литературы;

2) поурочное планирование межпредметных связей с использованием курсовых и тематических планов;

3) разработка средств и методических приемов реализации межпредметных связей на конкретных уроках;

4) разработка методики подготовки и проведения комплексных форм организации обучения;

5) разработка приемов контроля и оценки результатов осуществления межпредметных связей в обучении.

Рассмотрим межпредметные связи математики и биологии.

Хотя в биологии широко используются результаты и методы, заимствованные из чистой математики, сама она по существу представляет собой прикладную научную дисциплину.

В биологии специалисты не могут выполнять важные исследования, не прибегая к непосредственному сотрудничеству с учеными математиками, которые в процессе своей подготовки не получают глубоких биологических знаний. Поэтому сотрудничество между этими специалистами является важной особенностью почти всех научных исследований в области биологии.

Существуют ситуации, когда требуется весьма незначительное сотрудничество. Так, биолог, имеющий некоторую математическую подготовку, сможет довольно точно вывести дифференциальное уравнение в частных производных, описывающее сложный физиологический процесс, однако он не сможет найти его решение. Эту задачу можно передать непосредственно математику с простой просьбой “получить ответ”. Такой порядок может оказаться удовлетворительным, если не возникнут какие-либо затруднения. В этом случае работа математика носит преимущественно вспомогательный характер, и настоящего сотрудничества здесь не требуется.

Однако вполне возможно, что для решения уравнений нужны некоторые дополнительные условия или допущения, либо их трудно решить именно в той форме, в какой они представлены. В этом случае математик может ввести дополнительные ограничения или произвести некоторые изменения, позволяющие решить эти уравнения. Но может оказаться, что произведенные им изменения не соответствуют духу первоначальной биологической задачи, и в результате будет затрачено много сил на сложные, но бесполезные математические расчеты в поисках точного решения ошибочной задачи.

Для того чтобы математик узнал, что именно, в конечном счете, допустимо с точки зрения биологии, он должен проявить интерес к самой биологической задаче и познакомиться с ней во всех деталях. Тесное сотрудничество между математиком и биологом должно начинаться по возможности на самом начальном этапе научно-исследовательской работы и продолжаться до ее завершения. Биолог должен быть готов скорректировать или изменить свои концепции и гипотезы в соответствии с возможностями математических и вычислительных методов, а математику не придется двигаться в ложном направлении.

В значительной мере этому способствует развитие взаимосвязи между биологией и математикой ещё в средней общеобразовательной школе, требующей проведения консультаций и научных исследований на стыке между математическим и биологическим предметами. Часто такое сотрудничество оказывается очень полезным и в других важных областях, возникших на стыке нескольких различных дисциплин.

Глава 2. Примеры реализации межпредметных связей

В современном мире множество отраслей, связанных с химией, например такие, как пищевая, фармацевтическая, тяжёлая промышленность (производство сплавов чёрных и цветных металлов), медицина, фармакология и т.д. Однако все они связаны не только с химией, но и с математикой, так как приходится решать задачи на процентное содержание в продукте питания, металле, лекарстве, косметике и т.д. тех или иных веществ.

Задачи на смеси и сплавы при первом знакомстве с ними вызывают у учащихся общеобразовательных классов затруднения. Самостоятельно справиться с ними могут немногие.

Трудности при решении этих задач могут возникать на различных этапах:

составления математической модели (уравнения, системы уравнений, неравенства и т. п.;

решения полученной модели;

анализа математической модели (по причине кажущейся ее неполноты: не хватает уравнения в системе и пр.).

Однако при тщательном анализе задачи, вышеуказанные трудности преодолимы. Этому способствуют чертежи, схемы, таблицы и пр. Каждый учащийся сам для себя делает вывод об уровне сложности той или иной задачи и месте, где эта сложность возникает.

Основными компонентами в этих задачах являются:

масса раствора (смеси, сплава);

масса вещества;

доля (% содержание) вещества.

При решении большинства задач этого вида, удобнее использовать таблицу, которая нагляднее и короче обычной записи с пояснениями. Зрительное восприятие определенного расположения величин в таблице дает дополнительную информацию, облегчающую процесс решения задачи и её проверки.

Лабораторная работа в 9 классе №1 (интегрированный урок математика + химия)

Тема: «Растворы, смеси и сплавы»

Цели:

Обучающая:

Обобщение, углубление, систематизация знаний, умений, навыков учащихся, развитие творческих способностей учащихся;

Развитие практических умений (пользовать приборами класса химии, составление уравнений и пропорций);

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической терминологией;

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся.

Оборудование: пробирки с водой, раствором уксусной кислоты (70%), мензурка с делениями.

Повторить дома понятия и формулы:

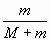-- доля вещества в растворе;

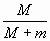-- доля воды в растворе;

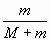· 100 % -- концентрация раствора, или процентное содержание вещества в растворе;

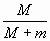· 100% -- процентное содержание воды в растворе;

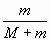· 100 % + 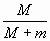· 100% = 100%.

Примечание 1. Лабораторная проводится в классе химии;

Примечание 2. Вместо весовых мер вещества и воды можно брать доли или части.

Цель работы:

Знакомство с практическим применением знаний, полученных на уроках математики при изучении другого предмета (химии);

Решение задач на растворы, смеси и сплавы с помощью таблицы;

Изготовление раствора с заданным процентным содержанием вещества;

ХОД РАБОТЫ

Ознакомьтесь с условием задачи.

Выделите основные компоненты задачи, занесите их в таблицу.

Таблица для решения задач имеет следующий вид:

Решите задачу, при необходимости, обратитесь за помощью к учителю математики.

С помощью учителя химии приготовьте раствор, используя полученные из решения задачи данные.

Задача 1.Сколько нужно добавить воды в сосуд, содержащий 200 г 70 % -го раствора уксусной кислоты, чтобы получить 8 % раствор уксусной кислоты?

Решение.

Анализируя таблицу, составляем уравнение :

0,08(200 + х) = 0,7·200

16 + 0,08х = 140

0,08х = 124

х = 1550

Ответ : 1,55 кг воды.

Ответьте на вопросы и выполните задание:

В какой профессии может использоваться данная задача?

Встречались ли вы ранее с такой задачей, если да, то где?

Решите дома к следующему уроку химии задачу:

Задача 2. В сосуд, содержащий 2 кг 80 % -го водного раствора уксуса добавили 3 кг воды. Найдите концентрацию получившегося раствора уксусной кислоты.

Решение.

Масса уксусной кислоты не изменилась, тогда получаем уравнение:

0,01х·5 = 0,8·2

0,05х = 1,6

х = 1,6:0,05

х = 32

Ответ: 32 %.

Дополнительные вопросы и задания:

Составить и решить задачу на проценты.

Решить задачу:

Задача 3: Для получения 20,3г сульфата бария взяли 12,1 г серной кислоты. Сколько сульфата бария получится, если взять 36,3 г серной кислоты? (один ученик решает задачу на доске с комментированием)

Решение:

1.Запишем уравнение химической реакции:

BaCl +HSO= Ba SO+2 HCl

2.Запишем известные и неизвестные числовые значения над формулой веществ в уравнении:

36,3 г x г

BaCl +HSO= Ba SO+2 HCl

12,1 г 20,3 г

3. Составим и решим пропорции:

г – масса сульфата бария

Ответ: m(Ba SO)=60,9 г

Лабораторная работа в 6 классе №2 (интегрированный урок математика + охрана природы)

Тема: «Площадь. Квадрат числа»

Цели:

Обучающая:

Обобщение, углубление, систематизация знаний, умений, навыков учащихся, развитие творческих способностей учащихся (поиск решения нестандартной задачи);

Развитие практических умений (измерение длин, перевод из одних единиц измерения в другие);

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической и экологической терминологией;

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся.

Оборудование: линейка, учебник «Математика 5», Латотин Л.А., Чеботаревский Б.Д..

Повторить дома понятия и формулы:

a, b—стороны прямоугольника;

 – площадь прямоугольника;

1 м² = 100 дм² = 10000 см²;

1 га = 100 а = 10000 м²

Примечание 1. Найти в Интернете на сайте #"Рисунок 81" src="/wimg/9/465230.files/image015.gif" alt="#">га леса);

Цель работы:

Знакомство с практическим применением математики в жизни на примере профессии эколога;

Решение задачи на вычисление количества га леса для изготовления тиража учебника;

Развитие качества бережливости по отношению к учебникам;

ХОД РАБОТЫ

Задача.

Вычислить, сколько нужно вырубить леса для того, чтобы издать один учебник “Математика 6” авт. Л. А. Латотин, Б.Д. Чеботаревский и сколько, чтобы издать тираж учебника?

1. Вычислить площадь одной страницы учебника (измерить на уроке).

2. Умножить результат на количество страниц в учебнике (посмотреть количество страниц в конце учебника)

3. Умножить на тираж учебника (посмотреть тираж)

4. Выразить результат в квадратных метрах.

5. Сколько вырубили леса, чтобы создать тираж учебника?

Решение.

Размеры одной страницы учебника 14см на 21 см, т.е. площадь равна

В учебнике 318 страниц или 159 листа, значит площадь всех листов учебника . На 1000 м² нужно вырубить 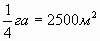деревьев, т.е. в 2,5 раза больше. Значит на производство одного учебника требуется . На весь тираж в 42200 экземпляров требуется:

леса, а это примерно 5 га

Ответ: 5 га

Дополнительные вопросы и задания:

Какие леса преобладают на территории Беларуси?

Запишите в тетради определения равных фигур и их свойства.

В современном мире, в связи с тем, что человек всё больше использует богатства природы, необходима такая профессия как эколог. Экологи следят за состоянием окружающей среды, помогают избежать истребления лесов, популяций животных, загрязнения рек, озёр, морей и океанов. Контролируют количество вредных выбросов производства. Эту профессию выбирают люди, которым не безразлична судьба природы, которые заботятся о ней.

На рассмотренном примере мы убедились в том, что экологи так же должны знать математику, для своей эффективной работы.

Теперь, зная сколько леса уничтожается для изготовления учебников, подумайте, прежде чем их портить!!!

Лабораторная работа в 5 классе №3 (сам)

Тема: «Окружность и круг»

Цели:

Обучающая:

Получить теоретическое и практическое представление об окружности и круге, как геометрических фигурах, их элементов;

Развитие практических умений – пользоваться чертёжными инструментами, с их помощью строить окружности любого радиуса;

Повторить способ сравнения отрезков одинаковой и разной длины.

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической терминологией (путём распознания);

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся.

Оборудование: простой карандаш, линейка, циркуль, ластик, учебник (Математика 5, Л.А. Латотин, Б.Д. Чеботаревский), окружности и круги разных диаметров.

Повторить:

Измерение и сравнение отрезков.

Цель работы:

Знакомство с геометрическими фигурами – окружность и круг;

Изучение их элементов;

Построение окружности и круга;

Измерение радиусов окружности и круга.

ХОД РАБОТЫ

Поставьте на листе точку. Обозначьте её буквой О.

Проделайте с циркулем следующее: ножку циркуля с иглой установите в точку О, а ножку с грифелем вращайте вокруг данной точки, касаясь листа тетради. Итогом будет замкнутая линия, которую и называют окружностью. Точку О называют центром окружности.

Начертите отрезки, концами которых будут точка О и точка на замкнутой линии. Эту точку обозначьте большой буквой.

Ответьте на вопросы и выполните задание:

Сколько таких отрезков можно провести?

Сравните эти отрезки.

Сделайте вывод.

Запишите вывод в тетрадь.

(Такой отрезок называется радиусом окружности). Запишите определение в тетрадь.

Найдите в учебнике определение радиуса окружности.

Ответьте на вопросы и выполните задание:

Что можно сказать о расположении точек окружности по отношению к центру окружности?

Запишите определение в тетради: отрезок, проходящий через центр окружности и имеющий своими концами две точки окружности, называется диаметром.

Сколько диаметров можно провести в окружности на вашем рисунке?

Измерьте длину диаметра на своем рисунке.

Сравните длину диаметра с длиной радиуса.

Сделайте вывод.

Запишите вывод в тетрадь.

Что делает диаметр с окружностью?

Найдите в учебнике определение части окружности. Запишите в тетрадь.

На сколько дуг делит диаметр окружность?

Соедините две точки окружности ( этот отрезок называется хордой). Запиши в тетрадь.

Ответьте на вопросы:

Сколько хорд можно провести в окружности? Ответ запишите в тетради.

Может ли хорда проходить через центр? Ответ поясните. Если “Да”, то как ее можно назвать по-другому?

Запишите определение диаметра через понятие хорды.

Изучите круг и его свойства.

Окружность поделила плоскость тетради на две части. Та часть, которая лежит внутри окружности вместе с окружностью, называется кругом.

Изобразите круг в своей тетради.

Измерьте длину его радиуса.

Сравните его с диаметром.

Запишите свои наблюдения.

Запишите все, что ты можешь сказать о круге.

Сравните свои наблюдения с окружностью и сделайте выводы о фигуре, которая называется кругом.

Дополнительные вопросы и задания:

Измерьте радиусы окружностей и кругов, имеющихся у вас.

Запишите, чему равны диаметры каждой из фигур.

Запишите, какие выводы ты сделал?

Нарисуйте окружность произвольного радиуса. Изобразите все изученные вами элементы окружности и подпишите их.

Нарисуйте две окружности, которые не пересекаются. Измерьте длины их радиусов, расстояние между их центрами и сделайте вывод. Запишите в тетрадь.

Нарисуйте две окружности, которые пересекаются в двух точках. Измерьте длины их радиусов, расстояние между их центрами и сделайте вывод. Запишите в тетрадь.

Нарисуйте две окружности, которые имеют одну общую точку. Измерьте длины их радиусов, расстояние между их центрами и сделайте вывод. Запишите в тетрадь.

Приведите примеры окружности и круга в окружающих вас предметах.

Лабораторная работа в 5 классе №4 (сам)

Тема: «Сумма углов треугольника»

Цели:

Обучающая:

Получить теоретическое и практическое представление о формуле суммы углов треугольника;

Развитие практических умений – пользоваться чертёжными инструментами, с их помощью строить углы, треугольники с разными углами;

Повторить понятия “смежные и вертикальные углы”, “прямой, острый, тупой угол”, “способы измерения углов”.

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической терминологией (путём распознания);

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся;

Воспитание усидчивости и внимательности.

Оборудование: простой карандаш, линейка, транспортир, ластик, учебник (Математика 5, Л.А. Латотин, Б.Д. Чеботаревский), треугольники с разными углами при вершинах.

Повторить:

Определение угла;

Измерение и сравнение углов.

Цель работы:

Знакомство с формулой суммы углов треугольника;

Измерение градусной меры углов.

Построение углов и треугольников;

ХОД РАБОТЫ

На листе бумаги проведите произвольно луч АВ – одну из сторон угла.

Проделайте с транспортиром следующее: наложите его так, чтобы центр его совпал с началом луча АВ, а сам луч прошёл через нулевое деление шкалы.

На шкале отыщите чёрточку, которая обозначает 45⁰ и около неё поставьте точку С.

При помощи линейки и простого карандаша проведите луч АС – вторую сторону угла.

Соедините точки С и В отрезком. В итоге у вас получился треугольник АВС.

При помощи транспортира измерьте углы С и В. Результаты измерения занесите в тетрадь.

Ответьте на вопросы и выполните задание:

Что можно сказать о сумме углов полученного треугольника? Вывод запишите в тетради.

Запишите свойство углов треугольника в тетради: Сумма углов треугольника равна 180⁰. Формулой это записывается следующим образом А + В + С=180⁰.

Чем можно объяснить, что не у всех полученные числа точно совпадают с числом 180?

Ответьте на вопросы:

Может ли сумма углов треугольника быть больше (меньше) 180⁰?

Запишите алгоритм построения угла заданной меры в тетрадь.

Сравнение углов:

Определите на глаз, какие из изображённых ниже углов являются прямыми, тупыми, острыми. Определения тупого, острого и прямого углов запишите в тетрадь.

Назовите на изображённом ниже рисунке смежные и вертикальные углы. Определения смежного и вертикального угла запишите в тетради.

Дополнительные вопросы и задания:

Постройте у себя в тетради треугольник с углами 45⁰, 90⁰ и 45⁰.

Измерьте длины сторон треугольника, сделайте вывод.

Найдите фотографию Пизанской башни и на ней измерьте примерный угол наклона её по отношению к земле.

Давайте с вами вспомним, в каких профессиях необходимы знания, которые мы научились применять на сегодняшнем уроке.

Я вам помогу и расскажу о такой профессии, как архитектор. Эта профессия появилась несколько тысячелетий назад, когда ещё египтяне строили свои пирамиды. Ведь в этих самых пирамидах углы основания рассчитаны до градуса, иначе они не простояли бы столько времени. Современные небоскрёбы проектируются на компьютерах и углы рассчитываются уже не до градуса, а до секунды.

Ещё одна профессия, в которой необходимо знания по пройденной нами теме – это агроном, ведь ему приходится вычислять размеры участков, форма которых не всегда прямоугольная.

Строители дорог выверяют наклон дорожного покрытия по отношению к горизонту. Если бы они этого не делали мы бы ездили не по ровным дорогам, а по «американским горкам».

А про другие профессии вы мне расскажите на следующем уроке.

Лабораторная работа в 6 классе № 5 (сам) (интегрированный урок математика + медицина)

Тема: «Процент»

Цели:

Обучающая:

Обобщение, углубление, систематизация знаний, умений, навыков учащихся, развитие творческих способностей учащихся;

Развитие практических умений;

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической и медицинской терминологией;

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся.

Оборудование: рулетка, стул, линейка.

Повторить дома правила:

Перевода процентов в десятичную дробь;

Нахождение процента от числа;

Перевода десятичной дроби в проценты;

Нахождения числа по проценту.

Примечание 1. Для проведения работы желательно взять специальную линейку для измерения роста из медкабинета;

Цель работы:

Знакомство с практическим применением математики в жизни на примере профессии врача-хирурга;

Оценка своего физического развития;

Развитие заинтересованности в изучении математики как прикладной науки;

ХОД РАБОТЫ

Задача . Определение пропорциональности своего телосложения.

Измерьте свой рост или рост своего друга стоя;

Измерьте свой рост или рост своего друга сидя;

Воспользовавшись формулой:

где А — показатель пропорциональности телосложения, оцените пропорциональность физического развития по следующей таблице:

Результаты занесите в тетрадь.

Вопросы и задания:

Запишите в тетради определение процента.

Запишите в тетради правило нахождения процента от числа.

Запишите в тетради правило перевода десятичной дроби в проценты и наоборот.

Дополнительные вопросы и задания:

Что вы можете рассказать о профессии хирурга?

В словаре найдите слово «хирург» и запишите в тетради его значение.

Давайте с вами побольше узнаем о людях, которые следят за нашим развитием и корректируют нашу осанку. Этим занимаются люди по профессии своей педиатры (если вам <18 лет), а так же хирурги (если вам > 18 лет). Да именно хирурги, они не только проводят различные операции, но и исправляют осанку, помогают при негармоническом физическом развитии. И педиатры и хирурги помогают людям быть не только здоровыми, но и красивыми. В нашей стране таких людей готовят в медицинских университетах, где обучаются 7 лет.

Лабораторная работа в 6 классе № 5’ (интегрерированный урок математика + медицина)

Тема: «Процент»

Цели:

Обучающая:

Обобщение, углубление, систематизация знаний, умений, навыков учащихся, развитие творческих способностей учащихся;

Развитие практических умений;

Развивающая:

Развитие математической речи, наблюдательности, самостоятельности в учебной деятельности;

Работа над математической и медицинской терминологией;

Развитие непроизвольной памяти.

Воспитательная:

Привитие умения коллективной работы, расширение кругозора;

Развитие познавательной активности учащихся.

Оборудование: рулетка, стул, линейка.

Повторить дома правила:

Перевода процентов в десятичную дробь;

Нахождение процента от числа;

Перевода десятичной дроби в проценты;

Нахождения числа по проценту.

Примечание 1. Для проведения работы желательно взять специальную линейку для измерения роста из медкабинета;

Цель работы:

Знакомство с практическим применением математики в жизни на примере профессии врача-хирурга;

Оценка своего физического развития;

Развитие заинтересованности в изучении математики как прикладной науки;

ХОД РАБОТЫ

Задача. Определение правильность осанки.

измерьте расстояние между крайними костными точками, выступающими над правым и левым плечевым суставами спереди (характеризует ширину плеч);

измерьте расстояние между крайними костными точками, выступающими над правым и левым плечевым суставами сзади (характеризует величину дуги спины);

Воспользовавшись формулой:

%

где А — показатель состояния осанки, оцените состояние осанки по следующей таблице:

Результаты занесите в тетрадь.

Вопросы и задания:

Запишите в тетради определение процента.

Запишите в тетради правило нахождения процента от числа.

Запишите в тетради правило перевода десятичной дроби в проценты и наоборот.

Дополнительные вопросы и задания:

Что вы можете рассказать о профессии хирурга?

В словаре найдите слово «хирург» и запишите в тетради его значение.

Давайте с вами побольше узнаем о людях, которые следят за нашим развитием и корректируют нашу осанку. Этим занимаются люди по профессии своей педиатры (если вам <18 лет), а так же хирурги (если вам > 18 лет). Да именно хирурги, они не только проводят различные операции, но и исправляют осанку, помогают при негармоническом физическом развитии. И педиатры и хирурги помогают людям быть не только здоровыми, но и красивыми. В нашей стране таких людей готовят в медицинских университетах, где обучаются 7 лет.

Лабораторная работа в 11 классе № 6

Данную лабораторную работу дети проводят самостоятельно (из-за нехватки времени на уроке). Результаты приносят учителю математики и он проверяет расчёты, проведённые учащимися.

Задача. Оценка и составление рациона питания включает два направления работы.

1. Определение общего количества калорий, необходимых на день (работа с таблицей). Примерные энергозатраты при разных видах работы (данные приведены в ккал/час на 60 кг массы тела).

Для расчета суточных энергетических затрат перемножьте время (в часах) той или иной деятельности на количество энергии, которая при этом тратится. Нормальным считается, если калорийность пищевого рациона человека превышает энергозатраты не более, чем на 5%.

2. Составление пищевого рациона. Рассчитывают пищевой рацион в зависимости от энергозатрат. Для этого наблюдают свой энергообмен в течение нескольких дней и определяют средние данные. Составляют суточный рацион питания из того расчета, что количество белков, жиров, углеводов, необходимых в сутки, должно примерно отвечать соотношению 1:1:4, и что в сутки подросткам 15-16 лет необходимо примерно 10-120 г белков, 90-110 г жиров, 450-500 г углеводов. Надо помнить, что в рационе должно быть достаточное количество витаминов, микроэлементов.

Используя табличные данные о калорийности различных продуктов, учащиеся составляют меню четырехразового питания так, чтобы на завтрак, обед, полдник и ужин приходилось соответственно 25%, 50, 15, 10% суточного рациона. Результаты расчетов заносят в таблицу.

В жизни данной проблемой занимаются диетологи, они помогают в составлении рациона, подбирают оптимальную диету (кстати, диету должен составлять профессионал, иначе можно навредить своему здоровью). Эта профессия стала актуальной и востребованной в настоящее время, так как наметилась устойчивая тенденция: люди всё больше обращают внимание на своё здоровье, свой внешний облик.

Заключение

Реализация идеи межпредметных связей в педагогике и методике преподавания тесно связано с методологическими воззрениями педагогов на проблему синтеза и анализа научного знания как конкретного выражения дифференциации наук. Теоретическое и практическое решение этой проблемы изменялось в соответствии с развитием общества, его социальным заказам педагогической науки и школе. Утверждение и упрочнение предметной системы преподавания в современной школе неразрывно связано с развитием идеи межпредметных связей.

Выявление и последующее осуществление необходимых и важных для раскрытия ведущих положений учебных тем межпредметных связей позволяет:

снизить вероятность субъективного подхода в определении в определении межпредметной емкости учебных тем.

сосредоточить внимание учителей и учащихся на узловых аспектах учебных предметов, которые играют важную роль в раскрытии ведущих идей наук.

осуществлять поэтапную организацию работы по установлению межпредметных связей, постоянно усложняя познавательные задачи, расширяя поле действия творческой инициативы и познавательной самодеятельности школьников, применяя все многообразие дидактических средств для эффективного осуществления многосторонних межпредметных связей.

формировать познавательные интересы учащихся средствами самых различных учебных предметов в их органическом единстве.

осуществлять творческое сотрудничество между учителями и учащимися.

изучать важнейшие мировоззренческие проблемы и вопросы современности средствами различных предметов и наук в связи с жизнью.

Дальнейшее улучшение системы многосторонних межпредметных связей предполагает и дальнейшее совершенствование путей их реализации:

планирование этой работы в школе,

координацию деятельности всех участников педагогического процесса;

эффективное использование межпредметных (комплексных) семинаров, экскурсий, конференций, расширение практики сдвоенных уроков, на которых могут решаться узловые мировоззренческие проблемы средствами различных учебных предметов и наук одновременно, с участием двух или нескольких учителей.

Список использованных источников

1. Смирнова М.А. Теоретические основы межпредметных связей - М.,2006.

2. Межпредметные связи в учебном процессе. / Под. ред. Дмитриев С.Д. -Киров - Йошкар-Ола: Кировский гос. пед. ин-т, 1978- с.80.

3. BestReferat_ru - Банк рефератов, дипломы, курсовые работы, сочинения, доклады.mht

4. Лошкарева Н.А. Межпредметные связи как средство совершенствования учебно-воспитательного процесса - Вып.5. - М.: МГПИ им.В.И.Ленина, 1981.; Лошкарева Н.А. О понятии и видах межпредметных связей // педагогика. - М., 1972. - №6 - С.48-56.

5. Черкес-Заде Н.М. Межпредметные связи как условие совершенствования учебного процесса: Дис.канд.пед.наук. — М.,1968.