Алгоритмічні проблеми
1.
Алгоритмічні проблеми
Навчаючи
арифметиці в початковій школі, ми познайомилися з додаванням і множенням двох
чисел. Нам у явній формі не говорили, що в будь-якої пари чисел існують добуток
і сума, а вказали способи і правила їхнього знаходження. Такі способи і правила
є прикладами алгоритмів, і обчислювальних (ефективних) процедур.
Їхнє застосування не вимагає чи винахідливості чи кмітливості, учню необхідно
було тільки слідувати інструкціям учителя.
Більш
загально, алгоритм, чи ефективна процедура, – це механічне
правило чи автоматичний метод, чи програма для виконання деяких математичних
операцій. Приведемо ще кілька прикладів операцій, для яких легко можна вказати
алгоритми:
(1.1)
(а) по даному п знайти n-e просте число;
(b)
диференціювання полінома;
(c)
знаходження найбільшого загального дільника двох натуральних чисел (алгоритм
Евклида);
(d)
для двох даних чисел х, у вирішити, чи є х кратним у.
Неформально
і схематично алгоритм представлений на мал. 1а. На вхід подається інформація чи
об'єкт, що підлягає обробці (наприклад, поліном у прикладі (1.1) (b), пари
натуральних чисел у прикладах (1.1) (с) і (d)), а виходом є результат обробки
операції над входом (так, для (1.1) (b) це похідна полінома, а для (1.1) (d) –
відповідь «так» чи «ні»). Вихід виробляється автоматично чорним ящиком-який
може бути комп'ютером або школярем, що діє по інструкції, чи навіть дуже
розумним добре тренованим собакою. Алгоритм є процедура (чи спосіб обчислення),
здійснювана чорним ящиком для одержання виходу з входу.
Якщо
алгоритм, чи ефективна процедура, використовується для обчислення значень
числової функції, то ця функція називається ефективно вычислимой, чи алгоритмічно
вычислимой, чи просто вычислимой. Наприклад, функції ху,
Вхід
вихід
НОД
(х, у)= найбільший загальний дільник чисел х и у и f(n)=
просте число вираховувані в неформальному змісті, як уже відзначалося вище.
Розглянемо,
з іншого боку, наступну функцію:
1,
якщо в десятковому розкладанні числа pi знайдеться
g(n)==
рівно п підряд йдущих цифр 7;
0 у
противному випадку.
алгоритм
предикативний операторний знання
Більшість
математиків вважають, що g є цілком «законною» функцією. Але чи
вираховувана функція g? Існує механічна процедура для послідовного породження
цифр у десятковому розкладанні pi, тому напрошується «процедура» для обчислення
функції g. «При заданому п почніть обчислювати десятковий розклад
pi по одній цифрі за один такт часу і відзначайте появу сімок. Якщо на
якому-небудь кроці з'явиться відрізок, що складається рівно з п сімок,
зупините процес обчислення і покладете g(n)=0. Якщо такий відрізок не
буде обнаружен, то покладете g(n)=0».
Недоліком
цієї «процедури» є та обставина, що якщо для деякого п не існує відрізка
з п – сімок, тоді ні на якому кроці процесу ми не можемо зупинитись і
зробити висновок про те, що цей факт має місце. На кожному даному кроці ми
можемо очікувати, що така послідовність сімок може зустрітися в ще
недослідженній нескінченній частині розкладання pi. Таким чином, ця «процедура»
буде продовжуватися нескінченно довго для усякого входу п, такого, що
g(n)=0; тому вона не є ефективною процедурою. (Можливо, що існує ефективна
процедура для обчислення g, заснована, імовірно, на деяких теоретичних
властивостях числа pi. В даний час, однак, така процедура невідома.)
Цей приклад виявляє дві характерні риси поняття ефективної
процедури, а саме що така процедура відбувається за деяку послідовність кроків
(кожен крок виконується за кінцевий час) і що кожен вихід з'являється після
кінцевого числа кроків.
Дотепер
ми неформально описували поняття алгоритму (чи ефективної процедури) і
зв'язаного з ним поняття обчислюваної функції. Ці поняття мають потребу в
уточненні, перш ніж вони стануть основою для математичної теорії
обчислюваності.
Визначення будуть
дані в термінах простого «ідеалізованого комп'ютера», що виконує програми. Ясно,
що процедури, що можуть бути пророблені реальним комп'ютером, є прикладами
ефективних процедур. Однак кожен окремий реальний комп'ютер обмежений як
величиною чисел, що надходять на вхід, так і розміром доступного робочого
простору (для запам'ятовування проміжних результатів); саме в цьому відношенні
наш «комп'ютер» буде ідеалізованим відповідно до неформальної ідеї алгоритму.
Програми нашої обчислювальної машини будуть кінцевими, і ми скажимо, щоб
обчислення, що завершуються, виконувалися за кінцеве число кроків. Входи і
виходи ми обмежимо натуральними числами; це не є істотним обмеженням, оскільки
операції, що включають інші види об'єктів, можуть бути закодовані як операції
над натуральними числами. (Більш докладно ми зупинимося на цьому в § 5.)
2.
Необхідні поняття, факти і нотація із інших математичних дисциплін
Тут дано огляд
математичних понять і роз'яснимо позначення і терміни, що будуть використані
надалі.
1.
Множини
Для
позначення множин звичайно будуть використовуватися прописні букви А, В, С….
Тут х А позначає, що х є елементом
множини А чи належить множині А, а х
А позначає, що х є елементом
множини А чи належить множині А, а х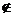 А
означає, що х не належить множині А. Позначення {х/… х…},
де…х… є деяке твердження, що включає х, означає множину всіх
об'єктів х, для яких…х… вірно. Так, {х/х є парним натуральним
числом} є множина {0,2, 4,6,…}.
А
означає, що х не належить множині А. Позначення {х/… х…},
де…х… є деяке твердження, що включає х, означає множину всіх
об'єктів х, для яких…х… вірно. Так, {х/х є парним натуральним
числом} є множина {0,2, 4,6,…}.
Якщо
А, В суть множини, то запис A  В означає, що
А міститься (як частина) в В (чи А є підмножиною В); запис
А
В означає, що
А міститься (як частина) в В (чи А є підмножиною В); запис
А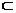 В означає, що А
В означає, що А В, але А
В, але А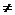 В
(тобто А є власною підмножиною В). Об'єднання множин А, В, є
множина {х| х
В
(тобто А є власною підмножиною В). Об'єднання множин А, В, є
множина {х| х А чи х
А чи х В (чи відразу двом множинам А, В)}
і позначається А U В; перетин А, В є множина {х/х
В (чи відразу двом множинам А, В)}
і позначається А U В; перетин А, В є множина {х/х А і х
А і х В}
і позначається через А
В}
і позначається через А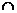 В. Різниця (чи
відносне доповнення) множин А, В є множина {х / х
В. Різниця (чи
відносне доповнення) множин А, В є множина {х / х А
і х
А
і х В} і позначається А\В.
В} і позначається А\В.
Порожня множина позначається через 0. Стандартний символ N
позначає множину натуральних чисел {0, 1, 2, 3,…}. Якщо А – множина натуральних
чисел (тобто А N), то А позначає доповнення
до А до N, тобто N\А. Через N+ позначається множина додатніх
натуральних чисел {1,2,3,…}, а множина цілих чисел позначається через Z.
N), то А позначає доповнення
до А до N, тобто N\А. Через N+ позначається множина додатніх
натуральних чисел {1,2,3,…}, а множина цілих чисел позначається через Z.
Упорядкована пара елементів х, у позначається (х,
у); таким чином, (х, у)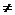 (у, х).
Картезіанським, чи декартовым, добутком множин А и В
називається множина {(х, у)/х
(у, х).
Картезіанським, чи декартовым, добутком множин А и В
називається множина {(х, у)/х А, у
А, у В}, і позначається вона через А
В}, і позначається вона через А В.
В.
Більш
узагальнено, запис (х1…, хn) позначає упорядкований n-набір
(п-ку) елементів х1,…, хn; часто цей n-набір
позначається однією жирною буквою х. Якщо А1,…,
Аn суть множини, те А1 …
… Аn позначає множину n-ок {(х1,…,
хn) /х1
Аn позначає множину n-ок {(х1,…,
хn) /х1  А1 і
х2
А1 і
х2  А2…хn
А2…хn Аn}. Добуток А
Аn}. Добуток А А
А …
… А (п разів) скорочено позначають як Аn;
а А1 означає просто А.
А (п разів) скорочено позначають як Аn;
а А1 означає просто А.
2.
Функції
Ми
припускаємо, що читач знайом з основним поняттям функції і розходженням між
функцією f і окремим значенням f(х) на даному х, на якому
функція визначена. Областю (визначення) функції f називається
множина {x/f(x) визначена} і позначається Dom(f); ми
будемо говорити, що f (х) не визначена, якщо x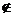 Dom(f).
Множина {f (х) | х
Dom(f).
Множина {f (х) | х  Dom (f)}
називається множиною значень, чи образом (range), функції f
і позначається через Ran (f). Якщо А и В – множиниі,
то будемо говорити, що f є функція з A в В, якщо Dom (f)
Dom (f)}
називається множиною значень, чи образом (range), функції f
і позначається через Ran (f). Якщо А и В – множиниі,
то будемо говорити, що f є функція з A в В, якщо Dom (f) A и Ran(f)
A и Ran(f) В. Коли Dom(f)=A, буде
застосовуватися позначення f: A
В. Коли Dom(f)=A, буде
застосовуватися позначення f: A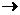 r.
r.
Функція
називається ін’єктивною, якщо з х, у Dom
(f) і х
Dom
(f) і х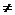 у випливає f(х)
у випливає f(х) 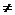 f (у). Для ін’єктивної функції f
через f -1 позначається функція, зворотня до f,
тобто така єдина функція g, що Dom (g)=Ran (f) g (f(x))=x
для всіх х
f (у). Для ін’єктивної функції f
через f -1 позначається функція, зворотня до f,
тобто така єдина функція g, що Dom (g)=Ran (f) g (f(x))=x
для всіх х Dom (f). Функція f з А
в В називається сюр’єктивною, якщо Ran(f)=B.
Dom (f). Функція f з А
в В називається сюр’єктивною, якщо Ran(f)=B.
Якщо f:
A 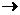 В и функція f ин’єктивна
(сюр’єктивна), то f називається ін'єкцією (з А в В)
(сюр’єкцією (з А в В)). Функція, що є одночасно ін'єкцією і
сюръекцией, називається биекцией.
В и функція f ин’єктивна
(сюр’єктивна), то f називається ін'єкцією (з А в В)
(сюр’єкцією (з А в В)). Функція, що є одночасно ін'єкцією і
сюръекцией, називається биекцией.
Припустимо,
що f є функцією, а Х – множина. Обмеженням f на Х
називається функція з областю визначення Х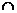 Dom(f),
значення якої в кожному х
Dom(f),
значення якої в кожному х  Х
Х 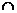 Dom (f) дорівнює f(x).
Dom (f) дорівнює f(x).
Обмеження
f на Х позначається через f|X. Ran (f|X) позначається
через f(X). Якщо Y – множина, то прообразом Y відносно f
називається множина f-1(Y)={x|f(x) Y}.
(Помітимо, що прообраз визначений навіть тоді, коли функція не ин’єктивна.)
Y}.
(Помітимо, що прообраз визначений навіть тоді, коли функція не ин’єктивна.)
Якщо f,
g-функції, то будемо говорити, що g продовжує f, коли Dom (f)
 Dom (g) і f(х) = g (х)
для всіх х
Dom (g) і f(х) = g (х)
для всіх х  Dom (f); у коротшому
запису: f=g/Dom(f). Це відношення функцій f, g записується
як f
Dom (f); у коротшому
запису: f=g/Dom(f). Це відношення функцій f, g записується
як f  g.
g.
Композиція двох функцій f
і g є функція з областю визначення {x/x Dom(g)
і g(x)
Dom(g)
і g(x) Dom(f)}, значення якої, коли вона
визначена, є f (g(x)). Цю функцію позначають через f
Dom(f)}, значення якої, коли вона
визначена, є f (g(x)). Цю функцію позначають через f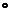 g.
g.
Через
f0 позначаємо ніде не визначену функцію; тобто Dom(f0)=Ran(f0)=0.
Очевидно, що f0=g|0 для будь-якої функції g.
В
обчисленнях нам часто будуть зустрічатися функції чи вирази, що включають
функції, що не усюди визначені. У таких випадках дуже зручне наступне
позначення. Нехай a(x) і b(х) – вирази, що включають змінні х=(х1,…,
хn). Тоді запис а(x)  b(x) означає, що для
кожного х вираження а(x) і b(x) або одночасно визначені і рівні, або
обидва не визначені. Так, наприклад, для функцій f і g запис f(x)
b(x) означає, що для
кожного х вираження а(x) і b(x) або одночасно визначені і рівні, або
обидва не визначені. Так, наприклад, для функцій f і g запис f(x) g(x) означає, що f=g; і для
довільного числа y запис f(x)
g(x) означає, що f=g; і для
довільного числа y запис f(x)  y
означає, що f(x) визначена і дорівнює y (оскільки y завжди
визначене).
y
означає, що f(x) визначена і дорівнює y (оскільки y завжди
визначене).
Функції
від натуральних чисел. У більшій частині цієї книги ми будемо мати
справу з функціями від натуральних чисел, тобто з функціями з Nn в N
для різних п, здебільшого для п = 1 чи 2.
Функція
f з Nn в N називається п-місною функцією. Значення f
на п-кі (x1,…, хn)  Dom (f)
записується як f(x1,…, xn) чи f(x), якщо x
представляє (x1,…, xn). У багатьох книгах і
статтях термін часткова функція використовується для позначення функції
з Nn у N, область визначення якої не обов'язково збігається з Nn.
Для нас слово функція означає часткову функцію. Проте при нагоді ми
будемо писати «часткова функция», щоб підкреслити її можливу «не усюди
визначеність». Тотальною функцією з Nn у N ми називаємо
функцію з Nn у N), область визначення якої є всі Nn. l
Dom (f)
записується як f(x1,…, xn) чи f(x), якщо x
представляє (x1,…, xn). У багатьох книгах і
статтях термін часткова функція використовується для позначення функції
з Nn у N, область визначення якої не обов'язково збігається з Nn.
Для нас слово функція означає часткову функцію. Проте при нагоді ми
будемо писати «часткова функция», щоб підкреслити її можливу «не усюди
визначеність». Тотальною функцією з Nn у N ми називаємо
функцію з Nn у N), область визначення якої є всі Nn. l
Ми
затушовуємо розходження між функціями і їхнім значеннями в різних крапках,
особливо у випадку теоретико-числових функцій у двох досить стандартних і
недвозначних ситуаціях. По-перше, ми допускаємо такі фрази як «Нехай f(x1,…,
xn) – функція…», що означає, що f є n-місною функцією.
По-друге, ми часто описуємо функцію в термінах її значення, що задається деякою
формулою. Наприклад, «функція х2» означає «одномісна
функція f, значення якої в кожному х  N є х2»;
аналогічно «функція х + у» означає «двомісна функція», значення якої в
кожній парі (х, у)
N є х2»;
аналогічно «функція х + у» означає «двомісна функція», значення якої в
кожній парі (х, у)  N2 є х+ у.
N2 є х+ у.
Функцію,
тотожно рівну 0 на N, ми позначаємо через 0, і взагалі для т  N функцію N
N функцію N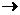 N,
значення якої усюди дорівнює т, ми позначаємо жирним символом т.
N,
значення якої усюди дорівнює т, ми позначаємо жирним символом т.
3.
Відношення і предикати
Якщо А
– множина, то властивість М(х1,…, хn), що
виконується на деяких n-ках з Аn і не виконується (чи
помилкове) на всіх інших n-ках з An, називається п-місним
відношенням, чи предикатом на А.
Наприклад,
властивість х<у є двомісне відношення (чи предикат) на N; 2 < 3
виконується (чи істинно), тоді як 9 < 5 не виконується (чи хибно). Інший
приклад: кожна n-місна функція f з Nn у N приводить до (п
+ 1) – місцевого предиката М (х, у), що задається умовою:
М (x1,…,
хn, у), якщо і тільки якщо f (x1,…, xn)
 у.
у.
Відношення
еквівалентності і порядку. (Читач, не знайомий з цими поняттями, може при
бажанні відкласти читання цього параграфа доти, поки він не буде потрібен в гл. 9.)
У гл. 9 ми зустрінемося із двома спеціальними видами відносин на множині А.
(a)
Бінарне відношення R на множині А називається відношенням
еквівалентності, якщо для всіх х, у, z А
виконуються три наступні властивості:
А
виконуються три наступні властивості:
(i)
(рефлективність) R (х, х);
(іі)
(симетрія) R (х, y)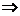 R (у, х);
R (у, х);
(iii)
(транзитивність) якщо R (x, y) і R (у, z), то R (х, z).
Говорячи, що х, y еквівалентні (у деякому спеціальному змісті), ми
маємо на увазі відношення R (х, у). Потім ми визначаємо клас еквівалентності
х як множина {у | R (х, у)}, що складається з всіх елементів,
еквівалентних х.
(b)
Двомісне відношення R на множині А називається частковим
порядком, якщо для всіх х, у, z  A.
A.
(i)
(іррефлексивность) не R (х, х);
(іі)
(транзитивність) якщо R (х, у) і R (y, z), те R (x, z).
Частковий
порядок звичайно позначається символом <, і ми віддаємо перевагу
запису х < у запису < (х, у). Часто визначають частковий
порядок, вводячи спочатку предикат < (позначающий < чи =) із
властивостями:
(i) х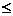 х;
х;
(ii)
якщо x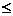 y і у
y і у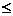 х,
те х=у;
х,
те х=у;
(iii)
відношення 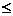 транзитивно, а потім
визначаючи х < у як х
транзитивно, а потім
визначаючи х < у як х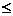 у
и х
у
и х 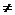 у.
у.
4.
Логічні позначення
Ми
скрізь вживаємо стандартні логічні позначення. Символ 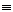 позначає
еквівалентність по визначенню,
позначає
еквівалентність по визначенню, 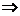 означає логічне
слідування, а
означає логічне
слідування, а 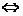 позначає «випливає з».
Символи
позначає «випливає з».
Символи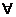 ,
, 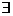 використовуються
в значенні «для всіх» і «існує» відповідно.
використовуються
в значенні «для всіх» і «існує» відповідно.
3. Операторні та
предикатні алгоритми – І
(Рекурсивні
функції на області натуральних чисел N)
Розглянемо математичне визначення [1,2] класів функцій
та предикатів, що вважаються точним аналогом інтуїтивного поняття алгоритму
(взагалі кажучи, часткового).
1. Введемо зчисленні множини символів або послідовностей
символів (слів, ідентифікаторів і т. п.) із довільної конструктивної
множини:
а) індивідні: x, y, z, x0, y0, z0, x1, y1, z1,… xj, yj,
zj,…;
б) функціональні: f, g, h, f0, g0, h0, f1, g1, h1,… fj,
gj, hj,…;
в) предикатні: P, Q, R, P0, Q0, R0, P1, Q1, R1,… Pj, Qj,
Rj,…;
г) константи: a, b, c, a0, b0, c0, a1, b1, c1,… aj, bj,
cj,…;
д) мітки: q, i, j, q0, i0, j0, q1, i1, j1,… qk, ik, jk,…
Кожній функціональному та предикатному символу U
однозначно ставиться у відповідність натуральне число n, яке називається
арністю даного символа. Цей символ позначається через U(n), або U (x1, x2., xn)
та т. п., і називається n-арним символом. Вважається, що ідеалізований
об'єкт – 0-арний функціональний символ U(0) співпадає з символом константи.
Схемою оператора присвоювання
називається вираз виду:
z(i) = f(m) (x(1)., x(m)). (1)
Схемою оператора пересилки
називається вираз виду:
z(k) = y(j) (2)
Схемою прісвоювання константи
називається вираз виду:
z(k) = a, або z(k) = fj(0) (3)
Схемою умови називається вираз
виду:
P(s) (x(1)..x(s)) (4)
Схемою програми
(СП) S називатимемо об'єкт виду
q0 Ф[0] (i0, j0)
q1 Ф[1] (i1, j1)
……………. (5)
qs Ф[s] (is, js)
В (1) Qs = Qs1 u Qs2, де Qs1 = q0,
q1..qs, і
Qs2=i0, j0., is, js – підмножини множин міток. Як
правило, якщо не вказане уточнення, будемо вважати, що qi – qj, якщо i – j, (qi,
qj належать Q1). Мітки із Q1 називаються мітками передачі управління, а мітки
із (Qs – Qs1) – кінцевими мітками.
Для всіх k є [0_s], Ф[k] – це одна із схем
(1) – (4).
Сукупність всіх індивідних змінних СП (5) називається пам
"яттю схеми S. Сукупність константанктних, функціональних,
предикатних символів і пам" яті S називається сигнатурою, або
базисом, схеми S.
Конструкція вигляду
qr Ф[r] (ir, jr)
із (5) називається схемою команди.
Схемою операторного алгоритму (СОА), або схемою
операторної процедури, називається об"єкт виду:
SA = (x1, x2., xn; S;
y), (6)
де x1., xn, y – змінні, S – СП вигляду (5).
Схемою предикатногоо алгоритму (СПА), або схемою
предикатної процедури, називається об"єкт виду:
SP = (x1, x2., xn; S;
q [.t.], q [.f.]), (7)
де x1., xn, – змінні, S – СП вигляду (5), а q
[.t.], q [.f.]) – кінцеві мітки СП S.
Зауважимо, що пам "яттю алгоритмів (6), (7)
називається об" єднання пам"ятті S і змінних x1., xn, y, і x1.,
xn називаються вхідними змінними, а y – вихідною змінною.
Ми визначили СП, СОА і СОП як деякі формальні,
синтаксичні конструкції. Яка ж семантика (сенс) цих конструкцій? Як із них
отримати справжні алгоритми (програми)?
Семантика схем задається за допомогою інтерпретацій.
Інтерпретація схеми алгоритму W задається парою (D, I), де D – множина
довільної природи, а I – це певне відображення, яке: а) кожному символу змінної
z із пам"яті W ставить у відповідність елемент I(z) із множини D; б)
кожному символу константи b із сигнатури W ставить у відповідність елемент I(b)
із D; в) кожному m-арному функціональному f(m) (предикатному P(m)) символу
співставляє, відповідно, всюдиозначені функцію I (f(m)): Dm ->D, або
предикат I (P(m)) ->.t..f.
2. Нижче в данному розділі будемо розглядати тількі
підклас схем алгоритмів KS-1, які містять тільки
два функціональні унарні символи f, g, один константний символ b і один унарний
предикатний символ p. Також обмежимо клас інтерпретацій, поклавши, що в цьому
класі KI-1 D завжди співпадає з множиною натуральних чисел N (D=N), а
відображення I задовольняє наступним вимогам:
1) I(b) = 0;
2) I (f(x)) = I(x) + 1;
I(x) – 1, коли x>0
3) I (g(x)) = I(x) -^ 1 =0 , коли x=0 (8)
t., коли I(x) =0;
4) I (p(x)) = P0 (x)) = *
f., коли I(x) > 0.
5) I(xi) єN для всіх вхідних змінних СОА і
СПА виду (6), (7), і I(y) = 0 для всіх інших змінних із пам'яті
вищезгаданих схем алгоритмів.
Опишемо формально функціонування алгоритму A виду (6).
Нехай M(A) = z1, z2..zn..zm – пам'ять алгоріму A,
де zi = xi при 1<= i <= n, і zm = y. Через
Q(A) позначимо всі мітки A. Станом пам'яті A будемо називати послідовність (a1..am)
натуральних чисел, тобто елемент Nm. Станом (конфігурацією) алгоритму A будемо
називати елемент <q; a1., am> із D(A) = Q & Nm.
Стан <q; a1., am> називається: а) проміжковим,
якщо q – мітка передачи управління; б) кінцевим (заключним), якщо q – кінцева
мітка алгоритму A.
Визначемо функцію переходів F: D(A) –> D(A) алгоритму
A.
1. Коли <q; a1., am> – кінцевий стан, то
F (<q; a1., am>) = <q; a1., am>.
2. Коли <q; a1., am> – проміжковий стан, то
значення F залежить від виду команди qk Ф[k] (ik, jk) в (5).
Якщо Ф[k] має вигляд:
a) zr = zt + 1, то F (<q; a1., am>) =
<q*; b1., bm>, де q* = ik, br = at + 1, а bu = au
для всіх таких u, що u не рівне r;
b) zr = zt -^ 1, то F (<q; a1., am>) =
<q*; b1., bm>, де q* = ik, br = at -^ 1, а bu = au
для всіх таких u, що u не рівне r;
c) zr = 0, то F (<q; a1., am>) =
<q*; b1., bm>, де q* = ik, br = 0, а bu = au для всіх таких
u, що u не рівне r;
d) zr = zt, то F (<q; a1., am>) =
<q*; b1., bm>, де q* = ik, br = at, а bu = au для всіх
таких u, що u не рівне r;
e) P0 (zr), то F (<q; a1., am>) = <q*;
b1., bm>, де bu = au для всіх u (1<= u <= m), а
q* = ir, якщо ar = 0, і q* = jr, якщо ar > 0.
Перейдемо до визначення функції f[A]: Nn –> N, яку
обчислює алгоритм A при інтерпретації I.
По означенню інтерпретації маємо, що початковий стан
пам'яті є I (M(A)) = <a1., an, 0., 0>. Стан c[0] =<q0;
a1., an, 0., 0> називається початковим станом алгоритму A при інтерпретації
I. Скінченна або нескінченна послідовність
T(A) = c[0], c[1]., c[k], c [k+1],… (9)
називається траєкторією (шляхом) алгоритму A при
інтерпретації I (на вході <a1., an>), якщо
F (c[k]) = c [k+1] для всіх k із N.
Зрозуміло, що траєкторія (9) для A будується
конструктивно по програмі цього алгоритму і початковому значенню вхідних
змінних, що задає інтерпретація I.
При послідовному обчисленні станів c[k] за допомогою
функції переходів F можливі два випадки:
1) в траєкторії (9) знайдеться стан с[t] = <q*;
b1., bm> такий, що c[t] – кінцевий стан, а c[0], c[1]., c [t-1] – проміжкові
стани;
2) в траєкторії (9) всі стани проміжкові, тобто
траєкторія T(A) є нескінченною послідовністю станів A.
У першому випадку будемо вважати, що A обчислює значення
f[A] (<a1., an> функції f[A] в точці <a1., an>, i f[A] (<a1., an>)
= bm. Нагадаємо, що bm природнім чином можна інтерпретувати як число, що
знаходиться в вихідній змінній y в стані c[t] алгоритму A, так як, по
припущенню, zm = y.
Якщо в траєкторії (9) всі стани проміжкові, тобто
траєкторія T(A) є нескінченною послідовністю станів A, будемо вважати, що A
циклює в точці <a1., an>, тому значення f[A] (<a1., an> функції
f[A] в точці <a1., an> не визначено, тобто f[A] (<a1., an>) =
@. Іншими словами,
bm, коли T(A) – скінченна f[A] (<a1., an>) =
*
@, коли T(A) – нескінченна (8)
Аналогічно визначається траєкторія і функція переходів
для предикатного алгорітму Aq, і вважається що Aq реалізує предикат;
і q* = q [.t.]; .t., коли T(A)
– скінченна,
P[Aq] (<a1., an>) = * .f., коли T(A) – скінченна,
i
і q* = q [.f.];
@, коли T(A) – нескінченна.
Замінивши у (5) сімволи f, g, b, і p згідно з
інтерпретацією I ми отримаємо програмноподібну структуру, рядки якої будемо
називаті командами. Тому схеми алгоритмів (6) і (7) iз класу KS-1 далі
інтерпретуються, як відповідні алгоритми (програми) iз класу прграм KП-1,
функціонування яких подібно до функціонування програм, що написані на мовах
програмування типу Паскаль, Бейсік і т. п.
А саме:
1) символ «=» у схемах (1) – (3) інтерпретується
як оператор присвоєння;
2) елементи із Qs інтерпретуються аналогічно міткам в
мовах програмування;
3) виконання команди qr x = y + 1 (ir, jr)
інтерпретується як послідовність команд qr: x = y+1; go to ir;
4) виконання команди qr x = y -^1 (ir, jr)
інтерпретується як послідовність команд qr: x = y-^1; go to ir;
5) виконання команди qr x = y (ir, jr)
інтерпретується як послідовність команд qr: x = y; go to ir;
6) виконання команди qr x = 0 (ir, jr)
інтерпретується як послідовність команд qr: x = 0; go to ir;
7) виконання команди qr P0 (x) (ir, jr) інтерпретується
як умова qr: IF P0 (x) THEN go to ir ELSE go to jr.
Як і у більшості мов програмування, оператор «go to ir» при
функціонуванні програми передає управління на команду з міткою ir, а оператор «IF
P0 (x) THEN go to ir ELSE go to jr» передає управлыння
на команду з міткою ir, якщо предикат P0 (x) =.t.
(x = 0), і передає управління на команду з міткою jr, якщо предикат P0 (x)
=.f. (x > 0).
В теорії алгоритмів вважається, що операторні SA
та предикатні SP алгоритми із KS-1 виконуються на вхідних даних із N
абстрактними автоматамиом – багаторегістровими обчислювальними машинами (N-БРМ).
Для кожного алгоритму А ця машіна Ба складається з блоку управління і m
регістрів, де кожний регістр (комірка) Rk може зберігати довілне натуральне
число. Блок управління містить програму Па і забезпечує її виконання по
вищенаведеній схемі. Система команд N-БРМ складається з множини 0, x+1, x-^1,
P0 (0), які можуть виконуватися над вмістом кожного Rk, а також команд
присвоювання, безумовного і умовного переходу, пересилки і запису в регістр.
Часткові або всюдиозначенні k-арні функцію g: Nk –>
N, яка задана на натуральних числах, або предикат P: E* –> T, F, будемо
називати рекурсивною функцією (предикатом), або R-функцією (R-предикатом), якщо
існує програма із класу КП-1 П1g, що обчислює g (P).
Приклади доведення по побудові рекурсивності функцій
наведені у розділі VI данної інструкції.
Як відомо [1,2], згідно до тези Тюрінга-Черча, клас всіх
R-функцій вважаються точним аналогом інтуїтивного поняття алгоритму (взагалі
кажучи, часткового).
3. Аналгічно до класів KS-1 схем алгоритмів і
¶нтерпретацій KI-1 введемо, відпвидно, класи KS-2 і KI-2.
Нехай E = a1., an – деякий алфавит. Через E*
позначимо множину всіх слів в алфавібі E, включаючи однолітерні слова виду 'ai'
і пусте слово e =''.
Введемо на E* деякі стандартні функції і предикати. Якщо
w = x1x2..xm і v = y1y2..yk – слова iз E*, то
а) con (w, v) = wv = x1x2..xmy1y2..yk, con
(e, v) =con (v, e) = v;
б) del(w) = d(w) = x2x3..xm, del(e) =
e;
в) для всіх літер ai із E предикат hai(w) = T
(істино), коли x1 = ai, і hai(w) = F (хибно), коли перша літера
x1 у слові w не дорівнює ai (1 <= i <= m), причому для всіх
i
hai(e) = F.
Якщо а – довільна літера із E*, то через (a^n)
позначається слово, що склдається із n літер a.
Клас схем програм KS-2 містить (n + 1) унарних
функціональних символів fa1, fa2., fan, g, один константний символ b і n
унарних предикатних символів pa1, pa2., pan,
В класі інтерпретацій KI-2 схем із KS-1 множина D завжди
співпадає з множиною E* всіх слів в алфавіті E, а кожне відображення I із KI-2
задовільняє наступним вимогам:
1) I(b) = е;
2) I (fai(x)) = con (I(x), 'ai')= I(x) ai
для всіх літер ai із E;
3) I (g(x)) = del (I(x));
4) I (pai(x)) = hai (I(x)) для всіх літер ai із
E;
5) I(xi) єE* для всіх вхідних змінних СОА
і СПА виду (6), (7), і I(y) = e для всіх інших змінних із пам'яті
вищезгаданих схем алгоритмів.
Замінивши у (5) сімволи fai, g, b і hai згідно з
інтерпретацією I із класу KI-2 ми отримаємо програмноподібну структуру, рядки
якої будемо називаті командами. Тому схеми алгоритмів (6) і (7) iз класу KS-2
далі інтерпретуються, як відповідні алгоритми (програми) iз класу прграм KП-2,
функціонування яких подібно до функціонування програм, що написані на мовах програмування
типу Паскаль, коли ці програми працюють на даних типу string. Ясно, що
функціонуваня команд програм із класу КП-2 аналгічно, з точністю до
інтерпретації символів її схеми, до функціонуваня команд програм із класу КП-1,
яке було описано вище.
Зауважимо також, що по аналогії з N-БРМ БN можна ввести
E-БРМ БE, що реалізує програму із КП-2, а також NE-БРМ БNE. БNE можна
розглядати як «об'єднання» програм ПN i ПE для БN i БE в тому сенсі, що множини
регістрів БN i БE не перетинаються, але вони мають загальний блок управління (i
спільні мітки), в якій поміщена спільна програма ПNE, в яку входять всі
команди, як із ПN так і із ПE.
Часткові або всюдиозначенні функцію g: E*вх –>E*вх,
яка задана на множині слів довільного алфавіту E, або предикат P: E* –> T, F,
будемо називати E – рекурсивною функцією (предикатом), або RE-функцією (RE-предикатом),
якщо існує програма із класу КП-2 П1g, що обчислює g (P).
Як відомо [1], [2], за допомгою кодуючої функції
доводиться, що, в певному сенсі, клас R-функцій (R-предикатів) і клас RE-функцій
(RE-предикатів) є еквівалентні.
Приклади доведення по побудові RE-рекурсивності функцій
і предікатьв наведені далі.
Побудуємо алгоритм, що обчислює функцію
z:= f1 (x, y) = x + y.
x, y! z
|
q10
q11
q12
q13
q14
q15
q16
q17
q18
q19
|
x1 = x (q11, q11)
y1 = y (q12, q12)
z1 = 0 (q13, q13)
P0 (x1) (q16, q14)
z1 = z1 + 1 (q15, q15)
x1 = x1 -^ 1 (q13, q13)
P0 (y1) (q19, q17)
z1 = z1 + 1 (q18, q18)
y1 = y1 -^ 1 (q16, q16)
z = z1 (Я, Я)
|
Побудуємо алгоритм (не оптимальний), що заносить в z
значення функції добутку x i y, тобто z:= f1 (x, y) = x * y.
x, y! Z
|
q20
q21
q22
q23
|
x2 = x (q21, q21)
y2 = y (q22, q22)
z2 = 0 (q23, q23)
P0 (y2) (q25, q10)
|
|
q10
q11
q12
q13
q14
q15
q16
q17
q18
q19
|
x1 = z2 (q11, q11)
y1 = x (q12, q12)
z1 = 0 (q13, q13)
P0 (x1) (q16, q14)
z1 = z1 + 1 (q15, q15)
x1 = x1 -^ 1 (q13, q13)
P0 (y1) (q19, q17)
z1 = z1 + 1 (q18, q18)
y1 = y1 -^ 1 (q16, q16)
z2 = z1 (q24, q24)
|
|
q24
q25
|
z2 = z1 (q23, q23)
z = z2 (Я, Я)
|
Нехай алфавіт Е = a, b. Побудуємо алгоритм, що
обчислює предикат Pe(w), де Pe(w) = T тоді і тільки тоді, коли w є пусте
слово із E*, тобто w = e.
x! q [.t.], q [.f.]
q10 x1 = x (q11, q11)
q11 ha(x1) (q [.f.], q12)
q12 hb(x1) (q [.f.], q [.t.])
Побудуємо алгоритм (не оптимальний), що заносить в z
значення функції con (x, y) = xy, тобто z:= g1 (x, y) = con
(x, y) = = xy для слів із Е = a, b.
x, y! Z
|
q20
q21
q22
|
x2 = x (q21, q21)
y2 = y (q22, q22)
z2 = e (q10, q10)
|
|
q10
q11
q12
|
x1 = y2 (q11, q11)
ha(x1) (q22, q12)
hb(x1) (q22, q28)
|
|
q22
q23
q24
|
ha(y2) (q23, q25)
x2 = con (x2, a) (q24, q24)
y2 = del(y2) (q22, q22)
|
|
q25
q26
q27
q28
|
hb(y2) (q26, q10)
x2 = con (x2, b) (q27, q27)
y2 = del(y2) (q25, q25)
z = x2 (Я, Я)
|
4. Операторні та
предикатні алгоритми -ІІ
(Рекурсивні
функції на областях, що відмінні від N)
Оскільки
БРМ працює тільки з натуральними числами, наше визначення обчислюваності і
можливості розв'язання застосовано тільки до функцій і предикатів від
натуральних чисел. Ці поняття легко поширюються на інші види об'єктів (тобто
цілі числа, поліноми, матриці і т.д.) за допомогою кодування.
Кодуванням області D
об'єктів називається явне й ефективне відображення α: D →N. Ми
будемо говорити, що об'єкт α € D кодується натуральним
числом α (d). Припустимо, що f є функцією з D в D; тоді f природно
кодується функцією f* з N в N, що відображає код кожного об'єкта d €
Dom(f) у код об'єкта f (d). У явному виді це можна записати як
f*=α
· f ·a-1
Тепер
можна поширити визначення Мнр-обчислюваності на область D, рахуючи функцію f
обчислюваною, якщо f*–обчислювана функція натуральних чисел.
Приклад. Розглянемо
область Z. Явне кодування можна задати функцією α, де
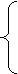 2n, якщо n ³ 0,
2n, якщо n ³ 0,
α-(n)
=
-2n-1,
якщо n < 0.
Тоді
α-1 задається так:
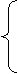 (1/2) m, якщо m парне,
(1/2) m, якщо m парне,
α-1
(m) =
(-1/2)
(m+1), якщо m непарне.
Тепер
розглянемо функцію х-1 на Z; позначаючи цю функ-ю через f,
одержуємо f*:N →N, що задається:
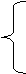 1, якщо x:==0 (тобто х=α(0)),
1, якщо x:==0 (тобто х=α(0)),
f*(x)=
х-2,
якщо х> 0 і х парне (тобто х=а(п), п>0),
х +2, якщо х
непарне (тобто х=α(n), п < 0).
Написання
програми, що обчислює f*, є рутинною вправою; отже, х-1 є
обчислювана функція на Z.
Приведене
вище визначення очевидним образом розширюється на n-місцеві обчислювальні
функції на області D і розв'язні предикати на D.
5.
Алгоритмічні проблеми для L
Нижче
дається огляд нерозв'язних проблем, що виникають у самій теорії
обчислювальності, і обговорюються деякі методи доказу нерозв'язності. Нагадаємо,
що предикат М(х) називається розв'язним, якщо його
характеристична функція, що задається формулою
 1, якщо M(x) правдиве,
1, якщо M(x) правдиве,
Cm
(x) =
0, якщо
M(x) неправдиве
обчислювана.
Це рівносильно твердженню про те, що предикат М (х) рекурсивний Предикат
М (х) називається нерозв'язним, якщо він не є розв'язним. У
літературі використовуються наступні терміни, еквівалентні твердженню про те,
що предикат М (х) розв'язний:
М
(х) рекурсивний,
М
(х) має рекурсивну проблему дозволу,
М
(х) рекурсивно розв'язний,
М
(х) обчислювальний.
Алгоритм,
що обчислює см, називається обчислювальною процедурою, для
M(x).
1.
Нерозв'язні проблеми в теорії обчислюваності
У
більшості випадків докази нерозв'язності ґрунтуються на діагональному методі,
як, наприклад, у наступному важливому прикладі.
1.1.
Теорема. Проблема «x ÎWx»
(чи, що еквівалентно, «функція fx(х) визначена»,
чи «Рx(х)¯», чи «функціяyu(х, х) визначена»)
нерозв'язна.
Доведення. Характеристична
функція цієї проблеми задається наступною формулою:
 1, якщо xÎ Wx
1, якщо xÎ Wx
f(x)=0,
якщо xÏ Wx
Припустимо,
що функція f обчислювана, і приведемо це припущення до протиріччя. Саме за
допомогою діагонального методу ми побудуємо обчислювану функцію g,
таку, що Dom(g)¹Wx(= Dom(фx)), при
всіх х, чого, мабуть, бути не може.
Як
завжди при використанні діагонального методу, ми будемо прагнути до того, щоб
множина Dom(g) відрізнялося від Wx у njxці х. Тому будемо
домагатися того, щоб
x Î Dom (g) Ûx ÏWx
Визначимо
тепер функцію g у такий спосіб:
g(x)= 0, якщо xÏ Wx (тобто
якщо f(x)=0),
не
визначена, якщо xÎ Wx (тобто якщо f(x)=
1).
Оскільки
функція f обчислювана, то (по тезі Черча) обчислювана і функція g, що і
дає необхідне протиріччя. (Більш докладно, оскільки функція g обчислювана,
візьмемо таке т, що g=fm, тоді т Î Wm
Û т Î Dom (g)Ûт Ï Wm,
чого не може бути.)
Отже,
ми робимо висновок, що функція f не є обчислюваною, і, отже, проблема «x ÎWx» нерозв'язна. ÿ
Зауважимо,
що ця теорема зовсім не затверджує, що ми не можемо для будь-якого конкретного
числа а сказати, чи буде визначене значення fa (a). Для
деяких чисел зробити це дуже просто. Наприклад, якщо ми написали програму Р, що
обчислює тотальну функцію, і Р=Рa, то ми відразу знаємо,
що значення fa (a) визначено.
Теорема говорить лише, що не існує єдиного загального методу рішення питання
про те, чи буде fx(х) визначено; іншими
словами, не існує методу, що працює при всіх х.
Простий
наслідок цього результату полягає в наступному.
1.2.
Наслідок. Існує обчислювана функція h, для якої обидві проблеми «x Î Dom(h)» і «х Î Ran(h)» нерозв'язні.
Доведення. Покладемо
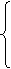 x, якщо xÎ Wx
x, якщо xÎ Wx
h(x)=
не визначена, якщо xÏ Wx
Тоді
в силу тези Черча і обчислюваності універсальної функції yu функція h
обчислювана (більш формально ми маємо h(x)@ x1 (yu(х, х)), а
ця функція обчислювана як результат підстановки). Ясно, що x Î Dom(h)Û xÎ Wx
Ûx Î Ran (h), так що обидві
проблеми «x Î Dom(h)» і «х Î Ran(h)» нерозв'язні.
З
теореми 1.1 виводиться ще одна важлива нерозв'язна проблема:
1.3.
Теорема (проблема зупинки). Проблема «функція фx(у)
визначена» (чи в еквівалентній формі «Рx(y)¯, чи «y Î Wx» нерозв'язна.
Доведення. Міркуючи
неформально, ми відразу бачимо, що якби проблема «функція фx(у)
визначена» була б розв'язна, то була б розв'язна і більш проста проблема «функція
фx(х) визначена», що суперечить теоремі 1.1.
Щоб
провести всі ці міркування більш докладно, розглянемо характеристичну функцію
проблеми^ «функція фх(у) визначена», що має наступний вид:
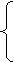 1, якщо фх(у)
визначена
1, якщо фх(у)
визначена
g (x,
y)=
0, якщо фх(у) не визначена
Якби
функція g була обчислювана, то обчислюваною була б і функція f(x)=g
(x, х), але f є характеристична функція проблеми «х Î Wx»
і, отже, не обчислювана в силу теореми 1.1. Отже, функція g не
обчислювана, і тим самим проблема «фx(y) визначена» нерозв'язна.
ÿ
Теорему
1.3 часто інтерпретують як твердження про нерозв'язність проблеми зупинки (для
МНР-программ), у якому говориться про те, що не існує ніякого ефективного
загального методу установити, чи зупиниться деяка конкретна програма, запущена
після введення в неї деякого конкретного набору початкових даних. Зміст цього
твердження для теоретичного програмування очевидний: не існує зовсім загального
методу перевірки програм на наявність у них нескінченних циклів.
Розглянута
в теоремі 1.1 нерозв'язна проблема «х Î Wx»
важлива з кількох причин. Одна з них полягає в тому, що нерозв'язність багатьох
проблем можна довести, показавши, що вони принаймні не простіші, ніж ця. Саме
таким шляхом ми довели, що проблема зупинки (теорема 1.3) нерозв'язна: цей
процес називається зведенням однієї проблеми до іншої.
Узагалі
розглянемо деяку проблему М (х). Часто вдається показати, що рішення
загальної проблеми М (х) привело б до рішення загальної проблеми «х
Î Wx», Тоді говорять, що
проблема «х Î Wx»
зводиться до проблеми М (х). Іншими словами, якщо мається дозволяюча
процедура для проблеми М (x), то ми можемо дати і дозволяючу процедуру
для проблеми «х Î Wx».
Таким чином, з можливості розв'язання М(х) випливає можливість
розв'язання «х Î Wx»,
звідки ми негайно робимо висновок, що М (х) нерозв'язна.
Для
зведення проблеми «х Î Wx»
до інших проблем часто використовується s-m-n-теорема, як показує, наприклад,
доведення наступного результату.
1.4.
Теорема. Проблема «фx=0» нерозв'язна.
Доведення. Розглянемо
функцію f, визначену формулою
 0, якщо х Î Wx
0, якщо х Î Wx
f (x,
y)=
не визначена, якщо x Ï Wx
Цю
функцію ми ввели для того, щоб далі скористатися s-m-n-теоремою. Тим самим ми
розглядаємо х як параметр, і нас цікавлять функції gx,
такі, що gx(y)@ f (x, у). При цьому ми
вибрали f так, що gx=0Ûх Î Wx.
Теза
Черча (чи підстановка з використанням 0 і yu) показує, що
функція f обчислювана. Тому існує тотальна обчислювана функція k(x),
що дається s-m-n-теоремо., така, що f (x, у)@fk(x); тобто fk(x)=gx.
Таким чином, по визначенню
Отже,
питання про те, чи вірно, що х Î Wx,
можна вирішити, відповівши спочатку на питання: чи вірно, що fk(x)=0? Тим
самим ми звели загальну проблему «х Î Wx»
до загальної проблеми «фx=0»; оскільки перша з них нерозв'язна, те
нерозв'язна і друга, що і було потрібно довести.
У
зв'язку з тим що це перший приклад подібного роду, що зустрівся нам, розглянемо
останню частину нашого міркування більш докладно. Нехай g-характеристична
функція проблеми «фx=0», тобто
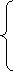 1, якщо фx=0
1, якщо фx=0
g(x)=
0, якщо фx¹0
Припустимо,
що функція g обчислювана. Тоді обчислюваною буде і функція h (х)
= g (k (х)). У той же час співвідношення (*) дає
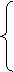 1, якщо фk(x)=0,
тобто xÎ Wx,
1, якщо фk(x)=0,
тобто xÎ Wx,
h(x)=
0, якщо фk(x)¹0, тобто xÏ Wx.
Тим
самим у силу теореми 1.1 функція h не є обчислюваною. Стало бути, і
функція g не є обчислюваною, так що проблема «фx=0»
нерозв'язна. ÿ
Теорема
1.4 показує, що в області перевірки правильності комп'ютерних програм є
принципові обмеження. У ній говориться про те, що не може бути зовсім
загального ефективного методу здійснити перевірку того, чи буде програма
обчислювати нульову функцію. Трохи змінивши доведення теореми 1.4, можна
переконатися в тім, що те ж саме справедливо і для будь-якої іншої конкретної
обчислюваної функції (див. нижче впр. 1.8 (i)).
Простий
наслідок теореми 1.4 показує, що питання про те, чи обчислюють дві програми ту
саму одномісну функцію, нерозв'язне. Зміст цього результату для теоретичного
програмування також очевидний.
1.5.
Наслідок. Проблема «фx=фy» нерозв'язна.
Доведення. Легко
переконатися в тому, що ця проблема складніша проблеми «фx=0». Нехай
с – таке число, що фс=0. Якщо f (x, y) – характеристична функція
проблеми фx = фу, то функція g (x)=f (х, с) є
характеристична функція проблеми «фx=0». По теоремі 1.4 функція g
необчислювана, так що необчислювана і функція f. Отже, проблема «фx=фy»
нерозв'язна.
У
наступних результатах ми знову скористаємося s-m-n-теоремою для зведення
проблеми «х Î Wx».
1.6.
Теорема. Нехай c – довільне число. Наступні проблеми нерозв'язні.
(а)
(Проблема входу) «c Î Wx»
(чи в еквівалентному формулюванні «Рx (с)¯», чи «c Î Dom (фx)»);
(b)
(Проблема виходу) «c Î Ex»
(чи в еквівалентному формулюванні «с Î Ran (фx)»).
Доведення. Ми можемо звести
проблему «х Î Wx» до обох
цих проблем одночасно. Розглянемо функцію f (х, у), визначену в такий
спосіб:
y, якщо х Î Wx
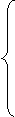 f (x, y)=
f (x, y)=
не визначена в протилежному випадку
(Маючи
на увазі використовувати s-m-n-теорему, ми будемо розглядати функції gx,
для яких gx(y)@ f (x, у). Функцію f ми
вибрали таким чином, що c Î Dom (gx)Û х Î Wx
Ûc Î Ran(gx).)
У силу тези Черча функція f обчислювана, так що s-m-n-теорема дає
тотальну обчислювану функцію k, таку, що f (х, у)@ фk(x)(y).
З визначення f ми бачимо, що
x Î WxÞWk(x)=Ek(x)=N
так
що c Î Wk(x) і c Î Ek(x),і
x Ï WxÞWk(x)=Ek(x)=Æ
так
що c Ï Wk(x) і c Ï Ek(x).
Тим самим ми звели проблему «x Î Wx» до кожної з
проблем «c Î Wx » і «c Î Ex «.
Завершуючи
Доведення пункту (а) більш докладно, ми бачимо, що якщо g-характеристична
функція проблеми «c Î Wx », то
 1, якщо x Î Wx,
1, якщо x Î Wx,
g (k(x))=
0, якщо x Ï Wx
Ця
функція не є обчислюваною (теорема 1.1), так що функція g теж не може
бути обчислюваною. Отже, проблема «c Î Wx » нерозв'язна.
Докладне
доведення пункту (Ь) проводиться аналогічно. ÿ
Ми
закінчимо цей параграф одним дуже загальним результатом про нерозв'язність, з
якого негайно випливають теореми 1.4 і 1.6. При цьому ми знову скористаємося
для зведення проблеми «х Î Wx »
s-m-n-теоремою.
1.7.
Теорема (теорема Райса). Нехай ВÍ b1 і
B¹ Æ, b1.
Тоді проблема «фx Î B» нерозв'язна.
Доведення. Співвідношення
для розв'язних множин (теорема 2–4.7) показують, що проблема «фx Î B» розв'язна тоді і
тільки тоді, коли розв'язна проблема «фx Î b1 \ B». Тому
без втрати загальності ми можемо вважати, що ніде не визначена функція fÆ не належить B
(якщо це не так, то твердження можна довести для b1 \ B).
Виберемо
деяку функцію g Î B. Розглянемо
функцію f (x, у), що задається так:
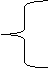 g(y), якщо x Î Wx,
g(y), якщо x Î Wx,
f (x,
y)@
не визначена, якщо x Ï Wx.
Користаючись
s-m-n-теоремою, ми одержуємо тотальну обчислювану функцію k (x), таку,
що f (x, у) @ фk(x) (y),). Таким чином, ми
бачимо, що
x Î Wx Þ фk(x)
=g, тобто фk(x) Î B
x Ï Wx Þ фk(x)
=fÆ, тобто фk(x) Ï B
Це
значить, що за допомогою обчислюваної функції k ми звели проблему «х Î Wx » до проблеми
«фх
Î В». Тепер уже
стандартним чином можна покласти, що проблема «фх Î В» нерозв'язна.
Теорема
1.4, наприклад, негайно випливає з теореми Райса, якщо взяти В ={0}, а
теорема 1.6 (а) – якщо взяти В={g Î b1:c Î Dom(g)}. Аналогічно можна
скористатися теоремою Райса і у наступних вправах.
1.8.
Вправи.
1.
Покажіть, що наступні проблеми нерозв'язні.
(a)
«х Î Ех «. (Указівка.
Скористайтеся діагональним методом чи зведіть до цієї проблеми проблему
«x
Î Wx» за допомогою s –
m- n – теореми.)
(b) «Wx=Wy
«. (Указівка. Зведіть до цієї проблеми проблему «функція фx
тотальна».)
(c) «фx(х)=0».
(d) «фx(y)=0».
(e) «х
Î Еу «.
(f)
«функція фx тотальна і постійна».
(g) «Wx=Æ».
(h)
«множина Еx нескінченна».
(i) «фх=g»,
де g є будь-яка фіксована обчислювана функція.
2.
Покажіть, що не існує тотальної обчислюваної функції f (x, у), що
володіє наступними властивістями: якщо програма Рх(у)
зупиняється, те це відбувається за f (x, у) чи менше кроків (Указівка.
Покажіть, що якби така функція існувала, те проблема зупинки була б
розв'язна.)
Можливість
розв'язання і нерозв'язання в інших областях математики. У багатьох
областях математики виникають проблеми загального характеру, для яких має сенс
неформальне поняття можливості розв'язання. Звичайно такі проблеми стосуються
кінцевих об'єктів деякої конкретної області. У цьому випадку поняттю можливості
розв'язання тієї чи іншої властивості, що стосується цих об'єктів, можна надати
точний зміст, використовуючи придатне кодування натуральними числами.
Виявленню
розв'язних і нерозв'язних проблем у самих різних математичних ситуаціях
присвячено багато досліджень.
6. Дані і знання. Логіка висловлень (ЛВ) в
представленні знань
1.
Логіка висловлень (пропозиційна логіка) [1] – одна з базових теорій
математичної логіки, на якій базуються більш складні формальні логіки.
Алфавіт
логіки висловлень (ЛВ) складається зі зчисленної множини елементарних висловлень,
які позначуються літерами (можливо, з індексами) і 5 логічних операцій: заперечення
(^), кон’юнкції (/\, або &), диз’юнкції (\/), імплікації (->) і
тотожності, еквівалетності (<->), які задаються скінченими таблицями
істинності.
Як
відомо, кожне висловлення може мати значення істинно (позначається Т, 1), або
хибно (позначається F, 0).
Алфавіт
висловлень дає змогу будувати складні висловлення (формулу) із простіших за
допомогою логічних операцій [1] по наступній рекурсивній схемі, а саме,
формулами ЛВ є тільки наступні конструкції:
– кожне
висловлення є формулою;
– якщо
А і В є формули, то ^A, (A/\B), (A\/B), (A -> B) i (Aя2=я0B) – є формулами.
Формули
задають синтаксис мови ЛВ. А який сенс, семантика цієї мови?
Вона задається
за допомогою інтерпретацій. Інтерпретація – це відображення I, що зпівставляє кожному
елементарному висловленню р деяке значення істинності. Інтерпретацію I, що задана
на множині елементарних висловлень, природнім чином можна продовжити на множину
формул за допомогою таблиць істинності. Інтерпретація, при якій істиносне значення
формули А є істинно, називається моделлю цієї формули.
Літера,
або літерал – це елементарне висловлення р або його заперечення ^p. Літери р і
^р є протилежні.
Формула
ЛВ називається виконуваною, якщо вона допускає деяку модель, тобто її можна
інтерпретувати із значенням Т.
Формула
ЛВ А називається суперечністю (не виконуваною), якщо А = F для всіх моделей А
(наприклад, (р/\^p).
Формула
ЛВ називається тавтологією, якщо вона істина при всіх інтерпретаціях (на всіх
моделях). Відмітимо, що заперечення тавтології є суперечність.
2.
Нехай, Е – множина формул ЛВ. Формула А є наслідком (логічним) з Е (позначення,
Е (= А), якщо на всіх моделях, на яких істині всі формули з Е, істина також
формула А. Ясно, що тавтологія є наслідком із пустої множини формул ЛВ.
Легко
довести [1], що мають місце:
Твердження
1. Нехай, Е = {H1, H2,… Hn} є множиною формул ЛВ.
Формула
А є наслідком (логічним) з Е (E (= A) тоді і тільки тоді, коли імплікація:
(H1/\H2/\…/\Hn)
-> A
є
тавтологією. Прямим наслідком із твердження 1 є
Твердження
2. Нехай, Е = {H1, H2..Hn} є множиною формул ЛВ.
Формула
А є наслідком (логічним) з Е тоді і тільки тоді, коли формула
(H1/\H2/\…/\Hn/\^A)
є
суперечністю.
Диз’юнктом
називається диз’юнкція скінченного числа літералів, тобто формула виду
(L1\/L2\/..\/Lm).
Її
часто записують у «скороченому» вигляді як послідовність літералів: {L1., Lm}.Пустий
диз’юнкт – єдиний диз’юнкт, що не виконується, і його позначають через Л.
Кон’юктивною
нормальною формою (КНФ) називається кон’юнкція скінченої кількості диз’юнктів.
Теорема
1. Довільна формула ЛВ має логічно еквівалентну їй КНФ.
Наступний
алгоритм нормалізації формул ЛВ дає доведення теореми 1.
Етап
1. Спочатку замінюємо (А<->В) на ((А->B)/\(B->A)), а потім
заміняємо (U->V) на (^U\/V). Це робиться для виключення операцій <-> і
->.
Етап
2. Необхідну кількість раз застосовуються перетворення на основі законів де
Моргана:
^(X/\Y)
==> (^X\/^Y), ^(X\/Y) ==> (^X/\^Y).
Символ
==> означає «замінити на». В цій заміні подвійні заперечення елімінуються,
тобто
^^X
==> X.
На цій
стадії операція заперечення залишається тілки безпосередньо перед
висловленнями.
Етап
3. необхідну кількість разів застосовуються правила перетворень, що виведені із
законів дистрибутивності:
X \/
(Y /\ Z) ==> (X \/ Y) /\ (X \/ Z)
(X /\
Y) \/ Z ==> (X \/ Z) /\ (Y \/ Z).
Етап
4. Диз’юнкти, що містять протилежні літерали (тобто висловлення і його заперечення),
є тавтологіями і можуть бути еліміновані. Також елімінуються повторення
літералів у межах одного ж і того диз’юнкта.
Формула,
що отримується в кінці четвертого етапу, і є КНФ, яка еквівалентна вихідній
формулі ЛВ.
Відмітимо,
що диз’юнкт є тавтологією тоді і тільки тоді, коли він містить пару протилежних
літералів. КНФ є тавтологією тоді і тільки тоді, коли всі її диз’юнкти – тавтології.
Єдиним
не виконуваним диз’юнктом є пустий диз’юнкт Л.
3. Не
існує загального ефективного критерію для перевірки виконуваності КНФ. Але
існує зручний метод для виявлення не виконуваності множини диз’юнктів. Дійсно, множина
диз’юнктів є не виконувані тоді і тілки тоді, коли пустий диз’юнкт Л є логічним
наслідком із неї. Таким чином, не виконуваність множини S можна перевірити,
породжуючи логічні наслідки з S, поки не отримаємо пустий диз’юнкт. Для цього
використовується наступна схема міркувань.
Припустимо,
що дві формули (A \/ X) i (B \/ ^X) – істині. Якщо Х також істина, то звідси випливає,
що B істина. Навпаки, якщо Х хибна, то А істина, тобто отримується правило
{(A
\/ X), (B \/ ^X)} [= A \/ B,
яке
можна записати у вигляді
{^X
-> A, X -> B} [= A \/ B. Зокрема, якщо Х – висловлення, а A i B – диз’юнкти,
то правило називається правилом резолюції.
Твердження
3. Нехай s1 i s2 – диз’юнкти КНФ S. Якщо літерал р входить у s1 і ^p – у s2, то
диз’юнкт
r =
(s1\{p}) \/ (s2\{^p})
є
логічним наслідком КНФ S.
Тут
через si\{L} позначається диз’юнкт, що отримується з si вилученням літералу L. Диз’юнкт
r називається резольвентою диз’юнктів s1 i s2.
Твердження
4. Нормальні форми S i (S /\ r) еквівалентні.
Доведення
невиконувансті формул дуже важливо для роботи із знаннями. Воно широко
використовується в логічному програмуванні. З твердження 3 і 4 випливає наступний
алгоритм – метод резолюцій для доведення того, що КНФ S є суперечністю.
Метод
резолюцій
Крок
1. Якщо Л належить S, то КНФ S є суперечністю, і алгоритм зупиняється.
Крок
2. Вибираються довільні L, s1, s2 такі, що літерал L входить в диз’юнкт s1, а
^L входить у s2.
Крок
3. Обчислюється резольвента r.
Крок
4. КНФ S замінюється на КНФ S' = S /\ r, і повертаються на крок 1. Вибираються
довільні L, s1, s2 такі, що літерал L входить в диз’юнкт s1, а ^L входить у s2.
Твердження
5. Якщо нормальна форма S є невикнуваною формулою, тобто суперечністю, то цей
факт завжди можна виявити за допомогою метода резолюцій.
1.
Необхідно побудувати кон’юктивну нормальну форму для формули А логіки висловлень,
де
A = (p
-> (q -> r)) -> ((p /\ s) -> r).
Використаємо
алгоритм із розділу 1.2. Кожна з нижченаведених формул еквівалентна А.
Етап
1 (виключення імплікацій).
(p
-> (q -> r)) -> ((p /\ s) -> r),
^ (p
-> (q -> r)) \/ ((p /\ s) -> r),
^ (^p
\/ (q -> r)) \/ (^(p /\ s) \/ r),
^ (^p
\/ (^q \/r)) \/ (^(p /\ s) \/ r),
Етап
2.
(^ ^p
/\ ^ (^q \/r)) \/ ((^p \/ ^s) \/ r),
(^ ^p
/\ (^ ^q /\ ^r)) \/ ((^p \/ ^s) \/ r),
(p /\
(q /\ ^r)) \/ ((^p \/ ^s) \/ r).
Етап
3.
a) (p
\/ ((^p \/ ^s) \/ r)) /\ ((q /\ ^r) \/ \/ ((^p \/ ^s)
\/ r))
b) (p
\/ (^p \/ ^s) \/ r)) /\ /\ (q \/ (^p \/ ^s) \/ r) /\
(^r
\/ (^p \/ ^s) \/r);
c) (p
\/ ^p \/ ^s \/ r) /\ /\ (q \/ ^p \/ ^s \/ r) /\ (^r
\/ ^p
\/ ^s \/ r);
d) T
/\ (q \/ ^p \/ ^s \/ r) /\ T;
e) (q
\/ ^p \/ ^s \/ r).
Ми отримали,
що КНФ В = (q \/ ^p \/ ^s \/ r) формули А складається з одного диз’юнкта.
Приклад
2.
Необхідно перевірити за допомогою метода резолюцій, чи є КНФ S суперечністю, де
S = {p
\/q, p /\ r, ^q \/ ^r, ^p}.
Диз’юнкти
зручно перенумерувати. Отримаємо список:
1. p
\/q
2. p
\/ r
3. ^q
\/ ^r
4. ^p
Далі
обчислюються резольвенти і додаються до S. У нижченаведеному списку кожний диз’юнкт
– резольвента деяких попередніх диз’юнктів. Номера їх наводяться з права від
відповідної резольвенти
5. p
\/ ^r 1,3
6. q 1,4
7. p
\/ ^q 2,3
8. r 2,4
9. p 2,5
10.
^r 3,6
11.
^q 3,8
12.
^r 4,5
13.
^q 4,7
14. Л
4,9
Отримали,
що із КНФ S виводиться пустий диз’юнкт Л, тобто S є суперечністю (не
виконуваною формулою).
7.
Логіка предикатів (ЛП) в представленні знань
(Теорема про
нерозв'язність числення предикатів)
Найпростішою
логічною системою, у якій знаходять висвітлення деякі аспекти математичного
мислення, є числення висловлень. У цьому численні складні твердження
будуються з деяких основних висловлень за допомогою символів, що позначають
логічні зв'язки «не», «і», «чи» і «волоче». Досить легко переконатися в тому,
що якщо числення висловлень визначене досить акуратно, то воно розв'язне.
Це означає, що існує ефективна процедура рішення питання про те, чи є те чи
інше твердження цього числення (тотожно) істинним, тобто справедливим у
всіх можливих ситуаціях. Алгоритм цього дається методом істиннісних таблиць,
добре знайомим багатьом читачам.
Більш
широкими можливостями, ніж числення висловлень, володіє логічна система, що
називається численням предикатів (першого порядку). мовою цього числення
можна формалізувати значну частину всієї математики. Основні твердження в ньому
формуються із символів, що представляють індивідуальні об'єкти (чи
елементи), і предикатів і функцій на них. Складні твердження будуються з
основних з використанням логічних символів числення висловлень, а також
символів " і $.
Мається
точне поняття доведення твердження числення предикатів, причому твердження
доводиться тоді і тільки тоді, коли воно істинно. У 1936 році Черч показав, що
доведеність (і, отже, істинність) у численні предикатів нерозв'язна на
відміну від більш простого пропозиціонального числення. (Гільберт вважав цей
результат самим фундаментальної результатом, що стосується нерозв'язності, у
всій математиці.)
Просте
доведення нерозв'язності проблеми істинності можна дати з використанням МНР,
хоча це вимагає деякого знайомства з численням предикатів. Читачу, що не
знайомий з початками логіки предикатів, ми радимо пропустити приведений нижче
зразок доведення.
5.1.
Теорема. Проблема істинності числення предикатів першого порядку
нерозв'язна.
Доведення. (Тим, хто не
знайомий з численням предикатів, рекомендується пропустити.)
Нехай
Р – деяка програма в стандартному виді, що містить команди I1,…,
Is, і нехай u=r(P) (визначення див.
§ 2 р. 2). Ми будемо використовувати наступні позначення символів
числення предикатів:
O –
індивідний символ,
' –
символ одномісної функції (значення якої на х дорівнює х'),
R-символ
(u+1) – місного відношення,
x1,
x2,…, xa, у – символи індивідних змінних.
Далі,
для будь-якої команди Ii, можна записати твердження числення
предикатів ti, що описує
результат виконання команди Ii. При цьому ми використовуємо
символ Ù для позначення зв'язки «і» і символ ® для позначення
імплікації. Твердження ti, визначається в
такий спосіб:
(a)
якщо Ii=Z(n), тo ti, є твердження
"x1 … "xu: R
(x1, …, xn, …, xu, i)®R (x1,
…, O, …, xu, i ¢)
(b)
якщо Ii=S(n), то ti, є твердження
"x1 … "xu: R
(x1, …, xn, …, xu, i)®R (x1,
…, xn¢, …, xu, i ¢)
(c)
якщо Ii=T (m, n), тo ti, є твердження
"x1 … "xu: R
(x1, …, xn, …, xu, i)®R (x1,
…, xm, …, xu, i¢)
(d)
якщо Ii=J (m, n, q), тo ti, є твердження
"x1 … "xu: R
(x1, …, xu, i)®((xm =
xn ®R(x1, …, xu,
q))Ù(xm ¹ xn ®R(x1,
…, xu, i¢)))
Нехай
тепер для будь-якого а Î N символ  sa позначає
твердження.
sa позначає
твердження.
(t0Ùt1Ù…ÙtsÙ R (a, O,… O, 1))®$x1 … $xu R(x1,
…, xu, s+1)
де t0 є твердження "x"y((х'=у® x=y) Ù x¢¹O). (Це гарантує
нам, що при будь-якій інтерпретації з т, n
Î N і m=n випливає, що т=п.)
Твердження
R (a, O,…, О, 1) відповідає вихідному стану
|
а
|
0
|
0
|
…;
|
наступна команда Ii
|
а
будь-яке твердження R(x1,…, хu, s +1) відповідає зупинці
(оскільки немає команди Is+1). Ми покажемо, що
(*) Р
(а)¯Ûsa істинно.
Припустимо
спочатку, що Р(а)¯ і що мається структура,
у якій твердження t0,…, ts, і R (a, O,…,
O, 1) виконуються. За допомогою тверджень t0,…, ts, ми одержуємо,
що кожне з тверджень R(r1,…. ru, k),
що відповідають
послідовним станам обчислення, також виконується. Зрештою ми приходимо до того, що для деяких b1,…,
bu Î N виконується твердження
про зупинку R(b1,…, bu, s+1) і, отже, виконується
твердження $x1 …$xu R(x1,…,
xu, s+1). Таким чином, твердження sa істинно.
Знову,
якщо твердження sa істинно, то воно
виконується, зокрема, у структурі N, причому предикатний символ R
інтерпретується як предикат Ra, для якого
Ra(a1,…, аu,
k)ºНа деякому етапі обчислення Р (а) у
регістрах містяться числа а1, a2,…, au,
0, 0,…, а наступна команда є Ik.
Тоді
твердження t0,…, ts, і R (a, O,…,
O, 1) також виконуються в цій структурі, а отже, і твердження $x1 …$xu R(x1,…,
xu, s+1). Звідси Р(а)¯.
Якщо
в якості Р узяти програму, що обчислює функцію yu (x, х),
то співвідношення еквівалентності (*) зводить проблему «x Î Wx» до проблеми «s істинно». Звідси
випливає, що остання проблема нерозв'язна. ÿ
Математична
логіка буяє результатами, що стосуються можливості розв'язання і
нерозв'язності. Звичайно мова йде про задачі, у яких необхідно установити, чи
буде деяке твердження істинним у всіх математичних структурах визначеного типу.
Наприклад, було показано, що проблема «s є твердження, істинне
для всіх груп» є нерозв'язною (s тут є твердження мовою
числення предикатів першого порядку, що відповідає теорії груп), тоді як
проблема «s є твердження, істинне для всіх абелевих груп»
розв'язна. (При цьому прийнято говорити, що теорія груп першого порядку нерозв'язна,
у той час як теорія абелевых груп першого порядку розв'язна.) Як було
показано Тарським [1951], проблема «твердження s істинне в полі
дійсних чисел» є розв'язної. З іншого боку, як ми побачимо в р. 8, багато
проблем, зв'язаних з формалізацією арифметики натуральних чисел, нерозв'язні.
З
іншими прикладами, а також з доведеннями багатьох результатів, що стосуються
можливості розв'язання і нерозв'язності в математичній логіці, читач може
ознайомитися в книгах Тарського, Мостовського і Робінсона [1953] чи Булоса і
Джефрі [1974], а також Єршова [1981]*.
Размещено
на