Проблема дискретного логарифмування
Проблема дискретного
логарифмування
В пошуках криптографічних
алгоритмів з відкритим розповсюдженням ключів з експоненціальною складністю
криптоаналізу спеціалісти зупинилися на криптографічних перетвореннях, що
виконуються в групі точок ЕК.
Відповідно до прогнозів ці
перетворення ще довго забезпечуватимуть необхідний рівень стійкості. Розглянемо
основні задачі криптоаналізу для систем, в яких перетворення здійснюються в
групі точок ЕК, методи їх розв'язання та дамо оцінку стійкості для відомих нам
методів криптоаналізу.
Під час аналізу стійкості
необхідно розглянути дві проблеми стійкості – розв’язання задачі дискретного
логарифму та задачі Діффі-Хеллмана.
Проблема дискретного логарифму
формується у наступному вигляді. Нехай задано точку 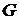 на еліптичній кривій
на еліптичній кривій 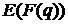 , де
, де 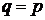 (
(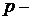 просте число) або
просте число) або 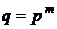 (
(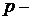 просте число,
просте число, 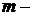 натуральне,
натуральне, 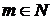 ). Відомо також значення відкритого ключа
). Відомо також значення відкритого ключа 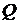 , причому
, причому
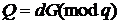 . (1)
. (1)
Необхідно знайти конфіденційний
(особистий ) ключ  .
.
Проблема Діффі – Хеллмана
формується у наступному вигляді. Нехай дано ЕК 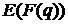 , відомо значення точки
, відомо значення точки 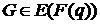 , а також відкритий ключ
, а також відкритий ключ  . Необхідно знайти загальний
секрет
. Необхідно знайти загальний
секрет
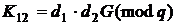 , (2)
, (2)
де 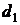 та
та 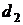 – особисті ключі відповідно першого та другого
користувачів.
– особисті ключі відповідно першого та другого
користувачів.
Насьогодні для аналізу стійкості
та проведення криптоаналізу знайшли розповсюдження декілька методів Полларда - 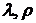 та оптимальний
та оптимальний  .
.
Поллард запропонував замість
детерміністського псевдоймовірнісний алгоритм розв’язання  в полі
в полі 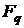 .
.
Це дозволило істотно знизити
вимоги до обсягу пам'яті при практично тій же стійкості алгоритму. Ідея методу
заснована на випадковому пошуку двох співпадаючих точок серед точок криптосистеми.
У теорії ймовірностей добре відомі
задачі про випадкові блукання. Одна із задач ставиться так. Є 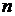 ящиків і
ящиків і 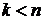 куль, які випадково розміщені по ящиках.
куль, які випадково розміщені по ящиках.
Процедура закінчується при першому
влученні кулі у вже зайнятий ящик. Потрібно визначити медіану розподілу
ймовірностей 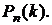
Більш простою моделлю є задача про
співпадаючі дні народження. Якщо 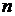 - число днів
у році, то скільки чоловік
- число днів
у році, то скільки чоловік 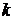 з рівноймовірними днями народження в році
потрібно відібрати, щоб з імовірністю
з рівноймовірними днями народження в році
потрібно відібрати, щоб з імовірністю 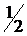 дні народження хоча б двох чоловік
збіглися?
дні народження хоча б двох чоловік
збіглися?
Очевидно, що ймовірність такої
події дорівнює

При 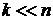 неважко отримати наближене значення цієї
імовірності
неважко отримати наближене значення цієї
імовірності

Приймаючи  , отримаємо оцінку числа
, отримаємо оцінку числа 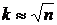 . Інакше кажучи, щоб при випадковому
переборі великої множини із
. Інакше кажучи, щоб при випадковому
переборі великої множини із 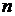 чисел з імовірністю 50% двічі з'явилося те
саме число, буде потрібно в середньому порядку
чисел з імовірністю 50% двічі з'явилося те
саме число, буде потрібно в середньому порядку 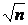 спроб. Збіг елементів або точок в аналізі
прийнято називати колізією. Нехай
спроб. Збіг елементів або точок в аналізі
прийнято називати колізією. Нехай 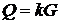 , де генератор
, де генератор 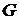 криптосистеми має великий простий порядок
криптосистеми має великий простий порядок 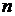 . Алгоритм
. Алгоритм  - методу в застосуванні до еліптичних
кривих полягає в послідовному обчисленні точок
- методу в застосуванні до еліптичних
кривих полягає в послідовному обчисленні точок

де  - якась міра
координати
- якась міра
координати  точки
точки 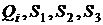 - три рівноймовірні області, у які може потрапити ця
міра. Виберемо випадкові значення
- три рівноймовірні області, у які може потрапити ця
міра. Виберемо випадкові значення 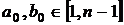 й визначимо початкову точку як
й визначимо початкову точку як  Ітераційна послідовність обчислень
дає послідовність
Ітераційна послідовність обчислень
дає послідовність 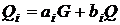 ,
таку що
,
таку що

На кожному кроці обчислене
значення  порівнюється
з попереднім аж до збігу (колізії)
порівнюється
з попереднім аж до збігу (колізії)  або
або
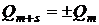 .
.
Алгоритм разом з колізією дозволяє
скласти рівняння
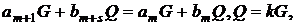
з якого визначається значення
дискретного логарифма
 .
.
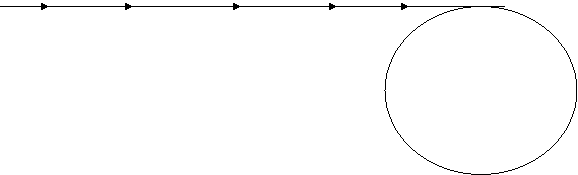
Походження терміна ( -метод) пов'язане із графічною
інтерпретацією алгоритму, зображеної на рис. 1. При замиканні петлі виникає
періодичний цикл.
-метод) пов'язане із графічною
інтерпретацією алгоритму, зображеної на рис. 1. При замиканні петлі виникає
періодичний цикл.
Це обумовлено детермінованістю
алгоритму. Його називають імовірнісним лише у зв'язку з непередбачуваністю
шляху, за яким виконується одне із трьох обчислень.
Q0 Q1 Q2
Qm
 Qm+1
Qm+1
 Qm+s-1
Qm+s-1
Рисунок 1 - Графічна інтерпретація  -методу Полларда
-методу Полларда
Реалізація методу пов'язана з
нарощуванням пам'яті, у яку записуються 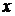 -координати точок, що
-координати точок, що 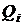 обчислюють. У міру збільшення порядку
обчислюють. У міру збільшення порядку 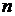 криптосистеми він незабаром
стає практично нереалізованим. Позбутися від цього недоліку вдається за
допомогою методу Флойда. Ідея методу проста й елегантна.
криптосистеми він незабаром
стає практично нереалізованим. Позбутися від цього недоліку вдається за
допомогою методу Флойда. Ідея методу проста й елегантна.
На циферблаті секундна стрілка
завжди обганяє хвилинну, а хвилинна - годинну.
При влученні всередину петлі в  -методі Полларда якась точка
-методі Полларда якась точка 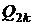 наздоганяє точку
наздоганяє точку  (колізія
(колізія 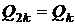 ), що дає рішення ECDLP. У такий спосіб
замість порівняння чергової обчисленої точки з усіма попередніми достатньо у пам'яті
зберегти для порівняння лише дві точки:
), що дає рішення ECDLP. У такий спосіб
замість порівняння чергової обчисленої точки з усіма попередніми достатньо у пам'яті
зберегти для порівняння лише дві точки: 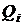 і
і 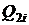 .
.
Точка колізії при цьому зрушується
усередину петлі на відстань, що не перевищує половини довжини петлі. Тим самим
відбувається обмін необхідної пам'яті на час обчислень.
Кожен цикл у методі Флойда вимагає
обчислення трьох точок відповідно до алгоритму й порівняння двох з них. Вихідні
дані – точки 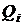 й
й 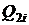 , обчислені в попередньому
циклі. Тоді на їхній основі розраховуються точки
, обчислені в попередньому
циклі. Тоді на їхній основі розраховуються точки  й
й  і рівняються
і рівняються 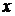 - координати першої й останньої точок. При
їхньому збігу має місце колізія
- координати першої й останньої точок. При
їхньому збігу має місце колізія 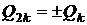 , де знак визначається з порівняння
, де знак визначається з порівняння  - координат обчислених
точок.
- координат обчислених
точок.
Найпростіша ілюстрація цього
методу - спрощений алгоритм із обчисленням 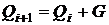 . Колізія на
. Колізія на  -му циклі
-му циклі 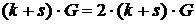 відразу дає розв’язання дискретного логарифму
відразу дає розв’язання дискретного логарифму
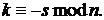
По суті це прямий метод визначення
дискретного логарифму з експоненційною складністю 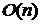 .
.
В іншому окремому випадку
алгоритму маємо
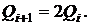
Колізія на  -му кроці призведе до рівняння
-му кроці призведе до рівняння

або 
Воно не має розв'язку 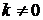 . Якщо модернізувати
алгоритм так, що на кожній ітерації порівнювати точки
. Якщо модернізувати
алгоритм так, що на кожній ітерації порівнювати точки 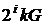 й генератор
й генератор 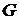 , то при виконанні
, то при виконанні  можна отримати розв’язання
можна отримати розв’язання 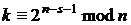 за умови, що 2 є примітивним
елементом поля
за умови, що 2 є примітивним
елементом поля  . Цей
метод також вимагає об'єму обчислень порядку
. Цей
метод також вимагає об'єму обчислень порядку 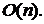
Розглянуті дві частки випадку
оцінюються максимальною складністю у зв'язку з тим, що при переборі всіх точок
криптосистеми колізія виникає лише один раз.
Перехід до псевдовипадкового
алгоритму породжує множина можливих точок колізій, число яких оцінюється як 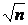 , а обчислювальна складність
методу
, а обчислювальна складність
методу  -Полларда,
застосованого до групи загальної структури, дорівнює
-Полларда,
застосованого до групи загальної структури, дорівнює 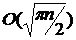 . Оскільки в групі точок EK зворотні точки визначаються досить просто, об'єм
пошуку в просторі точок скорочується вдвічі, а обчислювальна складність
зменшується в
. Оскільки в групі точок EK зворотні точки визначаються досить просто, об'єм
пошуку в просторі точок скорочується вдвічі, а обчислювальна складність
зменшується в 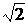 раз і
стає рівною
раз і
стає рівною 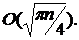
На практиці для виявлення колізій
замість методу Флойда знайшла застосування його модифікація, запропонована
Шнором і Ленстрой. У цієї модифікації пам'ять містить 8 осередків, зрушення
вмісту яких здійснюється при  , де
, де  - номери ітерацій
в останньому й першому осередках відповідно. Отримано експериментальну оцінку
складності цього методу для групи
- номери ітерацій
в останньому й першому осередках відповідно. Отримано експериментальну оцінку
складності цього методу для групи 
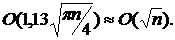
Алгоритм  - методу Полларда з розбивкою на три області
- методу Полларда з розбивкою на три області 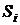 є споконвічним і найбільш
простим у реалізації. Подальші вдосконалення алгоритму пропонують використання
є споконвічним і найбільш
простим у реалізації. Подальші вдосконалення алгоритму пропонують використання 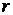 рівноймовірних областей з
вибором, наприклад, ітераційної функції
рівноймовірних областей з
вибором, наприклад, ітераційної функції

Число областей, як правило, не
перевищує 20, тому що подальше їхнє збільшення практично не впливає на
статистичні характеристики алгоритму.
Очевидно колізію точок можна
отримати й іншим шляхом, рухаючись із двох (або більше) різних точок 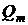 і
і  до збігу
до збігу 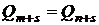 . Ця ситуація відображується на рисунку 2.
Даний метод одержання колізії зветься
. Ця ситуація відображується на рисунку 2.
Даний метод одержання колізії зветься 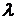 -Методом Полларда. Походження терміна прийнято
з рисунка.
-Методом Полларда. Походження терміна прийнято
з рисунка.
Розглянемо  -метод Полларда на прикладі ЕК
над простим полем Галуа
-метод Полларда на прикладі ЕК
над простим полем Галуа  ,
тобто
,
тобто
криптографичний
дискретний логарифм
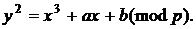 (3)
(3)
Для всіх точок 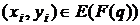 задано операції додавання та подвоєння.
Наприклад, якщо
задано операції додавання та подвоєння.
Наприклад, якщо 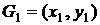 а
а 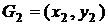 , то
, то
 ,
,

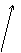




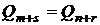

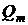

Рисунок 2 - Графічна інтерпретація 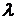 -методу Полларда
-методу Полларда
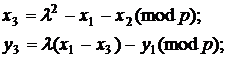
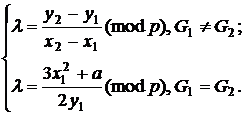 (4)
(4)
Для ЕК над полем  виду
виду
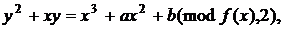
причому  , то для двох точок
, то для двох точок 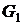 та
та 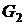 таких, що
таких, що

виходить
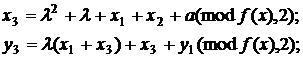 (5)
(5)
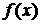 примітивний поліном m-го степеня;
примітивний поліном m-го степеня;
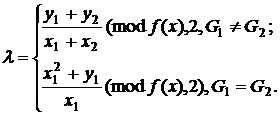 (6)
(6)
Для розв’язання задачі пошуку конфіденційного
ключа  в порівнянні (1)
розглянемо
в порівнянні (1)
розглянемо 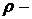 метод
Полларда над простимо полем
метод
Полларда над простимо полем 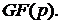 Нехай
Нехай 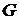 – базова точка,
– базова точка, 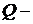 відкритий ключ, шукатимемо пари цілих
відкритий ключ, шукатимемо пари цілих 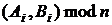 та
та 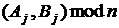 , таких що
, таких що
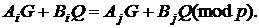 (7)
(7)
Позначимо в загальному вигляді
 (8)
(8)
Суть  -методу Полларда розв’язання порівняння (1)
міститься в наступному. Знайдемо деяку функцію
-методу Полларда розв’язання порівняння (1)
міститься в наступному. Знайдемо деяку функцію  , вибравши
, вибравши 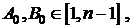 де
де 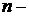 порядок точки
порядок точки 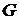 на ЕК
на ЕК
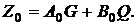 (9)
(9)
Далі знайдемо 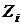 послідовність:
послідовність:
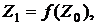
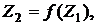
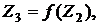 ...,
...,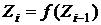
для пар 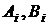 , таких що:
, таких що:
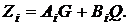 (10)
(10)
Рекомендується в простих випадках
(при відносно невеликих 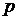 )
послідовність
)
послідовність  розраховувати
у вигляді:
розраховувати
у вигляді:
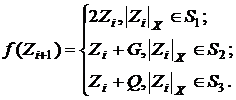 (11)
(11)
При цьому 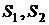 та
та  складають частини області
складають частини області  . Якщо область
. Якщо область  рівномірно ділиться, то (8.11) має
вигляд:
рівномірно ділиться, то (8.11) має
вигляд:
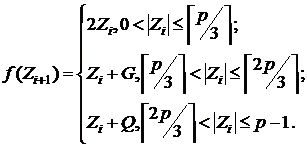 (12)
(12)
При побудові множини 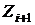 пошук буде успішним, якщо
ми знайдемо
пошук буде успішним, якщо
ми знайдемо
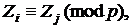
що еквівалентно знаходженню
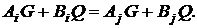 (13)
(13)
Зробивши прості перетворення,
маємо:
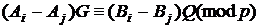 (14)
(14)
і далі
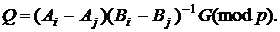 (15)
(15)
З (1) та (15) випливає, що
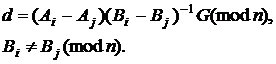 (16)
(16)
Більш ефективним є розрахунок 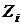 з розбиванням інтервалу
з розбиванням інтервалу 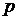 на
на  інтервалів. Для реальних значень
інтервалів. Для реальних значень 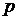 рекомендується
рекомендується 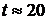 . У цьому випадку замість
(11) маємо
. У цьому випадку замість
(11) маємо
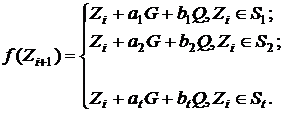 (17)
(17)
причому  та
та  є випадкові цілі із інтервалу
є випадкові цілі із інтервалу 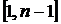 .
.
У випадку (17) розв'язок
знаходиться як і раніше у вигляді (12), а потім (17). З урахуванням позначень в
(17)
 (18)
(18)
Успішне розв'язання задачі
дискретного логарифму в групі точок ЕК вимагає
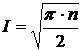 (19)
(19)
операцій на ЕК.
Із (18) та (19) випливає, що
задача пошуку пар  та
та 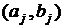 може бути розпаралелено на
може бути розпаралелено на 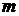 процесорів, тоді
процесорів, тоді
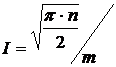 . (20)
. (20)
Розроблено методики та алгоритми,
які дозволяють розв'язати задачу (1) зі складністю
 (21)
(21)
а при розпаралелюванні на 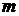 процесорах складність
визначається, як
процесорах складність
визначається, як
 . (22)
. (22)
Під час розв’язання задач важливо
успішно вибрати 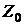 .
Значення
.
Значення 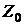 рекомендується
вибирати у вигляді
рекомендується
вибирати у вигляді

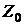 також можна вибрати як
також можна вибрати як
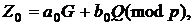
де 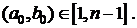
/