Основы теории вероятности

Основы теории вероятности

Контрольная работа

Основы теории вероятности

Задание 1

Проверка выполнимости теоремы Бернулли на примере надёжности электрической схемы.

Формулировка теоремы Бернулли: “Частота появления события в серии  опытов сходится по вероятности к вероятности данного события.”

p₁ = 0.7

p₂ = 0.8

p₃ = 0.9

p₄ = 0.7

p₅ = 0.8

Проверка теоремы с помощью программы:

Текст программы:

Program Cep;

Uses CRT;

Const c=5;

Var op,i,j,n,m:integer;

    a,rab,pp,ppp,ppp1,ppp2:real;

    p:array[1..c] of real;

    x:array[1..c] of byte;

Begin

 ClrScr;

 Randomize;

 p[1]:=0.7; p[2]:=0.8; p[3]:=0.9; p[4]:=0.7; p[5]:=0.8;

 Writeln('    Опытов:   Мсходы:   Вер-ть:'); Writeln;

 For op:=1 to 20 do Begin

   n:=op*100;m:=0;

   Write('    n=',n:4);

   For i:=1 to n do Begin

     For j:=1 to c do Begin

       x[j]:=0;

       a:=random;

       if a<p[j] then x[j]:=1;

     End;

     rab:=x[i]+x[2]*(x[3]+x[4]+x[5]);

     If rab>0 then m:=m+1;

   End;

   pp:=m/n;

   writeln('    M= ',m:4,'   P*= ',pp:3:3);

 End;

 ppp1:=p[1]+p[2]*(p[3]+p[4]+p[5]-p[3]*p[4]-p[3]*p[5]-p[4]*p[5]+p[3]*p[4]*p[5]);

 ppp2:=p[1]*p[2]*(p[3]+p[4]+p[5]-p[3]*p[4]-p[3]*p[5]-p[4]*p[5]+p[3]*p[4]*p[5]);

ppp:=ppp1-ppp2;

Writeln; Writeln('      Вер. в опыте: p=',ppp:6:3);

Readln;

End.

Результаты работы программы

Вер. в опыте: p= 0.939

Проверка в ручную:

Первый способ:

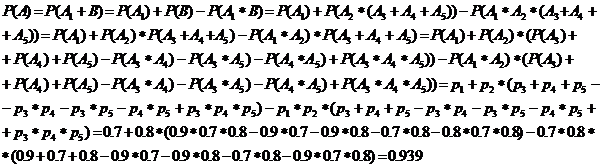
Второй способ:

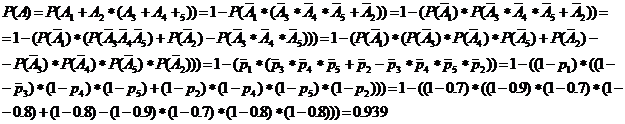
Вывод: Теорема Бернулли верна

Задача № 2

Бросают две игральные кости. Определить вероятность того, что: а) сумма чисел очков не превосходит N; б) произведение числа очков не превосходит N; в)произведение числа очков делится на N. (N = 8)

Исходы:

1-1      2-1      3-1      4-1      5-1      6-1

1-2      2-2      3-2      4-2      5-2      6-2

1-3      2-3      3-3      4-3      5-3      6-3

n = 36 – кол-во комбинаций

1-4      2-4      3-4      4-4      5-4      6-4

1-5      2-5      3-5      4-5      5-5      6-5

1-6      2-6      3-6      4-6      5-6      6-6

а). Сумма чисел не превосходит N = 8 : кол-во благоприятных исходов m = 26

Вероятность

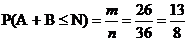
б). Произведение чисел не превосходит N = 8: кол-во благоприятных исходов m = 16

Вероятность

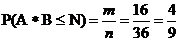
в). Произведение числа очков делится на N = 8 : кол-во благоприятных исходов m = 5

Вероятность

Задача № 3

Имеются изделия четырёх сортов, причём число изделий i - го сорта равно n_i, i = 1, 2, 3, 4.

Для контроля наудачу берутся m – изделий. Определить вероятность того, что среди них m₁ первосортных, m₂, m₃ и m₄ второго, третьего и четвёртого сорта соответственно.

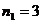
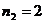
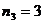
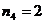
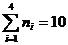
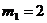
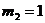
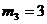
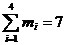
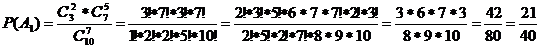
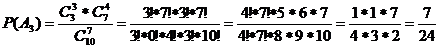
Задача № 4

В лифт k – этажного дома сели n пассажироа (n<k). Каждый независимо от других с одинаковой вероятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что: а) все вышли на разных этажах; б) по крайней мере, двое сошли на одном этаже.

k = 11,  n = 4

а) Все на разных:

n = 11⁴ = 14641

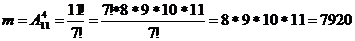
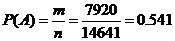
б) Хотя бы два на одном:

Задача № 5

В двух партиях k₁ и k₂% доброкачественных изделий соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них:

а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное.

k₁ = 86% , k₂ = 32%

A₁ - доброкачественные в 1-й партии

A₂ - доброкачественные в 2-й партии

а). одно бракованное:

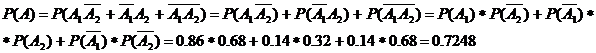
б). два бракованных:

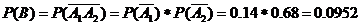
в). Одно доброкачественное и одно бракованное:

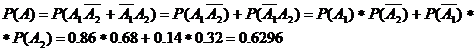
Задача № 6

Из 1000 ламп n_i принадлежат i – партии, i =  1, 2, 3. В первой партии 6%, во второй 5%, в третьей 4% бракованных лам. Наудачу выбирается одна лампа. Определить вероятность того, что выбранная лампа – бракованная.

n₁ = 700         n₂ = 90          n₃ = 210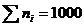         

p₁ = 0.06       p₂ = 0.05       p₃ = 0.04

Пусть:

H₁ – взяли из 1-й партии

H₂ – взяли из 2-й партии

H₃ – взяли из 3-й партии

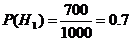
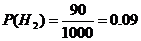
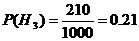
Пусть B_i – брак из i - й партии =>

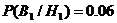
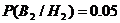
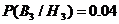
Так как

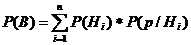 то =>

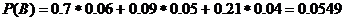
Задача № 7

В альбоме k чистых и l гашёных марок. Из них наудачу извлекаются m марок (среди которых могут быть и чистые и гашёные), подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются n марок. Определить вероятность того, что все n марок чистые.

k = 8, l = 7, m = 3, n = 3

Пусть:

H₁ – все чистые марки

H₂ – 1-чистая, 2-гашёные

H₃ – 2-чистые, 1-гашёная

H₄ – все гашёные

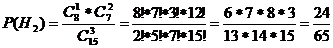
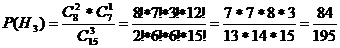
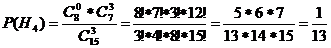
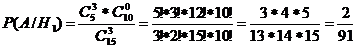
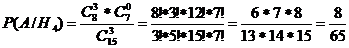
По теореме о полной вероятности:

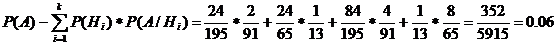
Задача № 8

В магазин поставляют однотипные изделия с трёх заводов, причём i – заводпоставляет m_i% изделий (i = 1, 2, 3). Среди изделий i – го завода n₁% первосортных. Куплено одно изделие.

Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено i – заводом.

m₁ = 60          m₂ = 20          m₃ = 20

n₁ = 70           n₂ = 80           n₃ = 90

Пусть:

H₁ – поставил первый завод

H₂ – поставил второй завод

H₃ – поставил третий завод

Пусть: А – первосортных изделий =>

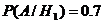
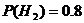
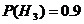
По формуле Бейсса:

 => так как i = 3

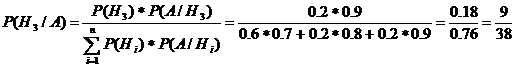
Задача 9

p = 0.3 - вероятность на 1 билет

n = 15 - кол-во купленных билетов

Формула Бернули :

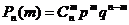
m = 1,2,3,4,…..,n

Производная функция :

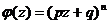
q = 1 – p

Наивероятнейшее число выигравших билетов

  =>

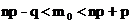
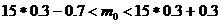
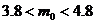Наивероятнейшее число выигравших билетов : m₀ = 4

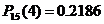 - соответствующая вероятность

Задача № 10

Вероятность “сбоя” в работе телефонной станции при каждом вызове равна p. Поступило n вызовов. Определить вероятность m сбоев.

р = 0.007 - вероятность “сбоя” при вызове

n = 1000 - кол-во вызовов

m = 7 - кол-во “сбоев”

По закону Пуассона:

=>

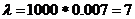
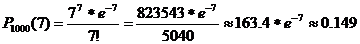
Задача № 11

По данному закону распределения случайной величины найти характеристическую функцию φ(t), математическое ожидание Мξ, дисперсию Dξ случайной величины ξ.

Биномиальный закон:

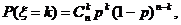
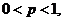
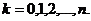
n = 3

p = 0.67

 =>

 =>

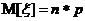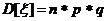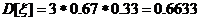
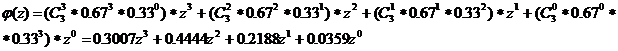
Литература

1.  Е.С. Венцель “Теория вероятности”

2.  В.Ф. Чудесенко “Сборник заданий по спецкурсу высшей математики ТР”

3.  Курс лекций по Теории вероятности