|
x
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
y
|
1
|
1
|
2
|
3
|
5
|
8
|
13
|
21
|
34
|
55
|
|
|
|
|
|
|
|
|
|
|
|
Основные
свойства функции
1) Область определения функции и область значений функции. Область определения функции
- это множество всех допустимых действительных значений аргумента x
(переменной x), при которых функция y = f (x) определена.
Область значений функции - это множество всех действительных значений y,
которые принимает функция. В элементарной математике <#"457111.files/image015.gif">Прямая линия
- график линейной функции y = ax + b. Функция y монотонно возрастает при
a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало
координат т.0 (y = ax - прямая пропорциональность)
 Парабола -
график функции квадратного трёхчлена у = ах2 + bх + с. Имеет
вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 -
максимум. Точки пересечения (если они есть) с осью абсцисс - корни
соответствующего квадратного уравнения ax2 + bx +с =0
Парабола -
график функции квадратного трёхчлена у = ах2 + bх + с. Имеет
вертикальную ось симметрии. Если а > 0, имеет минимум, если а < 0 -
максимум. Точки пересечения (если они есть) с осью абсцисс - корни
соответствующего квадратного уравнения ax2 + bx +с =0
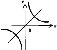 Гипербола -
график функции
Гипербола -
график функции  . При а > О расположена в I и III четвертях, при а
< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а
> 0) или у - х (а < 0).
. При а > О расположена в I и III четвертях, при а
< 0 - во II и IV. Асимптоты - оси координат. Ось симметрии - прямая у = х (а
> 0) или у - х (а < 0).
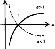 Логарифмическая функция y = logax (a > 0)
Логарифмическая функция y = logax (a > 0)
Тригонометрические
функции. При построении
тригонометрических функций мы используем радианную меру измерения углов.
Тогда функция y = sin x представляется графиком (рис. 19). Эта кривая
называется синусоидой.
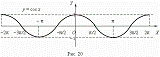
 График функции y = cos x представлен на
рис. 20; это также синусоида, полученная в результате перемещения графика y
= sin x вдоль оси Х влево на
График функции y = cos x представлен на
рис. 20; это также синусоида, полученная в результате перемещения графика y
= sin x вдоль оси Х влево на  /2.
/2.
Основные свойства функций.
Монотонность, четность, нечетность, периодичность функций.
Область определения
функции и область значений функции. Область
определения функции - это множество всех допустимых действительных значений
аргумента x (переменной x), при которых функция y = f (x) определена.
Область значений функции - это множество всех действительных значений y,
которые принимает функция.
В элементарной математике
<#"457111.files/image024.gif">0) и
рис.14 (n < 0). Отрицательные значения x здесь не
рассматриваются, так как тогда некоторые функции:
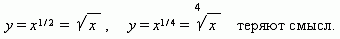
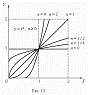 .
.
Обратная
функция
Обра́тная фу́нкция - функция
<#"457111.files/image027.gif">является обратной к функции  , если выполнены следующие тождества:
, если выполнены следующие тождества: 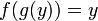 для всех
для всех 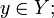
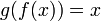 для всех
для всех 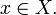
Корень n-ой степени и его
свойства.
Корнем n-ой степени из числа
a называется такое число, n-ая степень которого равна a.
Определение: Арифметическим
корнем n-ой степени из числа a называют неотрицательное число, n-ая степень
которого равна a.
Основные свойства корней:

Степень с произвольным
действительным показателем и его свойства.
Пусть дано положительное
число 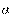 и произвольное действительное число
и произвольное действительное число 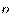 . Число
. Число 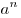 называется
степенью, число
называется
степенью, число 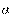 - основанием степени, число
- основанием степени, число 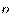 - показателем степени.
- показателем степени.
По определению полагают:
 .
.
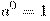 .
.
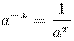 ,
,  .
.
Если 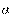 и
и  -
положительные числа,
-
положительные числа, 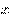 и
и 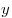 - любые
действительные числа, то справедливы следующие свойства:
- любые
действительные числа, то справедливы следующие свойства:
 .
.
 .
.
 .
.
 .
.
 .
.
 .
.

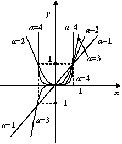
Степенная
функции, её свойства и графики
Степенная функция комплексного переменного f (z) = zn с целочисленным
показателем определяется с помощью аналитического
продолжения
<#"457111.files/image050.gif">, 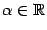 .
Рассматриваются такие случаи:
.
Рассматриваются такие случаи:
а). Если 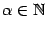 , то
, то  . Тогда
. Тогда  ,
,  ; если
число
; если
число 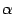 - чётное, то и функция
- чётное, то и функция 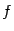 - чётная
(то есть
- чётная
(то есть 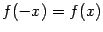 при всех
при всех 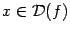 ); если
число
); если
число 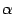 - нечётное, то и функция
- нечётное, то и функция 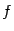 - нечётная (то есть
- нечётная (то есть 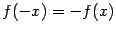 при
всех
при
всех 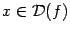 ).
).
Показательная
функция, её свойства и графики
Показательная функция - математическая функция
<#"457111.files/image062.gif">.
В вещественном случае
основание степени 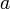 - некоторое неотрицательное вещественное
число
<#"457111.files/image064.gif">;
- некоторое неотрицательное вещественное
число
<#"457111.files/image064.gif">;  ;
; 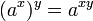 .
.
Показательные
уравнения.
Перейдем непосредственно к
показательным уравнениям. Для того чтобы решить показательное уравнение
необходимо воспользоваться следующей теоремой: Если степени равны и основания
равны, положительны и отличны от единицы, то равны и их показатели степеней.
Докажем эту теорему: Пусть a>1 и aх=ay.
Докажем, что в этом случае
х=y. Допустим противное тому, что требуется доказать, т.е. допустим, что x>у
или что x<у. Тогда получим по свойству показательной функции, что либо aх<ay
либо aх>ay. Оба эти результата противоречат условию
теоремы. Следовательно, x=у, что и требовалось доказать.
Также доказывается теорема и
для случая, когда 0<a<1. Замечание. Из равенства aх=ay
не обязательно следует что x=у. Из равенства 1х=1y также
не обязательно вытекает равенство x=у. Самым простым показательным уравнением
является уравнения вида aх=ay, где a>0 и a≠1.
Показательные
неравенства
Неравенства вида (или меньше) при а (х) >0 и решаются на
основании свойств показательной функции: для 0 < а (х) < 1 при
сравнении f (x) и g (x) знак неравенства меняется, а при а (х)
> 1 - сохраняется. Самый сложный случай при а (х) < 0. Здесь
можно дать только общее указание: определить, при каких значениях х
показатели f (x) и g (x) будут целыми числами, и выбрать из них
те, которые удовлетворяют условию. Наконец, если исходное неравенство будет
выполняться при а (х) = 0 или а (х) = 1 (например, когда
неравенства нестрогие), то нужно рассмотреть и эти случаи.
Логарифмы
и их свойства
Логарифм числа b по основанию a (от греч.
<#"457111.files/image067.gif">. Из определения следует, что записи 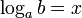 и
и 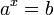 равносильны.
Пример:
равносильны.
Пример: 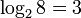 , потому что
, потому что 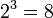 . Свойства
. Свойства
Основное логарифмическое
тождество: 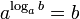
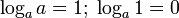
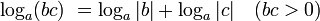
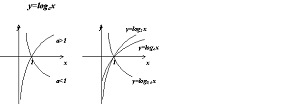
Логарифмическая функция, её
свойства и графики.
Логарифмической функцией
называется функция вида f (x) = logax, определённая
при 
Область определения: 
Область значения: 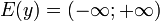
График любой логарифмической
функции проходит через точку (1; 0)
Производная логарифмической
функции равна:

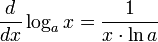
Логарифмические
уравнения
Уравнение, содержащее переменную под знаком логарифма, называется
логарифмическим. Простейшим примером логарифмического уравнения служит
уравнение loga х = b (где а > 0, а 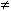 1). Его решение x = ab.
1). Его решение x = ab.
Решение уравнений на основании определения логарифма, например, уравнение
loga х = b (а > 0, а 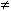 1) имеет решение х = аb.
1) имеет решение х = аb.
Метод потенцирования. Под потенцированием понимается переход от
равенства, содержащего логарифмы, к равенству, не содержащему их:
если loga f (х) = loga g (х), то f (х) =
g (х), f (х) >0, g (х) >0, а > 0, а 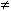 1.
1.
Метод приведения логарифмического уравнения к квадратному.
Метод логарифмирования обеих частей уравнения.
Метод приведения логарифмов к одному и тому же основанию.
Логарифмические неравенства.
Неравенство, содержащее переменную только под знаком логарифма,
называется логарифмическим: loga f (х) > loga g
(х).
При решении логарифмических неравенств следует учитывать общие свойства
неравенств, свойство монотонности логарифмической функции и область ее
определения. Неравенство loga f (х) > loga g (х) равносильно
системе f (x) > g (x) > 0 при a > 1 и системе 0 < f (x)
< g (x) при 0 < а < 1.
Радианное измерение углов и дуг. Синус, косинус, тангенс, котангенс.
Градусная мера. Здесь единицей измерения является градус (обозначение )
- это поворот луча на 1/360 часть одного полного оборота. Таким образом,
полный оборот луча равен 360. Один градус состоит из 60 минут (их
обозначение ‘); одна минута - соответственно из 60 секунд (обозначаются
“).
Радианная мера. Как мы знаем из планиметрии (см. параграф "Длина
дуги" в разделе "Геометрическое место точек. Круг и
окружность"), длина дуги l, радиус r и соответствующий
центральный угол 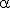 связаны соотношением:
связаны соотношением: 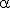 = l / r.
= l / r.
Эта формула лежит в основе определения радианной меры измерения углов.
Так, если l = r, то 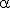 = 1, и мы говорим, что угол
= 1, и мы говорим, что угол 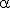 равен 1 радиану, что
обозначается:
равен 1 радиану, что
обозначается: 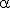 = 1 рад. Таким образом, мы имеем следующее определение
радианной меры измерения:
= 1 рад. Таким образом, мы имеем следующее определение
радианной меры измерения:
Радиан есть центральный угол, у которого длина дуги и радиус
равны (AmB = AO, рис.1). Итак, радианная мера измерения угла есть
отношение длины дуги, проведенной произвольным радиусом и заключённой между
сторонами этого угла, к радиусу дуги.

Тригонометрические функции острых углов можно определить как отношение
длин сторон прямоугольного треугольника.
Синус:

Косинус:
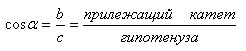
Тангенс:
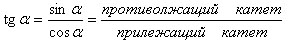
Котангенс:
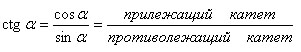
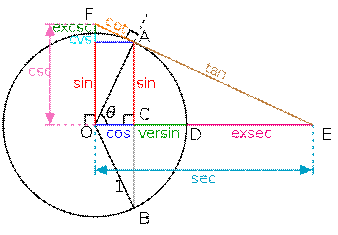
Тригонометрические
функции числового аргумента
Определение.
Формулы сложения. Формулы
двойного и половинного аргумента.
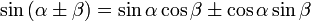

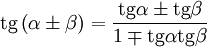
Двойного.
 ;
; 
(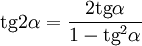 ;
; 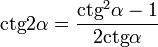 .
.
Тригонометрические функции и
их графики. Основные свойства тригонометрических функций.
Тригонометрические функции - вид элементарных функций
<#"457111.files/image097.gif">
5. Точки пересечения с осями координат:
с осью Ох: sinx = 0; х = pn, nÎZ;
с осью Oy: если х = 0, то у = 0,6. Промежутки
знакопостоянства:
sinx > 0, если xÎ (2pn; p +
2pn), nÎZ;
sinx < 0, если хÎ (p + 2pn; 2p+pn), nÎZ.
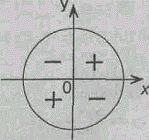
Знаки синуса в четвертях
у > 0 для углов а первой и второй четвертей.
у < 0 для углов ее третьей и четвертой четвертей.
7. Промежутки монотонноти:
y = sinx возрастает
на каждом из промежутков [-p/2 + 2pn; p/2
+ 2pn],
nÎz и
убывает на каждом из промежутков [p/2 + 2pn; 3p/2
+ 2pn], nÎz.
8. Точки экстремума и экстремумы функции:
xmax = p/2 + 2pn, nÎz; ymax =
1;
ymax = - p/2 + 2pn, nÎz; ymin =
- 1.
Свойства функции у = cosx и ее график:
Свойства:
1. D (y) = R.
2. Е (у) = [-1; 1].
3. Функция у = cosx - четная, так как по определению косинуса тригонометрического угла cos (-a) = x/R = cosa на тригонометрическом круге (рис)
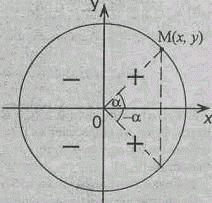
4. Т = 2p - наименьший
положительный период. Действительно,
cos (x+2pn) = cosx.
5. Точки пересечения с осями координат:
с осью Ох: cosx = 0;
х = p/2
+ pn, nÎZ;
с осью Оу: если х = 0,то у = 1.
6. Промежутки знакопостоянства:
cosx > 0, если хÎ (-p/2+2pn; p/2 + 2pn), nÎZ;
cosx < 0, если хÎ (p/2
+ 2pn; 3p/2 + 2pn), nÎZ.
Доказывается это на тригонометрическом круге (рис). Знаки косинуса в
четвертях:
x >
0 для углов a первой и
четвертой четвертей.
x <
0 для углов a второй и
третей четвертей.
7. Промежутки монотонноти:
y = cosx возрастает
на каждом из промежутков [-p + 2pn; 2pn],
nÎz и
убывает на каждом из промежутков [2pn; p + 2pn], nÎz.
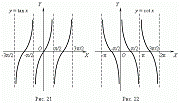
Свойства функции у = tgx и ее график: свойства -
1. D (y) = (xÎR, x ¹ p/2 + pn, nÎZ).
2. E (y) =R.
3. Функция y = tgx -
нечетная
4. Т = p - наименьший
положительный период.
5. Промежутки знакопостоянства:
tgx > 0 при хÎ (pn; p/2 + pn;), nÎZ;
tgx < 0 при xÎ (-p/2 + pn; pn), nÎZ.
Знаки тангенса по четвертям смотри на рисунке.
6. Промежутки монотонности:
y = tgx возрастает
на каждом из промежутков
(-p/2
+ pn; p/2 + pn),
nÎz.
7. Точки экстремума и экстремумы функции:
нет.
8. x = p/2 + pn, nÎz - вертикальные асимптоты
Свойства функции у = ctgx и ее график:
Свойства:
1. D (y) = (xÎR, x ¹ pn, nÎZ). 2. E (y) =R.
3. Функция y = ctgx - нечетная.
4. Т = p - наименьший
положительный период.
5. Промежутки знакопостоянства:
ctgx > 0 при хÎ (pn; p/2 + pn;), nÎZ;
ctgx < 0 при хÎ (-p/2 + pn; pn), nÎZ.
Знаки котангенса по четвертям смотри на рисунке.
7. Точек экстремума и экстремумов у функции у = ctgx нет.
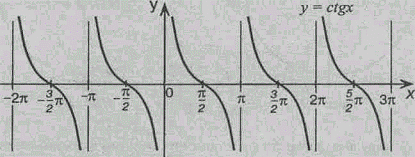
8. Графиком функции у = ctgx является тангенсоида,
полученная сдвигом графика y= tgx вдоль оси Ох влево на p/2 и умножением на (-1) (рис)
Обратные
тригонометрические функции, их свойства и графики
Обра́тные тригонометри́ческие фу́нкции (круговые
функции, аркфункции) - математические
функции
<#"457111.files/image101.gif">
Функция y=arcsinX, её
свойства и графики.
Арксинусом числа m называется такой угол x, для
которого Функция y = sinx непрерывна и ограничена на всей своей
числовой прямой. Функция y = arcsinx является строго возрастающей.
Функция y = sinx непрерывна и ограничена на всей своей
числовой прямой. Функция y = arcsinx является строго возрастающей. 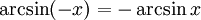 (функция является нечётной
<#"457111.files/image105.gif">
(функция является нечётной
<#"457111.files/image105.gif">
Функция
y=arccosX, её свойства и графики.
Арккосинусом числа m называется такой угол x, для
которого 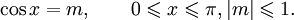
Функция y = cosx
непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx
является строго убывающей. cos (arccosx) = x
при 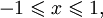 arccos (cosy) = y
при
arccos (cosy) = y
при  D (arccosx) = [− 1; 1], (область
определения), E
(arccosx) = [0; π]. (область
значений). Свойства функции arccos
D (arccosx) = [− 1; 1], (область
определения), E
(arccosx) = [0; π]. (область
значений). Свойства функции arccos (функция центрально-симметрична относительно точки
(функция центрально-симметрична относительно точки 
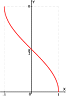
Функция y=arctgX,
её свойства и графики.
Арктангенсом числа m называется такой угол α, для которого  Функция
Функция 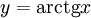 непрерывна и ограничена на всей своей числовой прямой.
Функция
непрерывна и ограничена на всей своей числовой прямой.
Функция 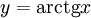 является строго возрастающей.
является строго возрастающей.
 при
при

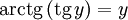 при
при 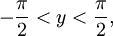
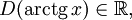
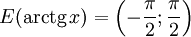
Свойства функции arctg
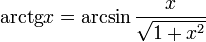 ,
,
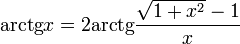 .
.
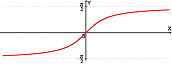
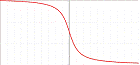
Функция y=arcctg, её свойства и графики.
Арккотангенсом числа m называется такой угол x, для которого 
Функция  непрерывна и ограничена на всей своей числовой прямой.
непрерывна и ограничена на всей своей числовой прямой.
Функция  является строго убывающей.
является строго убывающей. 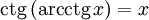 при
при 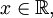
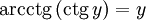 при 0 < y < π
при 0 < y < π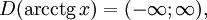
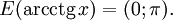 Свойства функции arcctg
Свойства функции arcctg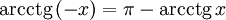 (график функции
центрально-симметричен относительно точки
(график функции
центрально-симметричен относительно точки 
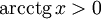 при любых x.
при любых x.
 .
.
Простейшие тригонометрические уравнения.
Определение. Уравнения вада sin x = a; cos x = a; tg x =
a; ctg x = a, где x - переменная, a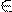 R, называются простейшими
тригонометрическими уравнениями.
R, называются простейшими
тригонометрическими уравнениями.
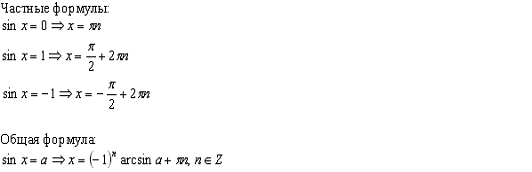


Частные
случаи тригонометрических уравнений
Определение. Уравнения вада sin x = a; cos x = a; tg x =
a; ctg x = a, где x - переменная, a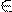 R, называются простейшими
тригонометрическими уравнениями.
R, называются простейшими
тригонометрическими уравнениями.
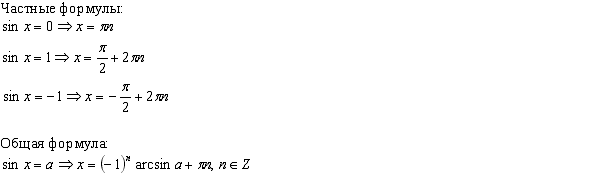
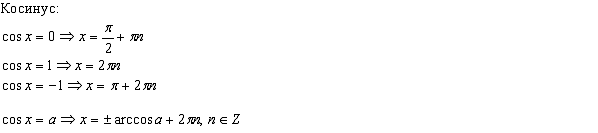

Тригонометрические
уравнения

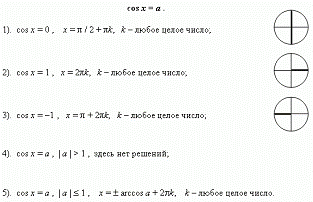

Аксиомы
стереометрии и следствия из них
Основные фигуры в пространстве: точки, прямые и плоскости. Основные
свойства точек, прямых и плоскостей, касающиеся их взаимного расположения,
выражены в аксиомах.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и
притом только одна. А2. Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости
|
|
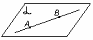
АB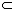  Прямая АВ лежит в
плоскости Прямая АВ лежит в
плоскости 
|
|
рис.5
|
|
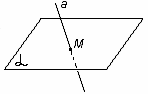
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят,
что они пересекаются.
|
|
а 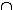  = М Прямая а и плоскость = М Прямая а и плоскость  пересекаются в точке М. пересекаются в точке М.
|
|
Рис.6
|
|
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на
которой лежат все общие точки этих плоскостей.
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и
притом только одна. Следствие 2. Через две пересекающиеся прямые
проходит плоскость, и притом только одна.
Взаимное
расположение двух прямых в пространстве
Две прямые, заданные уравнениями
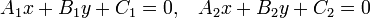 или
или
 пересекаются в точке.
пересекаются в точке.
Параллельность прямой и плоскости.
Определение 2.3 Прямая и плоскость называются параллельными,
если они не имеют общих точек. Если прямая a параллельна
плоскости α, то пишут a || α. Теорема 2.4 Признак
параллельности прямой и плоскости. Если прямая вне плоскости параллельна
какой-нибудь прямой на плоскости, то эта прямая параллельна и самой плоскости.
Доказательство Пусть b 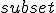 α, a || b и
a
α, a || b и
a 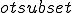 α (чертеж 2.2.1). Доказательство
проведем от противного. Пусть a не параллельна
α,
тогда прямая a пересекает плоскость α
в некоторой точке A. Причем A
α (чертеж 2.2.1). Доказательство
проведем от противного. Пусть a не параллельна
α,
тогда прямая a пересекает плоскость α
в некоторой точке A. Причем A  b,
так как a || b. Согласно
признаку скрещивающихся прямых прямые a и b скрещивающиеся. Мы пришли к противоречию. Теорема
2.5 Если плоскость β проходит через прямую a,
параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a. Доказательство Действительно, прямые a и b не являются
скрещивающимися, так как они лежат в плоскости β. Кроме того, эти прямые не имеют
общих точек, так как a || α. Определение 2.4 Прямую b иногда называют следом
плоскости β на плоскости α.
b,
так как a || b. Согласно
признаку скрещивающихся прямых прямые a и b скрещивающиеся. Мы пришли к противоречию. Теорема
2.5 Если плоскость β проходит через прямую a,
параллельную плоскости α, и пересекает эту плоскость по прямой b, то b || a. Доказательство Действительно, прямые a и b не являются
скрещивающимися, так как они лежат в плоскости β. Кроме того, эти прямые не имеют
общих точек, так как a || α. Определение 2.4 Прямую b иногда называют следом
плоскости β на плоскости α.
Скрещивающиеся
прямые. Признак скрещивающихся прямых
Прямые называются скрещивающимися при выполнении следующего условия: Если
представить, что одна из прямых принадлежит произвольной плоскости, то другая
прямая будет пересекать эту плоскость в точке, не принадлежащей первой прямой.
Иными словами, две прямые в трёхмерном евклидовом пространстве скрещиваются,
если не существует плоскости, их содержащей. Проще говоря, две прямые в
пространстве, не имеющие общих точек, но не являющиеся параллельными.
Теорема (1): Если одна из двух прямых лежит в некоторой плоскости, а
другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то
эти прямые скрещивающиеся.
Теорема (2): Через каждую из двух скрещивающихся прямых проходит
плоскость, параллельная другой прямой, и притом только одна.
Теорема (3): Если стороны двух углов соответственно сонаправлены, то
такие углы равны.
Параллельность прямых. Свойства параллельных плоскостей.
Параллельными (иногда -
равнобежными) прямыми называются прямые
<#"457111.files/image155.gif"> <#"457111.files/image156.gif"> <#"457111.files/image157.gif"> AB - перпендикуляр к плоскости α.
AC - наклонная, CB -
проекция.
С - основание наклонной, B -
основание перпендикуляра.
Угол между прямой и
плоскостью.
Углом между прямой и
плоскостью называется любой угол
между прямой и ее проекцией на эту плоскость.
Двугранный угол.
Двугранный угол - пространственная геометрическая фигура,
образованная двумя полуплоскостями, исходящими из одной прямой, а также часть
пространства, ограниченная этими полуплоскостями. Полуплоскости называются гранями
двугранного угла, а их общая прямая - ребром. Двугранные углы измеряются
линейным углом, то есть углом, образованным пересечением двугранного угла с
плоскостью, перпендикулярной к его ребру. У всякого многогранника, правильного
или неправильного, выпуклого или вогнутого, есть двугранный угол на каждом
ребре.
Перпендикулярность двух
плоскостей.
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ
ПЛОСКОСТЕЙ.
Если плоскость проходит через
прямую перпендикулярную другой плоскости
<http://schools.keldysh.ru/sch1905/Geom_perpendikularnost/prpl.htm>,
то эти плоскости перпендикулярны.