Правила дефферинцирования
Правила дефферинцирования
Самостоятельная работа по
дисциплине: «Математика» Лапшина Дмитрия Петровича студента I курса группы 10п
Новокуйбышевский государственный
гуманитарно-технологический колледж
2010
Основные правила дифференцирования
Обозначим
f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u
v) = u v
2) (uv)
= uv + uv
3)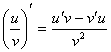 , если v
0
, если v
0
Эти
правила могут быть легко доказаны на основе теорем о пределах.
Производные
основных элементарных функций:
1)С
= 0; 9) 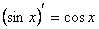
2)(xm)
= mxm-1; 10) 
3)
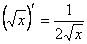 11)
11) 
4)
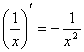 12)
12) 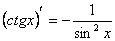
5)
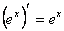 13)
13) 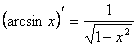
6)
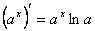 14)
14) 
7) 15)
15) 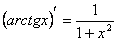
8)
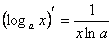 16)
16) 
Логарифмическое
дифференцирование
Дифференцирование
многих функций упрощается, если их предварительно прологарифмировать. Для этого
поступают следующим образом. Если требуется найти y' из уравнения y=f(x), то
можно:
Прологарифмировать
обе части уравнения (по основанию е) ln y = ln f(x) = j(x).
Продифференцировать
обе части равенства, считая ln y сложной функцией от переменной x: 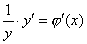 .
.
Выразить
y' = y·j'(x) = f(x)·(lnx)'.
Примеры.
y
= xa - степенная функция с произвольным показателем.
 .
.

Показательно-степенная
функция и ее дифференцирование
Показательно-степенной
функцией называется функция вида y = uv, где u=u(x), v=v(x).
Логарифмическое
дифференцирование применяется для нахождения производной от
показательно-степенной функции.
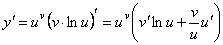

Примеры
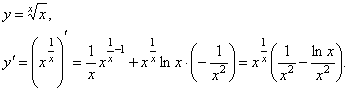
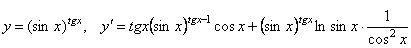 .
.
Таблица
производных
Объединим
в одну таблицу все основные формулы и правили дифференцирования, выведенные
ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных
элементарных функций будем пользоваться теоремой о производной сложной функции.
 .
.
 .
.
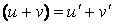 .
.
 .
.
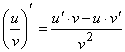 .
.
а)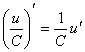 .
.
б)
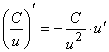 .
.
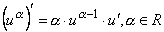 .
.
 .
.
 .
.
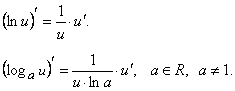
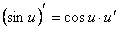 .
.
 .
.
 .
.
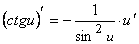 .
.
 .
.
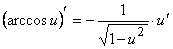 .
.
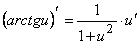 .
.
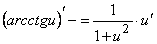 .
.
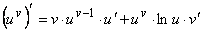 .
.
Примеры


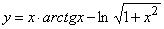 . Найти
y'(-1).
. Найти
y'(-1).

Производная
обратных функций
Пусть
требуется найти производную функции у = f(x) при условии, что обратная ей
функция x = g(y) имеет производную, отличную от нуля в соответствующей точке.
Для
решения этой задачи дифференцируем функцию x = g(y) по х:

т.к.
g(y) 0 

т.е.
производная обратной функции обратна по величине производной данной функции.
Функция
arctg является функцией, обратной функции tg, т.е. ее производная может быть
найдена следующим образом:

Известно,
что 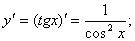
По
приведенной выше формуле получаем:

Т.к.
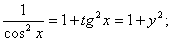 то можно
записать окончательную формулу для производной арктангенса:
то можно
записать окончательную формулу для производной арктангенса:

Понятие
дифференциала функции. Связь между дифференциалом и производной
Пусть
функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в
некоторой точке х0 [a; b] определяется равенством
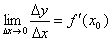
Следовательно,
по свойству предела

Умножая
все члены полученного равенства на Δx, получим:
Δy
= f '(x0)·Δx
+ a·Δx.
Итак,
бесконечно малое приращение Δy дифференцируемой функции y=f(x)
может быть представлено в виде суммы двух слагаемых, из которых первое есть
(при f '(х0) ≠ 0) главная часть приращения, линейная относительно Δx, а второе -
бесконечно малая величина более высокого порядка, чем Δx. Главную
часть приращения функции, т.е. f '(х0)·Δx называют дифференциалом
функции в точке х0 и обозначают через dy.
Таким
образом, если функция y=f(x) имеет производную f '(x) в точке x, то
произведение производной f '(x) на приращение Δx аргумента
называют дифференциалом функции и обозначают:
Найдем
дифференциал функции y= x. В этом случае y' = (x)' = 1 и, следовательно, dy=dx=Δx. Таким
образом, дифференциал dxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому
формулу (1) мы можем записать так:
Но
из этого соотношения следует, что  . Следовательно, производную f '(x)
можно рассматривать как отношение дифференциала функции к дифференциалу
независимой переменной.
. Следовательно, производную f '(x)
можно рассматривать как отношение дифференциала функции к дифференциалу
независимой переменной.
Ранее
мы показали, что из дифференцируемости функции в точке следует существование
дифференциала в этой точке.
Справедливо
и обратное утверждение.
Если
для данного значения x приращение функции Δy = f(x+Δx) - f(x) можно
представить в виде Δy
= A·Δx + α,
где α
- бесконечно
малая величина, удовлетворяющая условию  , т.е. если для функции y=f(x)
существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет
производную в точке x и f '(x)=А.
, т.е. если для функции y=f(x)
существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет
производную в точке x и f '(x)=А.
Действительно,
имеем  , и так как
, и так как 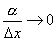 при Δx→0, то
при Δx→0, то  .
.
Таким
образом, между дифференцируемостью функции и существованием дифференциала
имеется очень тесная связь, оба понятия равносильны.
Примеры.
Найти дифференциалы функций:
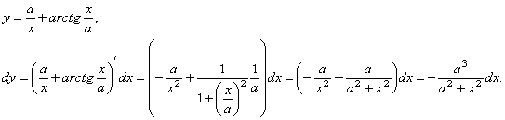
 .
.
Геометрический
смысл дифференциала

Рассмотрим
функцию y=f(x) и соответствующую ей кривую. Возьмем на кривой произвольную
точку M(x; y), проведем касательную к кривой в этой точке и обозначим через α угол,
который касательная образует с положительным направлением оси Ox. Дадим
независимой переменной x приращение Δx, тогда функция получит
приращение Δy
= NM1. Значениям
x+Δx
и
y+Δy
на
кривой y = f(x) будет соответствовать точка
M1(x+Δx;
y+Δy).
Из
ΔMNT
находим
NT=MN·tg α.
Т.к.
tg α
= f '(x),
а MN = Δx, то NT = f
'(x)·Δx.
Но
по определению дифференциала dy=f '(x)·Δx, поэтому dy = NT.
Таким
образом, дифференциал функции f(x), соответствующей данным значениям x и Δx, равен
приращению ординаты касательной к кривой y=f(x) в данной точке х.
Теорема
об инвариантности дифференциала
Ранее
мы видели, что если u является независимой переменной, то дифференциал функции
y=f '(u) имеет вид dy = f '(u)du.
Покажем,
что эта форма сохраняется и в том случае, когда u является не независимой
переменной, а функцией, т.е. найдем выражение для дифференциала сложной
функции. Пусть y=f(u), u=g(x) или y = f(g(x)). Тогда по правилу
дифференцирования сложной функции:
 .
.
Следовательно,
по определению
 ,
,
но
g'(x)dx= du, поэтому dy= f'(u)du.
Мы
доказали следующую теорему.
Теорема.
Дифференциал сложной функции y=f(u), для которой u=g(x), имеет тот же вид
dy=f'(u)du, какой он имел бы, если бы промежуточный аргумент u был независимой
переменной.
Иначе
говоря, форма дифференциала не зависит от того, является аргумент функции
независимой переменной или функцией другого аргумента. Это свойство
дифференциала называется инвариантностью формы дифференциала.
Пример.
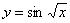 . Найти dy.
. Найти dy.
Учитывая
свойство инвариантности дифференциала, находим
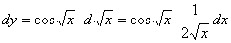 .
.
Применение
дифференциала к приближенным вычислениям
Пусть
нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке
x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как
мы уже выяснили приращение функции Δyможно представить в виде
суммы Δy=dy+α·Δx, т.е.
приращение функции отличается от дифференциала на величину бесконечно малую.
Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных
вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
Т.к.,
по определению, Δy
= f(x) - f(x0),
то f(x) - f(x0)≈f'(x0)·Δx.
Откуда
Примеры:
y = x2 - 2x.
Найти приближенно, с помощью дифференциала, изменение y (т.е. Δy), когда x
изменяется от 3 до 3, 01.
Имеем Δy≈dy=f'(x)·Δx.
f'(x)=2x - 2
, f'(3)=4, Δx=0, 01.
Поэтому Δy ≈
4·0,
01 = 0, 04.
Вычислить
приближенно значение функции  в точке x = 17.
в точке x = 17.
Пусть
x0= 16.
Тогда
Δx
= x - x0= 17 - 16 = 1,
 ,
,
 .
.
Таким
образом,  .
.
Вычислить
ln 0, 99.
Будем
рассматривать это значение как частное значение функции y=lnx при х=0, 99.
Положим
x0 = 1. Тогда Δx
= - 0,
01, f(x0)=0.
 , f
'(1)=1.Поэтому f(0, 99) ≈ 0 - 0, 01 = - 0, 01.
, f
'(1)=1.Поэтому f(0, 99) ≈ 0 - 0, 01 = - 0, 01.
Список литературы
Гордон В.А.,
Шмаркова Л.И. Краткий курс математики / Учебное пособие. - Орёл: ОрёлГТУ, 2000.
- 96 с.
Демидович
Б.П. Сборник задач и упражнений по математическому анализу: М.: Наука, 1996.
Мордкович
А.Г Алгебра 7-11. 2001-2003г
Для
подготовки данной работы были использованы материалы с сайта <http://www.bibliofond.ru>